Las longitudes de dos lados de un triángulo son 20 mm y 13 mm. ¿Cuál de estas longitudes no puede representar la longitud del tercer lado?
- 35 mm
- 10 cm
- 20 mm
- 45 mm
Solución
En cualquier triángulo, la suma de las longitudes de dos lados debe ser mayor que la longitud del tercer lado.
Dados dos lados con longitudes \(20\, \text{mm}\) y \(13\, \text{mm}\), su suma es:
\[ 20 + 13 = 33 \text{ mm}. \]Por lo tanto, la longitud del tercer lado \(x\) debe cumplir:
\[ x \lt 33 \text{ mm}. \]Ahora verificamos las opciones dadas:
- \(35 \text{ mm} > 33 \text{ mm}\) — no es posible,
- \(10 \text{ cm} = 100 \text{ mm} > 33 \text{ mm}\) — no es posible,
- \(20 \text{ mm} \lt 33 \text{ mm}\) — es posible,
- \(45 \text{ mm} > 33 \text{ mm}\) — no es posible.
Por lo tanto, el tercer lado no puede ser \(35\, \text{mm}\), \(10\, \text{cm}\) o \(45\, \text{mm}\).
ABC es un triángulo isósceles. Encuentra la medida del ángulo \( \angle ABC \).

Solución
La suma de los ángulos en el triángulo \(ABC\) es:
\[ 72^\circ + \angle ACB + \angle ABC = 180^\circ. \]Dado que \(ABC\) es isósceles, los ángulos \(ACB\) y \(ABC\) son iguales:
\[ \angle ACB = \angle ABC. \]Sea \(\angle ABC = x\). Entonces:
\[ 72^\circ + 2x = 180^\circ \implies 2x = 180^\circ - 72^\circ = 108^\circ \implies x = 54^\circ. \]Por lo tanto:
\[ \angle ABC = 54^\circ. \]El perímetro de un triángulo equilátero es 210 cm. ¿Cuál es la longitud de un lado de este triángulo?
Solución
En un triángulo equilátero, todos los lados son iguales. Si la longitud de un lado es \(x\), entonces el perímetro es:
\[ 3x = 210. \]Resolviendo para \(x\):
\[ x = \frac{210}{3} = 70 \text{ cm}. \]Encuentra \(x\) para que el triángulo mostrado sea un triángulo rectángulo.
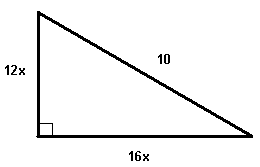
Solución
Usamos el teorema de Pitágoras:
\[ (12x)^2 + (16x)^2 = 10^2. \]Calculamos cada término:
\[ 144 x^2 + 256 x^2 = 100. \]Combinamos términos semejantes:
\[ 400 x^2 = 100. \]Resolvemos para \(x^2\):
\[ x^2 = \frac{100}{400} = \frac{1}{4}. \]Tomamos la raíz positiva (ya que la longitud es positiva):
\[ x = \frac{1}{2}. \]¿Cuáles serán los vértices del triángulo obtenido al reflejar sobre el eje x el triángulo definido por los vértices \((1, 2), (2, -3)\) y \((4, -1)\)?
Solución
Cuando un punto \((x, y)\) se refleja sobre el eje x, la coordenada y cambia de signo, por lo que el punto reflejado es \((x, -y)\).
Así, los vértices reflejados son:
\[ (1, -2), \quad (2, 3), \quad (4, 1). \]Los dos triángulos mostrados son similares. Encuentra la longitud de la hipotenusa del triángulo más grande.

Solución
En triángulos similares, los lados correspondientes son proporcionales. Sea \(h\) la hipotenusa del triángulo pequeño y \(H\) la hipotenusa del triángulo grande. Entonces:
\[ \frac{8}{15} = \frac{h}{H}. \]Usamos el teorema de Pitágoras para encontrar \(h\):
\[ h^2 = 8^2 + 6^2 = 64 + 36 = 100, \] \[ h = 10. \]Sustituimos \(h = 10\) en la proporción:
\[ \frac{8}{15} = \frac{10}{H}. \]Multiplicamos en cruz:
\[ 8H = 150, \] \[ H = \frac{150}{8} = 18.75. \]Una escalera de 13 pies está apoyada contra una pared vertical. El pie de la escalera está a 4 pies de la pared. ¿Cuál es la altura del punto donde la escalera toca la pared? (Redondea tu respuesta a la décima de pie más cercana.)
Solución
La escalera, la pared y el suelo forman un triángulo rectángulo donde la escalera es la hipotenusa de 13 pies y un cateto mide 4 pies. Sea la altura \(x\). Usamos el teorema de Pitágoras:
\[ x^2 + 4^2 = 13^2. \]Resolvemos para \(x^2\):
\[ x^2 = 169 - 16 = 153. \]Calculamos \(x\):
\[ x = \sqrt{153} \approx 12.4 \text{ pies (redondeado a la décima más cercana)}. \]Esta altura \(x\) es el punto donde la escalera toca la pared.
La longitud de la hipotenusa de un triángulo rectángulo es 40 cm. Uno de sus ángulos es \(45^\circ\). ¿Cuáles son las longitudes exactas de los otros dos lados del triángulo?
Solución
En un triángulo rectángulo con un ángulo de \(45^\circ\), el otro ángulo no recto también es \(45^\circ\). Por lo tanto, el triángulo es isósceles y los dos catetos son iguales. Sea cada cateto de longitud \(x\).
Usando el teorema de Pitágoras:
\[ x^2 + x^2 = 40^2, \] \[ 2x^2 = 1600, \] \[ x^2 = 800 = 2 \times 400, \] \[ x = \sqrt{2 \times 400} = 20 \sqrt{2}. \]Por lo tanto, las longitudes de los otros dos lados son \(20 \sqrt{2} \, \text{cm}\) cada una.
El triángulo ABC es isósceles. La longitud de la base es 20 metros y la altura correspondiente es 24 metros. Encuentra el perímetro de ABC. (Redondea tu respuesta a la décima de metro más cercana).
Solución
El triángulo isósceles ABC se muestra a continuación. Se dibuja la altura AM. Los triángulos AMB y AMC son congruentes ya que tienen dos lados congruentes AB y AC, y AM es común. Además, los ángulos B y C son iguales en medida y los ángulos rectos en M son iguales. Por lo tanto, las longitudes de AM y CM son iguales, y la longitud de MC es igual a 10 metros.

Ahora usamos el teorema de Pitágoras para encontrar la longitud \(x\) del lado AB:
\[ x^2 = 24^2 + 10^2 = 576 + 100 = 676 \] \[ x = \sqrt{676} = 26 \text{ metros}. \]El perímetro del triángulo es:
\[ \text{Perímetro} = AB + AC + BC = 26 + 26 + 20 = 72 \text{ metros}. \]Un triángulo tiene un área de 90 cm². Encuentra la longitud de la base si la base es 3 cm más larga que la altura.
Solución
Sea \(b\) la longitud de la base y \(h\) la altura. El área \(A\) del triángulo es:
\[ A = \frac{1}{2} \times b \times h = 90. \]Dado:
\[ b = h + 3. \]Sustituimos \(b = h + 3\) en la fórmula del área:
\[ \frac{1}{2} (h + 3) h = 90. \]Multiplicamos ambos lados por 2:
\[ (h + 3) h = 180. \]Expandimos:
\[ h^2 + 3h = 180. \]Reescribimos como ecuación cuadrática:
\[ h^2 + 3h - 180 = 0. \]Factorizamos:
\[ (h - 12)(h + 15) = 0. \]Entonces:
\[ h = 12 \quad \text{(ya que la altura debe ser positiva)}. \]Calculamos la base:
\[ b = 12 + 3 = 15 \text{ cm}. \]El perímetro de un triángulo es 74 pulgadas. La longitud del primer lado es el doble de la longitud del segundo lado. El tercer lado es 4 pulgadas más largo que el primer lado. Encuentra la longitud de cada lado.
Solución
Sea \(x\) la longitud del segundo lado. Entonces:
\[ \text{Primer lado} = 2x, \] \[ \text{Tercer lado} = 2x + 4. \]El perímetro es:
\[ 2x + x + (2x + 4) = 5x + 4 = 74. \]Resolvemos para \(x\):
\[ 5x = 70, \] \[ x = 14. \]Las longitudes de los lados son:
\[ \text{Lado 1} = 2x = 28 \text{ pulgadas}, \] \[ \text{Lado 2} = x = 14 \text{ pulgadas}, \] \[ \text{Lado 3} = 2x + 4 = 28 + 4 = 32 \text{ pulgadas}. \]Determina el área del triángulo encerrado por las líneas \(y = -4\), \(x = 1\) y \(y = -2x + 8\).
Solución
El triángulo tiene vértices en las intersecciones de las líneas. Para encontrar su área, encontramos las longitudes de la base y la altura localizando los puntos A, B y C.

Encontramos el punto \(A\) intersectando \(x=1\) y \(y=-2x + 8\):
\[ x=1 \implies y = -2(1) + 8 = 6. \] \[ A = (1, 6). \]Encontramos el punto \(B\) intersectando \(y = -4\) y \(y = -2x + 8\):
\[ -4 = -2x + 8 \implies -2x = -12 \implies x = 6. \] \[ B = (6, -4). \]La altura \(AB\) es la distancia vertical:
\[ AB = |6 - (-4)| = 10. \]La base \(BC\) es la distancia horizontal entre \(B\) y \(C\), donde \(C\) está en \(x=1\) y \(y=-4\):
\[ C = (1, -4), \] \[ BC = |6 - 1| = 5. \]El área \(A\) es:
\[ A = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 10 \times 5 = 25 \text{ unidades cuadradas}. \]Demuestra que el triángulo con vértices \(A(-1,6)\), \(B(2,6)\) y \(C(2,2)\) es un triángulo rectángulo y encuentra su área.
Solución
Calculamos las longitudes al cuadrado de los lados:
\[ AB^2 = (2 - (-1))^2 + (6 - 6)^2 = 3^2 + 0^2 = 9, \] \[ BC^2 = (2 - 2)^2 + (2 - 6)^2 = 0^2 + (-4)^2 = 16, \] \[ CA^2 = (-1 - 2)^2 + (6 - 2)^2 = (-3)^2 + 4^2 = 9 + 16 = 25. \]Verificamos el teorema de Pitágoras:
\[ CA^2 = AB^2 + BC^2 \implies 25 = 9 + 16. \]Dado que se cumple la igualdad, el triángulo ABC es rectángulo con hipotenusa \(CA\).
El área \(A\) es:
\[ A = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 3 \times 4 = 6 \text{ unidades cuadradas}. \]