Los ángulos \(A\) y \(B\) son complementarios, y la medida del ángulo \(A\) es el doble de la medida del ángulo \(B\). Encuentra las medidas de los ángulos \(A\) y \(B\).
Solución
Sea \(A\) la medida del ángulo \(A\) y \(B\) la medida del ángulo \(B\). Por lo tanto:
\[ A = 2B \]
Los ángulos \(A\) y \(B\) son complementarios; por lo tanto:
\[ A + B = 90^\circ \]
Pero \(A = 2B\); luego:
\[ 2B + B = 90 \]
\[ 3B = 90 \]
\[ B = \frac{90}{3} = 30^\circ \]
\[ A = 2B = 60^\circ \]
ABCD es un paralelogramo tal que \( AB \parallel DC \) y \( DA \parallel CB \). La longitud del lado \( AB \) es \( 20 \, \text{cm} \). E es un punto entre A y B tal que la longitud de \( AE \) es \( 3 \, \text{cm} \). F es un punto entre los puntos D y C. Encuentra la longitud de \( DF \) tal que el segmento \( EF \) divide el paralelogramo en dos regiones de igual área.
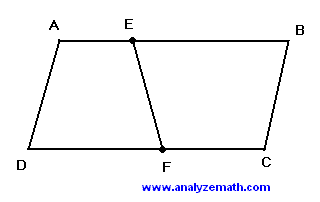
Solución
Sea \( A_1 \) el área del trapecio AEFD. Por lo tanto:
\[ A_1 = \frac{1}{2} h (AE + DF) = \frac{1}{2} h (3 + DF) \]
donde \( h \) es la altura del paralelogramo.
Ahora sea \( A_2 \) el área del trapecio EBCF. Por lo tanto:
\[ A_2 = \frac{1}{2} h (EB + FC) \]
También tenemos:
\[ EB = 20 - AE = 17, \quad FC = 20 - DF \]
Sustituyendo \( EB \) y \( FC \) en \( A_2 \):
\[ A_2 = \frac{1}{2} h (17 + 20 - DF) = \frac{1}{2} h (37 - DF) \]
Para que \( EF \) divida el paralelogramo en dos regiones de igual área, establecemos \( A_1 = A_2 \):
\[ \frac{1}{2} h (3 + DF) = \frac{1}{2} h (37 - DF) \]
Multiplicamos ambos lados por 2 y dividimos por \( h \):
\[ 3 + DF = 37 - DF \]
Resolviendo para \( DF \):
\[ 2DF = 37 - 3 \]
\[ 2DF = 34 \]
\[ DF = 17 \ \text{cm} \]
Encuentra la medida del ángulo \( A \) en la siguiente figura.

Solución
Un primer ángulo interior del triángulo es suplementario al ángulo cuya medida es \( 129^\circ \) y es igual a:
\[ 180^\circ - 129^\circ = 51^\circ \]
Un segundo ángulo interior del triángulo es suplementario al ángulo cuya medida es \( 138^\circ \) y es igual a:
\[ 180^\circ - 138^\circ = 42^\circ \]
La suma de los tres ángulos del triángulo es igual a \( 180^\circ \). Por lo tanto:
\[ A + 51^\circ + 42^\circ = 180^\circ \]
\[ A = 180^\circ - 51^\circ - 42^\circ = 87^\circ \]
ABC es un triángulo rectángulo. AM es perpendicular a BC. El tamaño del ángulo \( \angle ABC \) es igual a \( 55^\circ \). Encuentra el tamaño del ángulo \( \angle MAC \).

Solución
La suma de todos los ángulos en el triángulo \(ABC\) es igual a \(180^\circ\). Por lo tanto:
\[ \angle ABC + \angle ACB + 90^\circ = 180^\circ \]
Sustituyendo \(\angle ABC = 55^\circ\) y resolviendo para \(\angle ACB\):
\[ \angle ACB = 180^\circ - 90^\circ - 55^\circ = 35^\circ \]
La suma de todos los ángulos en el triángulo \(AMC\) es igual a \(180^\circ\). Por lo tanto:
\[ \angle MAC + \angle ACB + 90^\circ = 180^\circ \]
Sustituyendo \(\angle ACB = 35^\circ\) y resolviendo para \(\angle MAC\):
\[ \angle MAC = 180^\circ - 90^\circ - 35^\circ = 55^\circ \]
Encuentra el tamaño del ángulo \( MBD \) en la siguiente figura.

Solución
La suma de todos los ángulos en el triángulo \( AMC \) es igual a \( 180^\circ \). Por lo tanto:
\[ 56 + 78 + \angle AMC = 180 \]
\[ \angle AMC = 180 - 56 - 78 = 46^\circ \]
Los ángulos \( AMC \) y \( DMB \) son opuestos por el vértice y, por lo tanto, iguales en medida. Luego:
\[ \angle DMB = 46^\circ \]
La suma de los ángulos del triángulo \( DMB \) es igual a \( 180^\circ \). Por lo tanto:
\[ \angle MBD + \angle DMB + 62 = 180 \]
Sustituyendo \(\angle DMB = 46^\circ\) y resolviendo para \(\angle MBD\):
\[ \angle MBD + 46 + 62 = 180 \]
\[ \angle MBD = 180 - 46 - 62 = 72^\circ \]
El tamaño del ángulo \(AOB\) es igual a \(132^\circ\) y el tamaño del ángulo \(COD\) es igual a \(141^\circ\). Encuentra el tamaño del ángulo \(DOB\).

Solución
El ángulo \(AOB = 132^\circ\) y también es la suma de los ángulos \(AOD\) y \(DOB\). Por lo tanto:
\[ \angle AOD + \angle DOB = 132^\circ \quad \text{(I)} \]
El ángulo \(COD = 141^\circ\) y también es la suma de los ángulos \(COB\) y \(BOD\). Por lo tanto:
\[ \angle COB + \angle DOB = 141^\circ \quad \text{(II)} \]
Ahora sumamos los lados izquierdos y los lados derechos para obtener una nueva ecuación:
\[ \angle AOD + \angle DOB + \angle COB + \angle DOB = 132 + 141 \quad \text{(III)} \]
Nótese que:
\[ \angle AOD + \angle DOB + \angle COB = 180^\circ \]
Sustituyendo \(\angle AOD + \angle DOB + \angle COB\) en (III) por \(180^\circ\) y resolviendo para \(\angle DOB\):
\[ 180^\circ + \angle DOB = 132^\circ + 141^\circ \]
\[ \angle DOB = 273^\circ - 180^\circ = 93^\circ \]
Encuentra el tamaño del ángulo \(x\) en la figura.
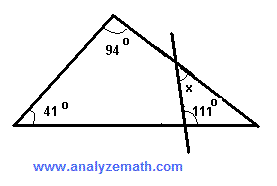
Solución
El ángulo interior del cuadrilátero de la izquierda que es suplementario a \(x\) es igual a:
\[ 180 - x \]
El ángulo interior del cuadrilátero de la izquierda que es suplementario al ángulo de medida \(111^\circ\) es:
\[ 180 - 111 = 69^\circ \]
La suma de todos los ángulos interiores del cuadrilátero es igual a \(360^\circ\). Por lo tanto:
\[ 41 + 94 + (180 - x) + 69 = 360 \]
Resolviendo para \(x\):
\[ 384 - x = 360 \]
\[ x = 384 - 360 = 24^\circ \]
El rectángulo de abajo está formado por 12 cuadrados congruentes (del mismo tamaño). Encuentra el perímetro del rectángulo si el área del rectángulo es igual a \( 432 \) cm².

Solución
Si el área total del rectángulo es \( 432 \ \text{cm}^2 \), el área de un cuadrado es:
\[ \frac{432}{12} = 36 \ \text{cm}^2 \]
Sea \( x \) el lado de un cuadrado pequeño. El área de un cuadrado pequeño es:
\[ x^2 = 36 \]
Resolviendo para \( x \):
\[ x = 6 \ \text{cm} \]
La longitud \( L \) del rectángulo es \( 4x \) y el ancho \( W \) es \( 3x \):
\[ L = 4 \times 6 = 24 \ \text{cm}, \quad W = 3 \times 6 = 18 \ \text{cm} \]
El perímetro \( P \) del rectángulo es:
\[ P = 2(L + W) = 2(24 + 18) = 84 \ \text{cm} \]
ABC es un triángulo rectángulo. El tamaño del ángulo \( \angle ACB \) es igual a \( 74^\circ \). Las longitudes de los segmentos \( AM \), \( MQ \) y \( QP \) son todas iguales. Encuentra la medida del ángulo \( \angle QPB \).
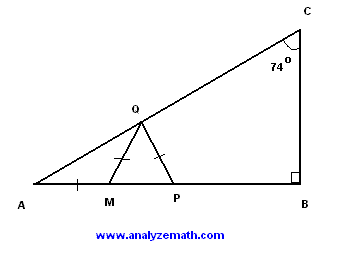
Solución
El ángulo \( CAB \) en el triángulo rectángulo \( ACB \) está dado por:
\[ 90^\circ - 74^\circ = 16^\circ \]
Los lados \( AM \) y \( MQ \) son iguales en longitud, por lo tanto, el triángulo \( AMQ \) es isósceles. Luego:
\[ \angle AQM = \angle QAM = 16^\circ \]
La suma de todos los ángulos interiores en el triángulo \( AMQ \) es igual a \( 180^\circ \). Por lo tanto:
\[ 16^\circ + 16^\circ + \angle AMQ = 180^\circ \]
Resolviendo para \( \angle AMQ \):
\[ \angle AMQ = 180^\circ - 32^\circ = 148^\circ \]
El ángulo \( QMP \) es suplementario al ángulo \( AMQ \). Por lo tanto:
\[ \angle QMP = 180^\circ - \angle AMQ = 180^\circ - 148^\circ = 32^\circ \]
Las longitudes \( QM \) y \( QP \) son iguales; por lo tanto, el triángulo \( QMP \) es isósceles, y así:
\[ \angle QPM = \angle QMP = 32^\circ \]
El ángulo \( QPB \) es suplementario al ángulo \( QPM \). Por lo tanto:
\[ \angle QPB = 180^\circ - \angle QPM = 180^\circ - 32^\circ = 148^\circ \]
Encuentra el área de la figura dada.
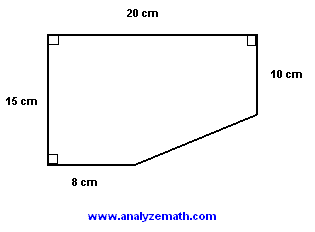
Solución
El área de la figura dada puede encontrarse restando el área del triángulo rectángulo (rojo) del área del rectángulo grande (ver figura abajo).

Los lados del triángulo rectángulo (rojo) son:
\[ 15 - 10 = 5 \text{ cm}, \quad 20 - 8 = 12 \text{ cm} \]
El área de la figura dada es:
\[ \text{Área} = 20 \times 15 - \frac{1}{2} \times 12 \times 5 = 300 - 30 = 270 \text{ cm}^2 \]
Encuentra el área de la región sombreada.

Solución
El área de la figura sombreada puede encontrarse restando el área del rectángulo en la esquina superior izquierda del área del rectángulo grande.
Dimensiones del rectángulo en la esquina superior izquierda:
\[ \text{largo} = 30 - 8 = 22 \text{ cm}, \quad \text{ancho} = 15 - 4 = 11 \text{ cm} \]
Área de la figura sombreada:
\[ \text{Área} = 30 \times 15 - 22 \times 11 = 450 - 242 = 208 \text{ cm}^2 \]
Los vértices del cuadrado inscrito (interior) bisecan los lados del segundo cuadrado (exterior). Encuentra la razón del área del cuadrado exterior al área del cuadrado inscrito.

Solución
Sea \(2x\) la longitud del lado del cuadrado grande (ver figura abajo).

El área del cuadrado grande es:
\[ (2x) \times (2x) = 4x^2 \]
El área del cuadrado inscrito es:
\[ y \times y = y^2 \]
Usando el teorema de Pitágoras para el triángulo rectángulo formado por la mitad del cuadrado grande, obtenemos:
\[ y^2 = x^2 + x^2 = 2x^2 \]
La razón \(R\) del área del cuadrado exterior al área del cuadrado interior es:
\[ R = \frac{4x^2}{y^2} = \frac{4x^2}{2x^2} = \frac{4}{2} = 2 : 1 \]