Problemas de Matemáticas con Soluciones y Explicaciones para 9º Grado

Soluciones detalladas y explicaciones completas para los problemas de matemáticas de 9º grado.

  1. ¿Qué número(s) es/son igual(es) a su(s) propio(s) cuadrado(s)?

    Solución

    Si \(x\) es el número a encontrar, su cuadrado es \(x^{2}\). \(x\) es igual a su cuadrado, por lo tanto:

    \[ x = x^{2} \]

    Resolvemos la ecuación factorizando:

    \[ x - x^{2} = 0 \] \[ x(1 - x) = 0 \]

    Soluciones:

    \[ x = 0 \quad \text{y} \quad x = 1 \]

    Comprobación:

    1) \(x = 0\), su cuadrado es \(0^{2} = 0\). Por lo tanto, \(x\) y su cuadrado son iguales.

    2) \(x = 1\), su cuadrado es \(1^{2} = 1\). Por lo tanto, \(x\) y su cuadrado son iguales.

  2. ¿Qué número(s) es/son igual(es) a la mitad de su(s) cuadrado(s)?

    Solución

    Sea \(x\) el número a encontrar. La mitad de su cuadrado es \(\frac{1}{2} x^2\).

    \[ x = \frac{1}{2} x^2 \]

    Reescribimos:

    \[ x - \frac{1}{2} x^2 = 0 \] \[ x \left( 1 - \frac{1}{2}x \right) = 0 \]

    Soluciones:

    \[ x = 0 \quad \text{y} \quad x = 2 \]

    Comprobación:

    1) \(x = 0\), la mitad de su cuadrado es \(\frac{1}{2} \cdot 0^2 = 0\).

    2) \(x = 2\), la mitad de su cuadrado es \(\frac{1}{2} \cdot 2^2 = 2\).

  3. ¿Qué número(s) es/son igual(es) a la cuarta parte de su(s) cuadrado(s)?

    Solución

    Si \(x\) es el número, la cuarta parte de su cuadrado es \(\frac{1}{4} x^2\).

    \[ x = \frac{1}{4} x^2 \]

    Reescribimos:

    \[ x - \frac{1}{4} x^2 = 0 \] \[ x \left( 1 - \frac{1}{4}x \right) = 0 \]

    Soluciones:

    \[ x = 0 \quad \text{y} \quad x = 4 \]

    Comprobación:

    1) \(x = 0\), la cuarta parte de su cuadrado es \(\frac{1}{4} \cdot 0^2 = 0\).

    2) \(x = 4\), la cuarta parte de su cuadrado es \(\frac{1}{4} \cdot 4^2 = 4\).

  4. Un coche viaja de A a B a 40 mph y regresa por la misma carretera de B a A a 60 mph. ¿Cuál es la velocidad promedio del viaje redondo?

    Solución

    Velocidad promedio = \(\frac{\text{distancia total}}{\text{tiempo total}}\).

    Sea \(x\) la distancia de A a B. Distancia total = \(2x\).

    Tiempo total \(T = \frac{x}{40} + \frac{x}{60} = \frac{x}{24}\).

    Velocidad promedio = \(\frac{2x}{x/24} = 48 \ \text{mph}\).

  5. Tom viaja a 60 mph hacia una ciudad vecina y a 50 mph de regreso por la misma carretera. Condujo un total de 5 horas entre ida y vuelta. ¿Cuál es la distancia desde la casa de Tom hasta la ciudad que visitó? (redondea a la milla más cercana).

    Solución

    Sea \(x\) la distancia. Tiempo de ida: \(\frac{x}{60}\), tiempo de regreso: \(\frac{x}{50}\).

    \[ \frac{x}{60} + \frac{x}{50} = 5 \] \[ \frac{11x}{300} = 5 \] \[ x = \frac{1500}{11} \approx 136 \ \text{millas} \]
  6. A las 11:00 a.m., John comenzó a conducir por una carretera a 50 mph. Un cuarto de hora después, Jimmy comenzó a conducir por la misma carretera en la misma dirección a 65 mph. ¿A qué hora Jimmy alcanzará a John?

    Solución

    Sea \(t\) las horas desde las 11:00 a.m. cuando Jimmy alcanza a John. Jimmy conduce durante \(t - \frac14\) horas.

    Igualamos distancias:

    \[ 50t = 65\left(t - \frac14\right) \] \[ 15t = \frac{65}{4} \] \[ t = \frac{65}{60} \approx 1.083 \ \text{horas} = 1 \ \text{hora} \ 5 \ \text{minutos} \]

    Jimmy alcanza a John a las 12:05 p.m.

  7. Encuentra la ecuación de la recta que pasa por \((-4, 5)\) y es perpendicular a la recta \(5x - 3y = 4\).

    Solución

    Pendiente de la recta dada: \(y = \frac{5}{3}x - \frac{4}{3}\), entonces \(m_{\text{dada}} = \frac{5}{3}\).

    Pendiente de la recta perpendicular: \(m = -\frac{3}{5}\).

    Ecuación:

    \[ y - 5 = -\frac{3}{5}(x + 4) \] \[ 5y + 3x = 13 \]
  8. Un campo rectangular tiene un área de \(300\ \text{m}^2\) y un perímetro de \(80\ \text{m}\). ¿Cuáles son el largo y el ancho del campo?

    Solución

    Sea \(L\) el largo y \(W\) el ancho.

    \[ L \cdot W = 300 \] \[ 2(L + W) = 80 \Rightarrow L + W = 40 \]

    Sustituyendo \(W = 40 - L\):

    \[ L(40 - L) = 300 \] \[ L^2 - 40L + 300 = 0 \] \[ (L - 30)(L - 10) = 0 \]

    Soluciones: \(L = 30\ \text{m}, W = 10\ \text{m}\) (asumiendo \(L > W\)).

  9. Encuentra el área de un trapecio cuyos lados paralelos miden \(12\ \text{cm}\) y \(23\ \text{cm}\).

    Solución

    El área de un trapecio es \(A = \frac{1}{2} h (b_1 + b_2)\).

    Falta la altura \(h\), por lo que no hay suficiente información.

  10. Un jardín rectangular en la casa de la Sra. Dorothy tiene un largo de \(100\ \text{m}\) y un ancho de \(50\ \text{m}\). Se construirá una piscina cuadrada dentro del jardín. Encuentra la longitud de un lado de la piscina si el área restante es igual a la mitad del área del jardín rectangular.

    Solución

    Sea \(x\) el lado de la piscina. Área de la piscina: \(x^2\).

    \[ x^2 = \frac{1}{2} \times (100 \times 50) = 2500 \] \[ x = 50\ \text{m} \]
  11. ABC es un triángulo equilátero con lado igual a \(50\) cm. \(BH\) es perpendicular a \(AC\). \(MN\) es paralela a \(AC\). Encuentra el área del triángulo \(BMN\) si la longitud de \(MN\) es igual a \(12\) cm.

    problema 11

    Solución

    Triángulos \(BMN\) y \(BHC\) son semejantes. La razón de semejanza es \(\frac{12}{25}\).

    Área de \(BHC\): \(B = \frac12 \cdot 25\sqrt{3} \cdot 25 = \frac12 \cdot 25^2 \sqrt{3}\).

    Área de \(BMN\): \(A = \left(\frac{12}{25}\right)^2 \cdot B = 72\sqrt{3} \ \text{cm}^2\).

  12. La altura \(h\) del agua en un recipiente cilíndrico con radio \(r = 5\) cm es igual a \(10\) cm. Peter necesita medir el volumen de una piedra con forma complicada, así que la coloca dentro del recipiente con agua. La altura del agua sube a \(13.2\) cm. ¿Cuál es el volumen de la piedra en cm³?

    problema 12

    Solución

    Volumen inicial: \(V_1 = 10 \cdot (\pi \cdot 5^2) = 250\pi\).

    Volumen final: \(V_2 = 13.2 \cdot (\pi \cdot 5^2) = 330\pi\).

    Volumen de la piedra: \(V_2 - V_1 = 80\pi \approx 251.1 \ \text{cm}^3\).

  13. En la figura, el cuadrado tiene todos sus vértices en la circunferencia. El área del cuadrado es \(400\) cm². ¿Cuál es el área de la forma circular?

    problema 13

    Solución

    Lado del cuadrado: \(x = 20\) cm. Diagonal \(D = \sqrt{800}\).

    Área del círculo: \(A = \pi \left(\frac{D}{2}\right)^2 = 200\pi \approx 628 \ \text{cm}^2\).

  14. Los números \(2, 3, 5\) y \(x\) tienen un promedio igual a \(4\). ¿Cuál es \(x\)?

    Solución

    \[ \frac{2 + 3 + 5 + x}{4} = 4 \] \[ 10 + x = 16 \Rightarrow x = 6 \]
  15. Los números \(x, y, z\) y \(w\) tienen un promedio de 25. El promedio de \(x, y\) y \(z\) es 27. Encuentra \(w\).

    Solución

    \[ \frac{x + y + z + w}{4} = 25 \] \[ \frac{x + y + z}{3} = 27 \Rightarrow x + y + z = 81 \] \[ \frac{81 + w}{4} = 25 \Rightarrow w = 19 \]
  16. Encuentra \(x, y, z\) para que los números \(41, 46, x, y, z\) tengan una media aritmética de 50 y una moda de 45.

    Solución

    Media: \(\frac{41 + 46 + x + y + z}{5} = 50 \Rightarrow x + y + z = 163\).

    Moda 45 implica que 45 se repite: \(x = y = 45\). Entonces \(45 + 45 + z = 163 \Rightarrow z = 73\).

  17. \(A\) es una constante. Encuentra \(A\) tal que la ecuación \(2x + 1 = 2A + 3(x + A)\) tenga una solución en \(x = 2\).

    Solución

    Sustituimos \(x = 2\):

    \[ 2(2) + 1 = 2A + 3(2 + A) \] \[ 5 = 2A + 6 + 3A \Rightarrow A = -\frac{1}{5} \]
  18. 1 litro es igual a \(1\ \text{dm}^3\) y 1 litro de agua pesa 1 kilogramo. ¿Cuál es el peso del agua contenida en un recipiente cilíndrico con radio igual a \(50\ \text{cm}\) y altura igual a \(1\ \text{m}\)?

    Solución

    Radio: \(5\ \text{dm}\), altura: \(10\ \text{dm}\).

    Volumen: \(V = \pi \times 5^2 \times 10 = 785\ \text{dm}^3\).

    Peso: \(785\ \text{kg}\).

  19. En la figura, el triángulo \(ABC\) es un triángulo rectángulo isósceles. \(AM \perp BC\) y \(MN \perp AC\). Encuentra la razón del área del triángulo \(MNC\) al área del triángulo \(ABC\).

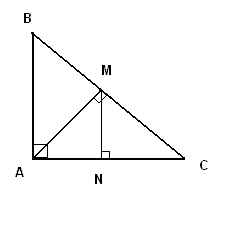
    problema 18

    Solución

    Área de \(AMC\) es la mitad del área de \(ABC\). Área de \(MNC\) es la mitad del área de \(AMC\).

    Por lo tanto, \(\frac{\text{Área de } MNC}{\text{Área de } ABC} = \frac{1}{4}\).

  20. La bomba A puede llenar un tanque de agua en 4 horas. La bomba B puede llenar el mismo tanque en 6 horas. Ambas bombas se encienden a las 8:00 a.m. para llenar el tanque vacío. Una hora después, la bomba B se descompone y tarda una hora en repararse antes de reiniciarse. ¿A qué hora se llenará el tanque? (redondea al minuto más cercano).

    Solución

    Tasa de A: \(\frac{1}{4}\) tanque/hora, tasa de B: \(\frac{1}{6}\) tanque/hora.

    Sea \(t\) el tiempo total que trabaja A. B trabaja \(t - 1\) horas.

    \[ \frac{t}{4} + \frac{t - 1}{6} = 1 \] \[ 6t + 4(t - 1) = 24 \Rightarrow t = 2.8 \ \text{horas} = 2 \ \text{horas} \ 48 \ \text{minutos} \]

    El tanque se llena a las 10:48 a.m.

  21. ¿Las rectas con ecuaciones \(2x + y = 2\) y \(x - 2y = 0\) son paralelas, perpendiculares o ninguna?

    Solución

    Pendiente de la primera: \(m_1 = -2\). Pendiente de la segunda: \(m_2 = \frac{1}{2}\).

    Producto: \(m_1 \times m_2 = -1\), por lo tanto son perpendiculares.

  22. ¿Cuáles son las dimensiones del cuadrado que tiene el perímetro y el área iguales en valor?

    Solución

    Sea \(x\) el lado del cuadrado: \(4x = x^2 \Rightarrow x^2 - 4x = 0 \Rightarrow x(x - 4) = 0\).

    Solución válida: \(x = 4\) unidades.

  23. Encuentra las dimensiones del rectángulo que tiene un largo 3 metros mayor que su ancho y un perímetro igual en valor a su área.

    Solución

    Sea \(L\) el largo y \(W\) el ancho: \(L = W + 3\).

    Perímetro = Área: \(2L + 2W = LW\).

    Sustituyendo: \(2(W + 3) + 2W = (W + 3)W \Rightarrow W^2 - W - 6 = 0\).

    Solución: \(W = 3\) metros, \(L = 6\) metros.

  24. Encuentra la circunferencia de un disco circular cuya área es \(100\pi\) cm².

    Solución

    Área: \(\pi R^2 = 100\pi \Rightarrow R = 10\) cm.

    Circunferencia: \(C = 2\pi R = 20\pi\) cm.

  25. El semicírculo de área \(50\pi\) cm² está inscrito dentro de un rectángulo. El diámetro del semicírculo coincide con el largo del rectángulo. Encuentra el área del rectángulo.

    Solución

    Área del semicírculo: \(\frac{1}{2} \pi R^2 = 50\pi \Rightarrow R = 10\) cm.

    Largo del rectángulo: \(2R = 20\) cm, ancho: \(R = 10\) cm.

    Área del rectángulo: \(20 \times 10 = 200\) cm².

  26. Un triángulo tiene un área de \(200 \ \text{cm}^2\). Dos lados de este triángulo miden 26 y 40 cm respectivamente. Encuentra el valor exacto del tercer lado.

    Solución

    Usando la fórmula del área: \(A = \frac{1}{2} a b \sin \alpha\) y la ley de los cosenos.

    El tercer lado \(c\) viene dado por:

    \[ c = \sqrt{a^2 + b^2 \pm \sqrt{4 a^2 b^2 - 16 A^2}} \]

    Sustituyendo \(a = 26\), \(b = 40\), \(A = 200\):

    \[ c_1 = \sqrt{356} = 2\sqrt{89}, \quad c_2 = \sqrt{4196} = 2\sqrt{1049} \]

Respuestas a las Preguntas Anteriores

  1. \(x = 0 , x = 1\)
  2. \(x = 0, x = 2\)
  3. \(x = 0, x = 4\)
  4. \(48 \text{ millas por hora}\)
  5. \(136 \text{ millas}\)
  6. \(12{:}05 \text{ p.m.}\)
  7. \(5y + 3x = 13\)
  8. \(\text{largo} = 30 \text{ metros}, \ \text{ancho} = 10 \text{ metros}\)
  9. \text{no hay suficiente información para resolver el problema}
  10. \(50 \text{ metros}\)
  11. \(72 \sqrt{3} \ \text{cm}^2\)
  12. \(80 \pi \ \text{cm}^3\)
  13. \(200 \pi \ \text{cm}^2\)
  14. \(x = 6\)
  15. \(w = 19\)
  16. \(x = 45, \ y = 45, \ z = 73\)
  17. \(A = -\frac{1}{5}\)
  18. \(785 \ \text{kg}\)
  19. \(1:4\)
  20. \(10{:}48 \text{ a.m.}\)
  21. perpendiculares
  22. \(\text{cuadrado con lado} = 4 \ \text{unidades}\)
  23. \(\text{largo} = 6 \ \text{unidades}, \ \text{ancho} = 3 \ \text{unidades}\)
  24. \(20 \pi \ \text{cm}\)
  25. \(200 \ \text{cm}^2\)
  26. \text{dos soluciones: } 2\sqrt{89} \text{ y } 2\sqrt{1049}

Referencias