|
|
-
Verdadero o falso: Dos líneas paralelas se cruzan.
Solución
Falso: dos líneas paralelas no se cruzan.
-
Un triángulo es una forma planar cerrada con
Solución
3 lados. ( tri en la palabra triángulo significa tres, del latín)
-
Una forma planar cerrada con 5 lados se llama
Solución
pentágono. ( penta en la palabra Pentágono significa cinco, del griego)
-
Una forma planar cerrada con 4 lados se llama
Solución
cuadrilátero. ( quadri en la palabra cuadrilátero significa cuatro, del latín)
-
Un segmento de línea se define por
Solución
2 puntos
-
Un triángulo equilátero tiene
<< br>
Solución
los tres lados iguales.
-
¿Cuál de las siguientes afirmaciones describe mejor un cuadrado?
Solución
Un cuadrado tiene 4 lados iguales y 4 ángulos rectos.
-
¿Qué par de líneas son paralelas?
 .
Solución
El par de líneas en A son paralelas porque no se cruzan.
-
¿Cuáles de estas formas son
- cuadriláteros?
- triángulos?
- cuadrados?
 .
Solución
i) los cuadriláteros tienen 4 lados: formas B, E F.
ii) los triángulos tienen 3 lados: formas A, D.
iii) los cuadrados tienen 4 lados iguales y 4 ángulos rectos: forma F.
-
¿Cuáles de estas formas son
- triángulos rectos?
- rectángulos?
 .
Solución
i) triángulos rectos tienen 1 ángulo recto: forma B.
ii) los rectángulos tienen 2 pares de lados paralelos y 4 ángulos rectos: las formas D y E.
-
Qué par de líneas son
- paralelo?
- perpendicular?
 .
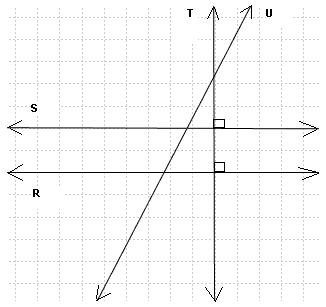
Solución
i) las líneas paralelas no se cruzan. Las líneas S y R son paralelas
ii) las líneas perpendiculares se intersectan y forman un ángulo recto (90 grados). T y S, y T y R son pares de líneas perpendiculares.
-
Encuentra el perímetro y el área de cada forma.
 .
Solución
Forma A
Perímetro = 5 + 5 + 5 + 5 = 20
Área = 5 × 5 = 25
Forma B
Perímetro = 9 + 6 + 9 + 6 = 30
Área = 9 × 6 = 54
Forma C
Perímetro = 10 + 2 + 10 + 2 = 24
Área = 10 × 2 = 20
Forma D
Perímetro = 5 + 4 + 5 + 4 = 18
Área = 5 × 4 = 20
-
Encuentra el perímetro y el área de cada forma.
 .
Solución
Forma A: el perímetro se obtiene agregando todos los lados. Comenzando por el lado superior tenemos
Perímetro = 4 + 4 + 4 + 4 + 8 + 8 = 32
Forma A: el área de la forma dada es igual al área del cuadrado del lado 8 del cual se resta el área de la pequeña parte superior cuadrada derecha del lado 4.
Área = 8 × 8 - 4 × 4 = 64 - 16 = 48
Forma B: el perímetro se obtiene agregando todos los lados. Comenzando por el lado superior tenemos
Perímetro = 8 + 2 + 4 + 4 + 4 + 2 + 8 + 8 = 40
Forma B: el área de la forma dada es igual al área del cuadrado (lado izquierdo) del lado 8 al que se agrega el área del cuadrado pequeño (lado derecho) del lado 4 .
Área = 8 × 8 + 4 × 4 = 64 + 16 = 80
-
¿Cuál de estos es un triángulo isósceles?
 .
Solución
Un triángulo isósceles tiene dos lados iguales: forma B
-
¿Qué par de triángulos son congruentes?
 .
Solución
Las formas congruentes tienen lados de igual longitud: formas A y C
-
El punto O es el centro del círculo a continuación. ¿Cómo llamas a los segmentos?
- AB?
- CD?
- ¿OD?
 .
Solución
Un segmento cuyos puntos finales están en un círculo se llama acorde: AB es un acorde
Un acorde que pasa por el centro del círculo se llama diámetro: CD es un dímetro
Un segmento cuyos 2 puntos finales son: 1) el centro del círculo y 2) un punto del círculo se llama radio: OD es un radio
Más Matemáticas primarias (grados 4 y 5) con preguntas gratuitas y problemas con respuestas
Más Matemáticas de la escuela media (grados 6, 7, 8 y 9) con preguntas gratuitas y problemas con respuestas
Más High School Math (Grados 10, 11 y 12): preguntas gratuitas y problemas con respuestas
Autor -
correo electrónico
Página de inicio
Actualizado: 8 de marzo de 2018 (A Dendane)
| |
