Problemas de Matemáticas con Soluciones para 5º Grado
Se presentan problemas de palabras y patrones para 5º grado, suma y resta de tiempo, tiempo-distancia-velocidad, fracciones y números mixtos, proporciones, porcentajes, área y volumen de rectángulos y cuadrados. Cada problema incluye soluciones detalladas y explicaciones claras. También se incluyen algunos problemas desafiantes para desarrollar el pensamiento y la confianza.
Pregunta 1
Sarah horneó un pastel y lo cortó en 8 rebanadas iguales. Ella comió 3 rebanadas y su amigo Jake comió 1 rebanada. ¿Qué fracción del pastel queda? Simplifica la fracción si es posible.
Total de rebanadas = 8
Rebanadas comidas = 3 (Sarah) + 1 (Jake) = 4
Rebanadas que quedan = 8 - 4 = 4
\[ \text{La fracción que queda} = \dfrac{4}{8} \]
Divide el numerador y el denominador entre 4:
\[ \text{La fracción que queda} = \dfrac{4\div 4}{8\div 4} = \dfrac{1}{2} \]
Queda la mitad del pastel.
Pregunta 2
Una librería vende libros a $15 cada uno. Si un cliente compra 3 libros y obtiene un descuento del 25% en el precio total, ¿cuánto pagará el cliente en total?
Precio total antes del descuento: \[ 3 \times 15 = 45 \; \text{dólares} \]
Descuento total: \[ 25\% \; \text{de} \; 45 = \dfrac{25}{100} \times 45 = 0.25 \times 45 = 11.25 \; \text{dólares} \]
Precio total después del descuento: \[ 45 - 11.25 = 33.75 \; \text{dólares} \]
El cliente pagará $33.75.
Pregunta 3
Los primeros cuatro números en una secuencia son 3, 6, 12, 24. Explica el patrón y encuentra el séptimo número en la secuencia.
El patrón comienza con 3 y luego cada número se multiplica por 2 para obtener el siguiente número.
1º: 3
2º: \( 3 \times 2 = 6 \)
3º: \( 6 \times 2 = 12 \)
4º: \( 12 \times 2 = 24 \)
5º: \( 24 \times 2 = 48 \)
6º: \( 48 \times 2 = 96 \)
7º: \( 96 \times 2 = 192 \)
El séptimo número en la secuencia es 192.
Pregunta 4
A John le toma 25 minutos caminar al estacionamiento y 45 minutos conducir al trabajo. ¿A qué hora debe salir de casa para llegar al trabajo a las 9:00 a.m.?
El tiempo total que le toma a John llegar al trabajo es la suma del tiempo para caminar al estacionamiento y el tiempo para conducir:
\[ \text{Tiempo total} = 25 + 45 = 70 \text{ minutos} \]
Dado que \( 70 \text{ minutos} = 1 \text{ hora y } 10 \text{ minutos} \), John necesita salir de casa 1 hora y 10 minutos antes de las 9:00 a.m.:
\[ 9:00 - 1:10 = 7:50 \text{ a.m.} \]
John debe salir de casa a las 7:50 a.m.
Pregunta 5
Kim puede caminar \( 4 \) kilómetros en una hora. ¿Cuánto tiempo le toma a Kim caminar \( 18 \) kilómetros?
Si Kim camina \( 4 \) km en \( 1 \) hora, entonces el tiempo para caminar \( 18 \) km es:
\[ \dfrac{18}{4} = 4.5 = 4 \frac{1}{2} \text{ horas} \]
Le toma a Kim 4.5 horas (o 4 horas y 30 minutos) caminar 18 kilómetros.
Pregunta 6
Una fábrica produjo 2,300 televisores en su primer año de producción. Se produjeron 4,500 televisores en su segundo año, y en su tercer año se produjeron 500 televisores más que en el segundo año. ¿Cuántos televisores se produjeron en tres años?
En el tercer año se produjeron 500 televisores más que en el segundo año, por lo tanto:
\[ 4500 + 500 = 5000 \text{ televisores en el tercer año} \]
El número total de televisores producidos en tres años es:
\[ 2300 + 4500 + 5000 = 11800 \]
Se produjeron 11,800 televisores en tres años.
Pregunta 7
Tom y Bob tienen un total de 49 juguetes. Si Bob tiene 5 juguetes más que Tom, ¿cuántos juguetes tiene cada uno?
Si se quitan 5 juguetes de los 49 y el resto se distribuye equitativamente, ambos tendrán la misma cantidad de juguetes.
\[ 49 - 5 = 44 \text{ (para compartir equitativamente)} \]
Si se distribuyen equitativamente, cada uno tendrá:
\[ \dfrac{44}{2} = 22 \text{ juguetes} \]
Bob tiene 5 juguetes más que Tom, entonces Bob tiene:
\[ 22 + 5 = 27 \text{ juguetes} \]
Tom tiene 22 juguetes y Bob tiene 27 juguetes.
Nota: verifica que el total sea 49 y que Bob tenga 5 juguetes más que Tom.
Pregunta 8
John puede comer un cuarto de pizza en un minuto. ¿Cuánto tiempo le toma a John comer una pizza y media?
Método 1: Hay 4 cuartos en una pizza entera y 2 cuartos en media pizza. Entonces, en total, una pizza y media tiene:
\[ 4 + 2 = 6 \text{ cuartos} \]
Si John come un cuarto en un minuto, necesita:
\[ 6 \times 1 = 6 \text{ minutos} \]
para comer una pizza y media.
Método 2: Usando fracciones:
Una pizza y media se escribe como: \( 1\frac{1}{2} \)
Convertimos a fracción impropia: \( 1\frac{1}{2} = \frac{3}{2} \)
Dividimos entre \( \frac{1}{4} \) para encontrar cuántos cuartos hay:
\[ \frac{3}{2} \div \frac{1}{4} = \frac{3}{2} \times \frac{4}{1} = \frac{12}{2} = 6 \]
Hay 6 cuartos, por lo tanto John necesita 6 minutos.
Pregunta 9
John leyó un cuarto del tiempo que leyó Tom. Tom leyó solo dos quintos del tiempo que leyó Sasha. Sasha leyó el doble de tiempo que Mike. Si Mike leyó 5 horas, ¿cuánto tiempo leyó John?
Mike leyó 5 horas. Sasha leyó el doble que Mike:
\[ 2 \times 5 = 10 \text{ horas} \]
Tom leyó dos quintos del tiempo que leyó Sasha:
\[ \frac{2}{5} \times 10 = 4 \text{ horas} \]
John leyó un cuarto del tiempo que leyó Tom:
\[ \frac{1}{4} \times 4 = 1 \text{ hora} \]
John leyó durante 1 hora.
Pregunta 11
Jim, Carla y Tomy son miembros de la misma familia. Carla es 5 años mayor que Jim. Tomy es 6 años mayor que Carla. La suma de sus tres edades es 31 años. ¿Qué edad tiene cada uno?
Método algebraico:
Sea \( x \) la edad de Jim.
Carla es 5 años mayor que Jim: \( x + 5 \)
Tomy es 6 años mayor que Carla: \( x + 5 + 6 = x + 11 \)
La suma de las edades es 31:
\[ x + (x + 5) + (x + 11) = 31 \]
\[ 3x + 16 = 31 \]
\[ 3x = 15 \]
\[ x = 5 \]
Jim tiene 5 años, Carla tiene 10 años y Tomy tiene 16 años.
Método de tabla:
| Edad de Jim | Edad de Carla | Edad de Tomy | Suma de edades |
|---|---|---|---|
| 1 | 6 | 12 | 19 |
| 2 | 7 | 13 | 22 |
| 3 | 8 | 14 | 25 |
| 4 | 9 | 15 | 28 |
| 5 | 10 | 16 | 31 |
Jim tiene 5 años, Carla 10 años y Tomy 16 años.
Pregunta 12
Mel tenía $35.00 y retiró más dinero de su cuenta bancaria. Compró un par de pantalones por $34.00, dos camisas a $16.00 cada una y dos pares de zapatos a $24.00 cada uno. Después de comprar, le quedaron $32.00. ¿Cuánto dinero retiró Mel del banco?
Gastos de Mel:
Pantalones: $34.00
Dos camisas: \( 2 \times 16.00 = $32.00 \)
Dos pares de zapatos: \( 2 \times 24.00 = $48.00 \)
Gasto total: \( 34.00 + 32.00 + 48.00 = $114.00 \)
Le quedaron $32.00, entonces tenía antes de comprar:
\[ 114.00 + 32.00 = $146.00 \]
Este total incluye los $35.00 originales más lo que retiró:
\[ 146.00 - 35.00 = $111.00 \]
Mel retiró $111.00 del banco.
Pregunta 13
¿Cuántos minutos hay en una semana?
1 semana = 7 días
1 día = 24 horas
1 hora = 60 minutos
Entonces, en una semana hay:
\[ 7 \times 24 \times 60 = 10080 \text{ minutos} \]
Pregunta 14
En la casa de Tim, una piscina rectangular (azul) de 30 metros de largo y 10 metros de ancho está rodeada de césped (verde). La piscina con el área de césped forman un rectángulo grande de 50 metros de largo y 20 metros de ancho. ¿Qué área ocupa el césped?
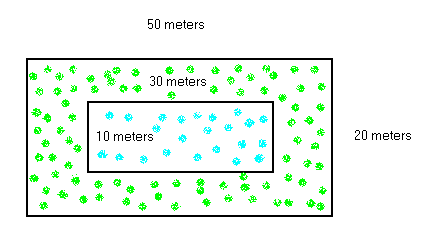
Área del rectángulo grande (piscina + césped):
\[ 50 \times 20 = 1000 \text{ m}^2 \]
Área de la piscina:
\[ 30 \times 10 = 300 \text{ m}^2 \]
Área del césped:
\[ 1000 - 300 = 700 \text{ m}^2 \]
Pregunta 15
María quiere hacer una caja. Comienza con un cartón de 15 cm de largo y 10 cm de ancho. Luego corta cuadrados congruentes de 3 cm de lado en cada una de las cuatro esquinas. ¿Cuál es el área del cartón después de cortar las 4 esquinas?
Área total del cartón antes de cortar:
\[ 15 \times 10 = 150 \text{ cm}^2 \]
Área de un cuadrado cortado:
\[ 3 \times 3 = 9 \text{ cm}^2 \]
Área total cortada (4 cuadrados):
\[ 4 \times 9 = 36 \text{ cm}^2 \]
Área del cartón después de cortar:
\[ 150 - 36 = 114 \text{ cm}^2 \]
Pregunta 16
Un pintor cobra $225.00 por materiales y $35.00 por hora de mano de obra. El costo total para pintar una oficina es $330.00. ¿Cuántas horas le tomó al pintor pintar la oficina?
Costo de mano de obra:
\[ 330.00 - 225.00 = $105.00 \]
Si cobra $35.00 por hora:
\[ \frac{105.00}{35} = 3 \text{ horas} \]
Le tomó 3 horas pintar la oficina.
Pregunta 17
Tres carros de juguete y 4 trenes de juguete cuestan $18. Dos carros de juguete y 3 trenes de juguete cuestan $13. ¿Cuál es el precio de un carro de juguete y el precio de un tren de juguete si ambos precios son números enteros de dólares?
Usando una tabla:
| Precio carro | Precio tren | 3 carros + 4 trenes | 2 carros + 3 trenes |
|---|---|---|---|
| $2 | $3 | $18 | $13 |
Un carro de juguete cuesta $2 y un tren de juguete cuesta $3.
Pregunta 18
Una caja tiene una longitud de 5 cm, un ancho de 3 cm y una altura de 4 cm. ¿Cuál es el volumen de la caja?
Volumen = largo × ancho × alto
\[ 5 \times 3 \times 4 = 60 \text{ cm}^3 \]
El volumen de la caja es 60 cm³.
Pregunta 19
Una bolsa contiene 6 bolas rojas, 4 bolas azules y 10 bolas verdes. Si se elige una bola al azar, ¿cuál es la probabilidad de que la bola sea azul? Escribe tu respuesta como fracción simplificada.
Total de bolas:
\[ 6 + 4 + 10 = 20 \]
Bolas azules: 4
Probabilidad de elegir una bola azul:
\[ \frac{4}{20} = \frac{1}{5} \]
Pregunta 20
John compró 3.75 metros de tela para hacer una cortina. Usó 2.4 metros para una cortina y 0.85 metros para otra. ¿Cuánta tela le queda?
Tela usada:
\[ 2.4 + 0.85 = 3.25 \text{ metros} \]
Tela que queda:
\[ 3.75 - 3.25 = 0.5 \text{ metros} \]
Le quedan 0.5 metros de tela.
Pregunta 21
Linda gastó \( \frac{3}{4} \) de sus ahorros en muebles. Luego gastó \( \frac{1}{2} \) de sus ahorros restantes en un refrigerador. Si el refrigerador le costó $150, ¿cuáles eran sus ahorros originales?
Sea \( x \) los ahorros originales.
Después de comprar muebles le queda: \( \frac{1}{4}x \)
Gasta \( \frac{1}{2} \) de esto en el refrigerador: \( \frac{1}{2} \times \frac{1}{4}x = \frac{1}{8}x \)
Este gasto es $150: \( \frac{1}{8}x = 150 \)
\[ x = 150 \times 8 = 1200 \]
Sus ahorros originales eran $1200.
Pregunta 22
El perímetro del cuadrado A es 3 veces el perímetro del cuadrado B. ¿Cuál es la razón del área del cuadrado A al área del cuadrado B?
Sea \( x \) el lado del cuadrado A y \( y \) el lado del cuadrado B.
Perímetro A: \( 4x \)
Perímetro B: \( 4y \)
Dado: \( 4x = 3(4y) = 12y \)
\[ x = 3y \]
Área A: \( x^2 \)
Área B: \( y^2 \)
Razón de áreas: \( \frac{x^2}{y^2} = \frac{(3y)^2}{y^2} = \frac{9y^2}{y^2} = 9 \)
La razón del área de A a B es 9:1.
Pregunta 23
María quiere hacer una caja rectangular abierta. Comienza con un cartón de 15 cm de largo y 10 cm de ancho. Luego corta 4 cuadrados congruentes de 3 cm de lado en las cuatro esquinas y dobla por las líneas para hacer la caja. ¿Cuál es el volumen de la caja?
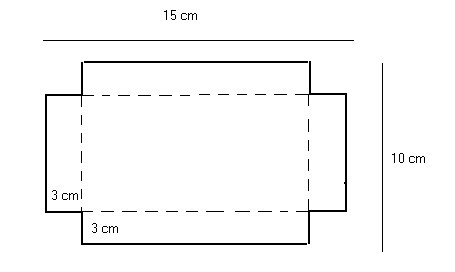
Largo de la caja: \( 15 - 3 - 3 = 9 \text{ cm} \)
Ancho de la caja: \( 10 - 3 - 3 = 4 \text{ cm} \)
Alto de la caja: \( 3 \text{ cm} \)
Volumen: \( 9 \times 4 \times 3 = 108 \text{ cm}^3 \)
Pregunta 24
Se corta un pequeño cuadrado de lado \( 2x \) de una esquina de un rectángulo cuyo ancho es 10 cm y largo 20 cm. Escribe una expresión en términos de \( x \) para el área de la figura restante.
Área del rectángulo: \( 20 \times 10 = 200 \)
Área del cuadrado: \( (2x) \times (2x) = 4x^2 \)
Área restante: \( 200 - 4x^2 \)
Pregunta 25
Las coordenadas del punto A son (2, 3) y las coordenadas del punto B son (6, 7). ¿Cuál es la distancia \( d \) entre los puntos A y B? (Usa la fórmula de distancia: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \))
Usando la fórmula de distancia:
\[ d = \sqrt{(6 - 2)^2 + (7 - 3)^2} \]
\[ d = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2} \]
La distancia es \( 4\sqrt{2} \) unidades (aproximadamente 5.66 unidades).