Soluciones a los Problemas
-
Una caja grande contiene 18 cajas pequeñas y cada caja pequeña contiene 25 barras de chocolate. ¿Cuántas barras de chocolate hay en la caja grande?
SoluciónEl número de barras de chocolate es igual a:
18 × 25 = 450 -
A John le toma 25 minutos caminar al estacionamiento y 45 minutos manejar al trabajo. ¿A qué hora debe salir de casa para llegar al trabajo a las 9:00 a.m.?
SoluciónEl tiempo que le toma a John llegar al trabajo: tiempo caminando + tiempo manejando.
Tiempo = 25 + 45 = 70 minutos = 60 minutos + 10 minutos.
Sabemos que 1 hora = 60 minutos, entonces:
Tiempo = 1 hora + 10 minutos.
John necesita salir de casa 1 hora y 10 minutos antes de las 9:00 a.m., es decir, a las:
9:00 - 1:10 = 7:50 a.m. -
Kim puede caminar 4 kilómetros en una hora. ¿Cuánto tiempo le toma a Kim caminar 18 kilómetros?
SoluciónEl tiempo que le toma a Kim caminar 18 kilómetros es igual a:
Tiempo = Distancia / Velocidad
Tiempo = 18 / 4 = 4,5 horas = (4 + 0,5) horas = 4 y 1/2 horas.
Sabemos que 1/2 hora = 30 minutos, por lo tanto:
Tiempo = 4 horas y 30 minutos. -
Una fábrica produjo 2300 televisores en su primer año de producción. 4500 sets fueron producidos en su segundo año y se produjeron 500 televisores más en su tercer año que en el segundo año. ¿Cuántos televisores se produjeron en tres años?
SoluciónSe produjeron 500 televisores más en el tercer año que en el segundo. El número de sets producidos en el tercer año es igual a:
4500 + 500 = 5000.
El número total de televisores producidos en tres años es igual a la suma de los producidos cada año:
2300 + 4500 + 5000 = 11800. -
Linda compró 3 cuadernos a $1.20 cada uno; una caja de lápices a $1,50 y una caja de bolígrafos a $1,70. ¿Cuánto gastó Linda?
SoluciónLinda gastó en cuadernos:
1,20 × 3 = $3,60.
La cantidad total de dinero que Linda gastó es:
3,60 + 1,50 + 1,70 = $6,80. -
Tom y Bob tienen un total de 49 juguetes. Si Bob tiene 5 juguetes más que Tom, ¿cuántos juguetes tiene cada uno?
SoluciónSi se quitan 5 juguetes de los 49 y se distribuyen los restantes entre Tom y Bob, ambos tendrán la misma cantidad.
49 - 5 = 44 juguetes para repartir.
Si se distribuyen equitativamente, cada uno tendrá:
44 ÷ 2 = 22 juguetes.
Bob tiene 5 más que Tom, así que Bob tiene:
22 + 5 = 27 juguetes.
Bob tiene 27 y Tom tiene 22. Es fácil verificar que entre ambos tienen 49 y la diferencia es 5. -
John puede comer un cuarto de pizza en un minuto. ¿Cuánto tiempo le toma a John comerse una pizza y media?
SoluciónDos soluciones posibles:
1) Hay 4 cuartos en una pizza y 2 cuartos en media pizza. Así que hay un total de 6 cuartos en una pizza y media. Si John come un cuarto por minuto, necesita 6 minutos para comer los 6 cuartos.
2) Una pizza y media se escribe como número mixto: 1(1/2). John necesita un minuto para comer un cuarto. El número de cuartos en una pizza y media se encuentra con la división:
(1 (1/2)) ÷ 1/4.
Convertimos el número mixto a fracción impropia:
1 (1/2) = 2/2 + 1/2 = 3/2.
El número de cuartos es:
(3/2) ÷ 1/4 = (3/2) × (4/1) = 12 / 2 = 6 cuartos.
John necesita 6 minutos. -
John puede comer un sexto de pizza en dos minutos. A Billy le toma 3 minutos comer un cuarto de la misma pizza. Si John y Billy comienzan a comer una pizza cada uno, ¿quién terminará primero?
SoluciónEn una pizza hay 6 sextos, así que John tardará:
2 × 6 = 12 minutos en terminar una pizza.
En una pizza hay 4 cuartos, así que Billy tardará:
3 × 4 = 12 minutos en terminar una pizza.
A cada uno le toma 12 minutos, por lo que terminarán al mismo tiempo. -
John leyó la cuarta parte del tiempo que Tom leyó. Tom leyó solo dos quintos del tiempo que Sasha leyó. Sasha leyó el doble de tiempo que Mike. Si Mike leyó 5 horas, ¿cuánto tiempo leyó John?
SoluciónMike leyó 5 horas. Sasha leyó el doble:
2 × 5 = 10 horas.
Tom leyó dos quintos del tiempo de Sasha:
(2 / 5) × 10 = 4 horas.
John leyó un cuarto del tiempo de Tom:
(1 / 4) × 4 = 1 hora. -
Jim, Carla y Tomy son miembros de la misma familia. Carla es 5 años mayor que Jim. Tomy es 6 años mayor que Carla. La suma de sus tres edades es 31 años. ¿Cuántos años tiene cada uno?
SoluciónEste problema se puede resolver con una tabla donde se supone la edad de Jim y se calculan las edades de Carla y Tomy. Los cálculos se detienen cuando se cumple la condición: "la suma de sus tres edades es 31 años".
Edad de Jim Edad de Carla Edad de Tomy Suma de las edades 1 1 + 5 = 6 6 + 6 = 12 1 + 6 + 12 = 19 2 2 + 5 =7 7 + 6 = 13 2+ 7 + 13 = 22 3 3 + 5 = 8 8 + 6 = 14 3 + 8 + 14 = 25 4 4 + 5 = 9 9 + 6 = 15 4 + 9 + 15 = 28 5 5 + 5 = 10 10 + 6 = 16 5 + 10 + 16 = 31
La última fila muestra que Jim (5), Carla (10) y Tomy (16) satisfacen la condición. -
Mel tenía $35,00 y retiró más dinero de su cuenta bancaria. Compró un par de pantalones por $34,00, dos camisas por $16,00 cada una y 2 pares de zapatos por $24,00 cada uno. Después de comprar, le quedaban $32.00. ¿Cuánto dinero retiró Mel del banco?
SoluciónMel gastó:
$34,00 en pantalones.
2 × 16,00 = $32,00 en camisas.
2 × 24,00 = $48,00 en zapatos.
El total gastado es:
$34,00 + $32,00 + $48,00 = $114,00.
Le quedaban $32,00, así que el dinero total que tenía antes de comprar es:
$114,00 + $32,00 = $146,00.
Este total incluye los $35,00 iniciales y lo que retiró. Por lo tanto, retiró:
$146,00 - $35,00 = $111,00. -
¿Cuántos minutos hay en una semana?
Solución1 semana = 7 días.
1 día = 24 horas.
1 hora = 60 minutos.
Por lo tanto, en una semana hay:
7 × 24 × 60 = 10080 minutos. -
En la casa de Tim, una piscina rectangular (azul) de 30 metros de largo y 10 metros de ancho está rodeada de césped (verde). La piscina con el área de césped forman un rectángulo grande de 50 metros de largo y 20 metros de ancho. ¿Qué área ocupa el césped?
Solución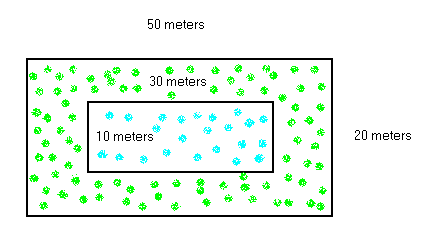
El área de un rectángulo es: Área = Largo × ancho.
Área del rectángulo grande (piscina y césped) = 50 × 20 = 1000 metros cuadrados.
Área de la piscina = 30 × 10 = 300 metros cuadrados.
Área del césped = Área grande - Área piscina = 1000 - 300 = 700 metros cuadrados. -
Mary quiere hacer una caja. Comienza con un cartón de 15 centímetros de largo y 10 de ancho. Luego corta cuadrados congruentes de 3 centímetros de lado en las cuatro esquinas. ¿Cuál es el área del cartón después de cortar las 4 esquinas?
Solución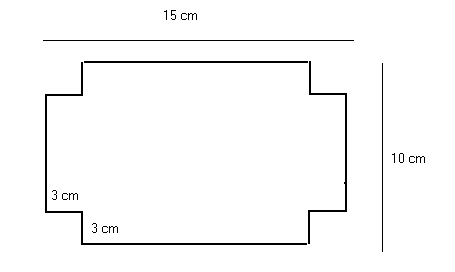
El área total del cartón antes de cortar es:
Área = 15 × 10 = 150 centímetros cuadrados.
Área de 1 cuadrado en una esquina = 3 × 3 = 9 cm².
Se cortan 4 cuadrados, por lo que el área total recortada es:
4 × 9 = 36 cm².
El área del cartón después del corte es:
150 - 36 = 114 cm². -
Un pintor cobra $225,00 por materiales y $35,00 por hora de mano de obra. El costo total de pintar una oficina es $330,00. ¿Cuántas horas le tomó al pintor pintar la oficina?
SoluciónRestando el costo de materiales del total, obtenemos el costo de la mano de obra:
$330,00 - $225,00 = $105,00.
Este $105,00 es el costo por trabajo a $35,00 por hora, por lo tanto el número de horas es:
105,00 ÷ 35 = 3 horas. -
Tres carros de juguete y 4 trenes de juguete cuestan $18. Dos carros de juguete y 3 trenes de juguete cuestan $13. ¿Cuál es el precio de un carro y el precio de un tren si ambos precios son números enteros de Dólares? (Pista: Usa una tabla)
SoluciónUsa una tabla y supón el precio de un carro y un tren, luego calcula y verifica las dos condiciones.
1) Condición 1: Tres carros y 4 trenes deben costar $18.
2) Condición 2: Dos carros y 3 trenes deben costar $13.
La tabla muestra que ambas condiciones se cumplen cuando un carro cuesta $2 y un tren cuesta $3.
Supuesto precio de 1 carro Supuesto precio de 1 tren Calcula: 3 carros + 4 trenes Calcula: 2 carros + 3 trenes 1 1 3×1+4×1 = 7 No necesario 1 2 3×1+4×2 = 11 No necesario 1 3 3×1+4×3 = 15 No necesario 1 4 3×1+4×4 = 19 No necesario 2 1 3×2+4×1 = 10 No necesario 2 2 3×2+4×2 = 14 No necesario 2 3 3×2+4×3 = 18 2×2+3×3 = 13