Funciones en Matemáticas

Esta guía presenta la definición de función en matemáticas con ejemplos, ejercicios y sus soluciones detalladas.

Definición de Función en Matemáticas

Una función de un conjunto \( D \) a un conjunto \( R \) es una relación que asigna a cada elemento \( x \) en \( D \) exactamente un elemento \( y \) de \( R \). El conjunto \( D \) es el dominio (entradas) y el conjunto \( R \) es el rango (salidas).

Funciones representadas con diagramas de Venn

Las Figuras 1 y 2 muestran diagramas de Venn que representan funciones de \( D \) a \( R \), ya que cada entrada en \( D \) corresponde a una única salida en \( R \).

Función representada con diagrama de Venn
Fig.1 - Función (Cada entrada tiene exactamente una salida)
Función con diferentes entradas dando la misma salida
Fig.2 - Función (Diferentes entradas pueden tener la misma salida)

Nota: Que dos entradas diferentes (como 3 y 5) tengan la misma salida (0) no contradice la definición, ya que cada entrada tiene exactamente una salida.

El diagrama de Venn en la Figura 3 NO es una función porque a la entrada 6 en el dominio \( D \) le corresponden dos salidas (0 y -2).

Relación que no es función
Fig.3 - No es una función (Una entrada tiene múltiples salidas)

Funciones representadas con pares ordenados

Ejercicio

¿Cuál de las siguientes relaciones representa una función?

  1. \( R_1 = \{ (a,2), (b,4), (c,7), (d,-2) \} \)
  2. \( R_2 = \{ (a,4), (a,5), (b,5), (c,5) \} \)
  3. \( R_3 = \{ (0,4), (2,4), (4,5), (6,5) \} \)

Solución

  1. Todos los elementos del dominio de \( R_1 \) son diferentes → ES una función.
  2. A la entrada \( a \) le corresponden dos salidas diferentes (4 y 5) → NO es una función.
  3. Todos los elementos del dominio de \( R_3 \) son diferentes → ES una función.

Funciones representadas con gráficos

Ejercicio

Explica por qué las relaciones en las Figuras 4 y 6 no son funciones, mientras que la relación en la Figura 5 sí lo es.

  1. La gráfica en la Figura 4 NO es una función porque a la entrada \( x = 2 \) le corresponden dos salidas diferentes (\( y = 4 \) y \( y = 6 \)).

    Gráfica que no representa una función
    Fig.4 - No es una función (Falla la prueba de la línea vertical)

  2. La gráfica en la Figura 5 ES una función porque a cada entrada \( x \) le corresponde exactamente una salida \( y \).

    Gráfica de una función
    Fig.5 - Es una función (Cada x tiene una única y)

  3. La gráfica en la Figura 6 NO es una función porque:

    Gráfica que no representa una función
    Fig.6 - No es una función (Múltiples puntos con misma x)

Funciones representadas con ecuaciones

Las funciones pueden representarse mediante ecuaciones matemáticas como:

a) \( y = 2x - 1 \),   b) \( y = x^2 + 1 \),   c) \( y = \dfrac{1}{x} \)

Todas estas ecuaciones representan \( y \) como función de \( x \) porque para cada valor de \( x \) en el dominio, obtenemos exactamente un valor de \( y \).

\( x \) se llama variable independiente y \( y \) es la variable dependiente.

Más información sobre funciones representadas por ecuaciones.

Dominio y Rango de una Función

El dominio \( D \)) de una función es el conjunto de todos los valores de entrada para los cuales la salida está definida.

El rango \( R \)) de una función es el conjunto de todos los valores de salida correspondientes a las entradas del dominio \( D \).

Ejemplo

Encuentra el dominio y rango de funciones representadas en diferentes formas:

  1. Conjunto de pares ordenados: \( F_1 = \{ (a,2), (b,4), (c,7), (d,-2) \} \)

    Solución: \( D = \{ a, b, c, d \} \), \( R = \{ 2, 4, 7, -2 \} \)

  2. Diagrama de Venn:

    Función en diagrama de Venn
    Fig.7 - Función representada con diagrama de Venn

    Solución: \( D = \{ 0, 5, 3, -3 \} \), \( R = \{ 2, 0, 6 \} \)

  3. Gráfica:

    Gráfica de una función
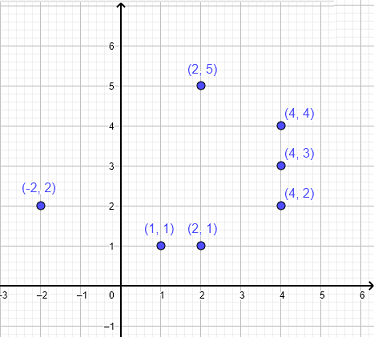
    Fig.8 - Función representada con gráfica

    Solución: \( D = \{ 2, 4, 6, 7 \} \), \( R = \{ 3, 1, 4, 2 \} \)

  4. Ecuación: \( y = -x + 3 \) para \( x \) en \( D = \{-3, 0, 6, 7\} \)

    Solución:

    \( R = \{ 6, 3, -3, -4 \} \)

Ejercicios

Parte A: Diagramas de Venn

¿Cuáles de las siguientes relaciones representadas con diagramas de Venn son funciones? Explica por qué.

Diagramas de Venn de relaciones
Fig.9 - Relaciones representadas con diagramas de Venn

Parte B: Gráficas

¿Cuáles de las siguientes relaciones representadas con gráficas son funciones? Explica por qué.

Gráficas de relaciones
Fig.10 - Relaciones representadas con gráficas

Parte C: Pares Ordenados

¿Cuáles de las siguientes relaciones representadas con pares ordenados son funciones? Explica por qué.

  1. \( R_1 = \{ (-2,2), (0,4), (9,7), (12,-2) \} \)
  2. \( R_2 = \{ (a,0), (a,7), (a,9), (a,5) \} \)
  3. \( R_3 = \{ (0,4), (2,4), (5,4), (9,4) \} \)
  4. \( R_4 = \{ (a,b), (b,a), (c,e), (d,a) \} \) (suponiendo que todas las letras tienen valores diferentes)

Parte D: Representación de Funciones

La ecuación \( y = x - 2 \) representa \( y \) como función de \( x \). Representa esta función como:

  1. Una tabla
  2. Un conjunto de pares ordenados
  3. Una gráfica
  4. Un diagrama de Venn

para los valores de \( x \) en el dominio: \( D = \{-1, 0, 1, 2\} \).

Parte E: Dominio y Rango

Encuentra el dominio y rango de las funciones representadas por:

  1. Diagrama de Venn:

    Función en diagrama de Venn
    Fig.11 - Función representada con diagrama de Venn

  2. Ecuación: \( y = \dfrac{1}{x+2} \) para \( x \) en \( D = \{0, 1, 4\} \)

  3. Gráfica:

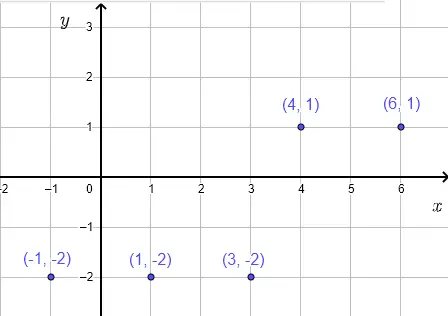
    Gráfica de función
    Fig.12 - Función representada con gráfica

Soluciones

Parte A

  1. Es una función - Cada entrada tiene exactamente una salida.
  2. NO es una función - La entrada 3 tiene dos salidas (A y B).
  3. Es una función - Cada entrada tiene exactamente una salida.
  4. NO es una función - La entrada 5 tiene tres salidas (a, b y c).

Parte B

  1. Es una función - Cada \( x \) tiene una única \( y \).
  2. NO es una función - A \( x = 1 \) le corresponden \( y = 2 \) y \( y = -2 \).
  3. NO es una función - A \( x = 1 \) le corresponden \( y = -3, -1, 1, 3 \).
  4. Es una función - Cada \( x \) tiene una única \( y \).

Parte C

  1. Es una función - Todas las entradas (primeros elementos) son diferentes.
  2. NO es una función - La entrada \( a \) tiene múltiples salidas.
  3. Es una función - Todas las entradas son diferentes.
  4. Es una función - Todas las entradas son diferentes.

Parte D

Función: \( y = x - 2 \), Dominio: \( D = \{-1, 0, 1, 2\} \)

  1. Tabla:

    \( x \)-1012
    \( y \)-3-2-10

  2. Pares ordenados: \( \{ (-1,-3), (0,-2), (1,-1), (2,0) \} \)

  3. Gráfica:

    Gráfica de la función y = x - 2
    Fig.13 - Gráfica de \( y = x - 2 \)

  4. Diagrama de Venn:

    Diagrama de Venn de la función
    Fig.14 - Función representada con diagrama de Venn

Parte E

  1. \( D = \{1, 3, 8, 12, 23\} \), \( R = \{-4, 4\} \)
  2. \( D = \{0, 1, 4\} \), \( R = \{\frac{1}{2}, \frac{1}{3}, \frac{1}{6}\} \)
  3. \( D = \{-1, 1, 3, 4, 6\} \), \( R = \{-2, 1\} \)

Referencias y Recursos Adicionales