Eventos Mutuamente Excluyentes en Probabilidad

Esta lección explica cómo determinar si dos eventos son mutuamente excluyentes. Un repaso rápido del espacio muestral y los eventos en probabilidad puede ser útil antes de continuar.

Definición: Eventos Mutuamente Excluyentes

Dos eventos se denominan mutuamente excluyentes si no pueden ocurrir al mismo tiempo.

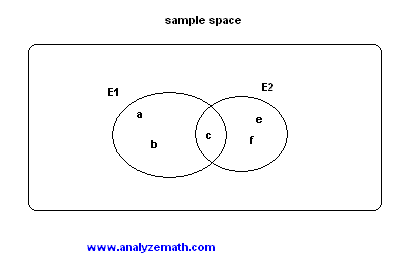
Usando notación de conjuntos, dos eventos mutuamente excluyentes \(E_1\) y \(E_2\) cumplen:

Esto significa que los dos eventos no tienen resultados en común.

Por el contrario, los eventos que no son mutuamente excluyentes comparten al menos un resultado común:

Ejemplos con Soluciones

Ejemplo 1

Se lanza un dado justo. Sea \(E_1\) el evento de que el número sea par, y \(E_2\) el evento de que el número sea impar. ¿Son \(E_1\) y \(E_2\) mutuamente excluyentes?

Solución

Dado que \(E_1 \cap E_2 = \varnothing\), los dos eventos no tienen resultados en común. Por lo tanto, \(E_1\) y \(E_2\) son mutuamente excluyentes.

El resultado de un dado no puede ser par e impar al mismo tiempo.

Ejemplo 2

Se lanza un dado. Sea \(E_1\) el evento de que el número sea par, y \(E_2\) el evento de que el número sea mayor que 3. ¿Son los eventos mutuamente excluyentes?

Solución

La intersección es:

Dado que la intersección no es vacía, los eventos no son mutuamente excluyentes.

Ejemplo 3

Se extrae una carta de una baraja estándar. Define los eventos:

• \(E_1\): sacar un 8
• \(E_2\): sacar un rey
• \(E_3\): sacar una carta con figura (sota, reina o rey)
• \(E_4\): sacar un as
• \(E_5\): sacar un corazón

Determina si los siguientes pares de eventos son mutuamente excluyentes.

• \(E_1\) y \(E_2\): mutuamente excluyentes
• \(E_2\) y \(E_3\): no mutuamente excluyentes (un rey es una carta con figura)
• \(E_3\) y \(E_4\): mutuamente excluyentes
• \(E_4\) y \(E_5\): no mutuamente excluyentes (as de corazones)
• \(E_5\) y \(E_1\): no mutuamente excluyentes (8 de corazones)

Ejemplo 4

Se lanzan dos dados. Define los eventos:

• \(E_1\): la suma es igual a 10
• \(E_2\): obtener un par (mismo número en ambos dados)
• \(E_3\): suma menor que 4
• \(E_4\): suma menor que 7

• \(E_1\) y \(E_2\): no mutuamente excluyentes \((5,5)\)
• \(E_2\) y \(E_3\): no mutuamente excluyentes \((1,1)\)
• \(E_3\) y \(E_4\): no mutuamente excluyentes
• \(E_4\) y \(E_1\): mutuamente excluyentes

Lecturas Adicionales

Estadística Elemental y Probabilidad
Página de Inicio de AnalyzeMath