Permutations and combinations are used to solve problems.
Factorial
Example 1: How many 3-digit numbers can you make using the digits 1, 2 and 3 without repetitions?
method (1) listing all possible numbers using a tree diagram.
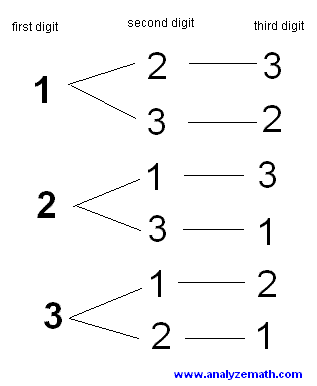
We can make 6 numbers using 3 digits and without repetitions of the digits.
method (2) counting:
LOOK AT THE TREE DIAGRAM ABOVE.
We have 3 choices for the first digit, 2 choices for the second digit and 1 choice for the third digit.
Using the counting principle, we can say:
The total number of 3-digit numbers is given by
3 × 2 × 1 = 6
There is a special notation for the product 3 × 2 × 1 = 3! and it is read 3 factorial.
In general n! is read n factorial and is given by
\[ n! = n \times (n - 1) \times (n - 2) \times ... \times 2 \times 1 \]
We also define 0! = 1.
Example 2: How many different words can we make using the letters A, B, E and L without repeating the letters?
Solution: We have 4 choices for the first letter, 3 choices for the second letter, 2 choices for the third letter and 1 choice for the fourth letter. Hence the number of words is given by
4 × 3 × 2 × 1 = 4! = 24
Permutations
Example 3: How many 2-digit numbers can you make using the digits 1, 2, 3 and 4 without repeating the digits?
This time we want to use 2 digits at the time to make 2-digit numbers.
For the first digit, we have 4 choices and for the second digit, we have 3 choices (4 - 1 used already). Using the counting principle, the number of 2 digit numbers that we can make using 4 digits is given by
4 × 3 = 12
The above problem is that of arranging 2 digits out of 4 in a specific order. This is also called permutating.
The most important idea in permutations is that order is important. When you use the digits 3 and 4 to make a number, the numbers 34 and 43 are different hence the order of the digits 3 and 4 is important.
In general permutating r (2 digit in the above example) items out of a set of n (4 digits in the above example) items is written as n P r and the formula is given by
\[ _{n}P_{r} = \dfrac{n!}{(n - r)!} \]
Example 4: Calculate
\( _{4}P_{2} \)
\( _{6}P_{5} \)
\( _{4}P_{4} \)
Solution:
Example 5: How many 3-letter words can we make with the letters in the word LOVE?
Solution: There are 4 letters in the word love and making 3-letter words is similar to arranging these 3 letters and order is important since LOV and VOL are different words because of the order of the same letters L, O and V. Hence it is a permutation problem. The number of words is given by
\( _{4}P_{3} = \dfrac{4!}{(4 - 3)!} = \dfrac{4!}{1!} = 24 \)
Combinations
Example 6: How many lines can you draw using 3 noncollinear (not in a single line) points A, B and C on a plane?
Solution:
You need two points to draw a line. The order is not important. Line AB is the same as line BA. The problem is to select 2 points out of 3 to draw different lines. If we proceed as we did with permutations, we get the following pairs of points to draw lines.
AB , AC
BA , BC
CA , CB
There is a problem: line AB is the same as line BA, same for lines AC and CA and BC and CB.
The lines are: AB, BC and AC ; 3 lines only.
So in fact we can draw 3 lines and not 6 and that's because in this problem the order of the points A, B and C is not important.
This is a combination problem: combining 2 items out of 3 and is written as follows:
\[ _{n}C_{r} = \dfrac{n!}{(n - r)! \; r!} \]
The number of combinations is equal to the number of permutations divided by r! to eliminate those counted more than once because the order is not important.
Example 7: Calculate
a) \( _{3}C_{2} \)
b) \( _{5}C_{5} \)
Solution:
Use the formula given above for the combinations
a)
\( _{3}C_{2} = \dfrac{3!}{ (3 - 2)!2! } = \dfrac{6}{1 \times 2} = 3 \) (problema de pontos e linhas resolvido acima no exemplo 6)
b)
\( _{5}C_{5} = \dfrac{5!}{(5 - 5)! \; 5!} = \dfrac{5!}{0! \; 5!} = \dfrac{ 5! }{1 * 5!} = 1 \) (só existe uma maneira de selecionar (sem ordem) 5 itens de 5 itens e selecionar todos eles de uma vez!)
Example 8:We need to form a 5-a-side team in a class of 12 students. How many different teams can be formed?
Solution:
There is nothing that indicates that the order in which the team members are selected is important and therefore it is a combination problem. Hence the number of teams is given by
\( _{12}C_{5} = \dfrac{12!}{(12 - 5)! \; 5!} = 792 \)
Problems with solutions
How many 4-digit numbers can we make using the digits 3, 6, 7 and 8 without repetitions?
How many 3-digit numbers can we make using the digits 2, 3, 4, 5, and 6 without repetitions?
How many 6-letter words can we make using the letters in the word LIBERTY without repetitions?
In how many ways can you arrange 5 different books on a shelf?
In how many ways can you select a committee of 3 students out of 10 students?
How many triangles can you make using 6 noncollinear points on a plane?
A committee including 3 boys and 4 girls is to be formed from a group of 10 boys and 12 girls. How many different committees can be formed from the group?
In a certain country, the car number plate is formed by 4 digits from the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 followed by 3 letters from the alphabet. How many number plates can be formed if neither the digits nor the letters are repeated?
