Statistics and Probability Problems with Solutions

Problems on statistics and probability are presented. The solutions to these problems are at the bottom of the page.

  1. Given the data set:

    \[4, 10, 7, 7, 6, 9, 3, 8, 9\]

    Find:

    1. the mode
    2. the median
    3. the mean
    4. the sample standard deviation
    5. If we replace the data value 6 by 24, will the standard deviation increase, decrease, or stay the same?

  2. Find \(x\) and \(y\) so that the ordered data set has a mean of 42 and a median of 35:

    \[17, 22, 26, 29, 34, x, 42, 67, 70, y\]

  3. Given the data set:

    \[62, 65, 68, 70, 72, 74, 76, 78, 80, 82, 96, 101\]

    Find:

    1. the median
    2. the first quartile
    3. the third quartile
    4. the interquartile range (IQR)

  4. The exam grades of 7 students are:

    \[70, 66, 72, 96, 46, 90, 50\]

    Find:

    1. the mean
    2. the sample standard deviation

  5. Twenty-four people had a blood test with results:

    \[A, B, B, AB, AB, B, O, O, AB, O, B, A\]

    \[AB, A, O, O, AB, B, O, A, AB, O, B, A\]

    1. Construct a frequency distribution for the data
    2. If a person is selected randomly, what is the probability that their blood type is not O?

  6. When a die is rolled and a coin is tossed, find the probability of obtaining:

    1. Tails and an even number
    2. A number greater than 3
    3. Heads or an odd number

  7. A box contains red and green balls. The number of green balls is \(\frac{1}{3}\) the number of red balls. If a ball is taken randomly from the box, what is the probability that the ball is red?

  8. The probability distribution of a random variable \(X\) is:

    \(x\)\(P(X = x)\)
    00.24
    10.38
    20.20
    30.13
    40.05

    Find the mean \(\mu\) and standard deviation \(\sigma\) of \(X\).

  9. A committee of 6 people is to be formed from 20 people, with women double the number of men. In how many ways can this be formed if there are 12 men?

  10. Calculate the mean \(\mu\) of the discrete data:

    \(x\)123456
    \(f\)2610622

  11. A student's marks in five tests are \(36\%\), \(78\%\), \(67\%\), \(88\%\), and \(98\%\). The weights are 1, 2, 2, 3, 3 respectively. Find the weighted mean \(\mu\).

  12. In a group of 40 people, 10 are healthy and the remaining 30 have high blood pressure, high cholesterol, or both. If 15 have high blood pressure and 25 have high cholesterol:

    1. How many people have both conditions?
    2. If a person is selected randomly, what is the probability that they:
      1. Have high blood pressure (event \(A\))?
      2. Have high cholesterol (event \(B\))?
      3. Have both conditions (event \(A \cap B\))?
      4. Have either condition (event \(A \cup B\))?
    3. Verify: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)

  13. A committee of 5 people is formed randomly from 10 women and 6 men. Find the probability that the committee has:

    1. 3 women and 2 men
    2. 4 women and 1 man
    3. 5 women
    4. At least 3 women

  14. In a school, \(60\%\) of pupils have internet access at home. A group of 8 students is chosen randomly. Find the probability that:

    1. Exactly 5 have access
    2. At least 6 have access

  15. The grades of 1000 students are normally distributed with mean \(\mu = 70\) and standard deviation \(\sigma = 10\). A student is selected randomly. Find:

    1. \(P(\text{grade} > 80)\)
    2. \(P(\text{grade} < 50)\)
    3. \(P(50 < \text{grade} < 80)\)
    4. Approximately how many students have grades > 80?

  16. In a country, 500 million tons of trash were recycled. The chart shows the distribution (in millions of tons).

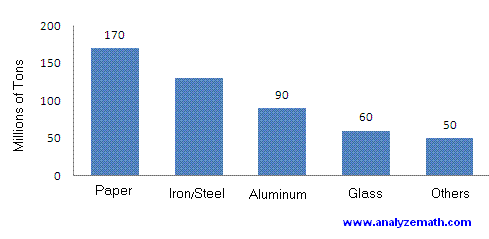
    recycling of products in millions of tons
    1. How many tons of Iron/Steel were recycled?
    2. What percentage of recycled trash was glass?

Solutions

    1. Mode: 7 and 9 (bimodal)
    2. Ordered: \(3, 4, 6, 7, 7, 8, 9, 9, 10\) → Median = 7
    3. Mean: \(\bar{x} = \frac{3+4+6+7+7+8+9+9+10}{9} = 7\)
    4. Sample standard deviation: \[ s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n-1}} = \sqrt{\frac{44}{8}} \approx 2.35 \]
    5. Standard deviation will increase because 24 is farther from the mean than 6.
  2. \(x = 36\), \(y = 77\)
    1. Median = 75
    2. First quartile \(Q_1 = 69\)
    3. Third quartile \(Q_3 = 81\)
    4. IQR = \(Q_3 - Q_1 = 12\)
    1. Mean = 70
    2. Sample standard deviation \(s \approx 18.6\)
    1. Blood TypeFrequency
      A5
      B6
      AB6
      O7
    2. \(P(\text{not O}) = 1 - \frac{7}{24} = \frac{17}{24} \approx 0.71\)
  6. Sample space has \(6 \times 2 = 12\) equally likely outcomes.
    1. \(P(\text{Tails and even}) = \frac{3}{12} = \frac{1}{4}\)
    2. \(P(\text{number} > 3) = \frac{6}{12} = \frac{1}{2}\)
    3. \(P(\text{Heads or odd}) = \frac{9}{12} = \frac{3}{4}\)
  7. Let \(R\) = number of red balls, \(G = \frac{1}{3}R\). Total balls = \(R + \frac{1}{3}R = \frac{4}{3}R\). \(P(\text{red}) = \frac{R}{\frac{4}{3}R} = \frac{3}{4}\)
  8. \[ \mu = \sum x \cdot P(X=x) = 0(0.24) + 1(0.38) + 2(0.20) + 3(0.13) + 4(0.05) = 1.37 \] \[ \sigma = \sqrt{\sum (x - \mu)^2 P(X=x)} \approx 1.13 \]
  9. Committee: 4 women, 2 men. Number of ways: \(\binom{8}{4} \times \binom{12}{2} = 70 \times 66 = 4620\)
  10. \[ \mu = \frac{\sum x_i f_i}{\sum f_i} = \frac{1(2)+2(6)+3(10)+4(6)+5(2)+6(2)}{28} \approx 3.21 \]
  11. \[ \text{Weighted mean} = \frac{36(1)+78(2)+67(2)+88(3)+98(3)}{1+2+2+3+3} = \frac{884}{11} = 80\% \]
    1. Let \(x\) = number with both. Then \((15-x)+(25-x)+x=30\) → \(x=10\)
      1. \(P(A) = \frac{15}{40} = 0.375\)
      2. \(P(B) = \frac{25}{40} = 0.625\)
      3. \(P(A \cap B) = \frac{10}{40} = 0.25\)
      4. \(P(A \cup B) = \frac{30}{40} = 0.75\)
    3. \(P(A)+P(B)-P(A \cap B) = 0.375+0.625-0.25 = 0.75 = P(A \cup B)\)
  13. Total ways: \(\binom{16}{5}\)
    1. \(P(3W,2M) = \frac{\binom{10}{3}\binom{6}{2}}{\binom{16}{5}} \approx 0.4121\)
    2. \(P(4W,1M) = \frac{\binom{10}{4}\binom{6}{1}}{\binom{16}{5}} \approx 0.2885\)
    3. \(P(5W) = \frac{\binom{10}{5}\binom{6}{0}}{\binom{16}{5}} \approx 0.0577\)
    4. \(P(\text{at least }3W) = 0.4121+0.2885+0.0577 \approx 0.7582\)
  14. Binomial with \(n=8\), \(p=0.6\)
    1. \(P(X=5) = \binom{8}{5}(0.6)^5(0.4)^3 \approx 0.2787\)
    2. \(P(X \geq 6) = P(X=6)+P(X=7)+P(X=8) \approx 0.3154\)
    1. \(z = \frac{80-70}{10} = 1\), \(P(Z > 1) = 1 - 0.8413 = 0.1587\)
    2. \(z = \frac{50-70}{10} = -2\), \(P(Z < -2) = 0.0228\)
    3. \(P(50 < X < 80) = 0.8413 - 0.0228 = 0.8185\)
    4. Number ≈ \(0.1587 \times 1000 \approx 159\) students
    1. Iron/Steel = \(500 - (170+90+60+50) = 130\) million tons
    2. Glass percentage = \(\frac{60}{500} \times 100\% = 12\%\)

More References and Links

Elementary Statistics and Probabilities
Home Page