This is a tutorial on the relationship between the amplitude, the vertical shift and the maximum and minimum of the sine function.
Problem 1
Function F is a sine function given bywith a > 0.
- Show that the maximum value Fmax and the minimum value Fmin of F(x) are given by
Fmax = d + a
Fmin = d - a
- Show that d = (Fmax + Fmin) / 2
- Show that a = (Fmax - Fmin) / 2
Solution to Problem 1:
- We start by using the fact that
-1 <= sin(bx + c) <= 1
- Multiply all terms of the above double inequality by a
-a <= sin(bx + c) <= a
- Add d to all terms of the double inequality above
d - a <= sin(bx + c) + d <= d + a
- sin(bx + c) + d is the expression that define F(x), hence
d - a <= F(x) <= d + a
- F(x) has a minimum value Fmin and a maximum value Fmax given by
Fmin = d - a
Fmax = d + a
- Add the left terms and the right terms of
Fmax = d + a and Fmin = d - a to obtain
Fmax + Fmin = 2d
- Divide both sides of the above by 2 to obtain
d = (Fmax + Fmin) / 2
- Add the left terms and the right terms of
Fmax = d + a and -Fmin = -d + a to obtain
Fmax - Fmin = 2a
- Divide both sides by 2 to obtain
a = (Fmax - Fmin) / 2
Problem 2
The graph of the sine function F given bywith a > 0, is shown below.
Use the graph and the results of problem 1 above to find a and d.
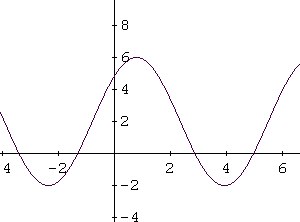
Solution to Problem 2:
- From the graph, the maximum value Fmax = 6 and the minimum value Fmin = -2, hence
d = (Fmax + Fmin) / 2 = 2
and
a = (Fmax - Fmin) / 2 = 4
More references and Links
Trigonometry Problems.Match Sine Functions to Graphs