Sine Functions: Maximum and Minimum – Problems

This tutorial explains the relationship between the amplitude, the vertical shift, and the maximum and minimum values of the sine function.

Problem 1

Function \( F \) is a sine function defined by

\[ F(x) = a\sin(bx + c) + d, \]

with \( a > 0 \).

Show that the maximum value \( F_{\max} \) and the minimum value \( F_{\min} \) of \( F(x) \) are \[ F_{\max} = d + a, \qquad F_{\min} = d - a. \]
Show that \[ d = \frac{F_{\max} + F_{\min}}{2}. \]
Show that \[ a = \frac{F_{\max} - F_{\min}}{2}. \]

Solution to Problem 1

We start by using the fact that \[ -1 \le \sin(bx + c) \le 1. \]
Multiply all terms of the above double inequality by \( a \): \[ -a \le a\sin(bx + c) \le a. \]
Add \( d \) to all terms of the inequality: \[ d - a \le a\sin(bx + c) + d \le d + a. \]
Since \( a\sin(bx + c) + d = F(x) \), we obtain \[ d - a \le F(x) \le d + a. \]
Therefore, the minimum and maximum values of \( F(x) \) are \[ F_{\min} = d - a, \qquad F_{\max} = d + a. \]
Add the equations \( F_{\max} = d + a \) and \( F_{\min} = d - a \): \[ F_{\max} + F_{\min} = 2d. \]
Divide both sides by 2 to obtain \[ d = \frac{F_{\max} + F_{\min}}{2}. \]
Add the equations \( F_{\max} = d + a \) and \( -F_{\min} = -d + a \): \[ F_{\max} - F_{\min} = 2a. \]
Divide both sides by 2 to obtain \[ a = \frac{F_{\max} - F_{\min}}{2}. \]

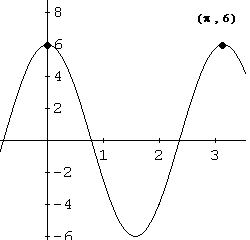
Problem 2

The graph of the sine function \( F \) defined by

\[ F(x) = a\sin(x) + d, \]

with \( a > 0 \), is shown below.

Use the graph and the results of Problem 1 to find \( a \) and \( d \).

Graph of a sine function showing maximum and minimum values

Solution to Problem 2

From the graph, the maximum value is \( F_{\max} = 6 \) and the minimum value is \( F_{\min} = -2 \).
Using the formulas from Problem 1: \[ d = \frac{F_{\max} + F_{\min}}{2} = \frac{6 + (-2)}{2} = 2, \] and \[ a = \frac{F_{\max} - F_{\min}}{2} = \frac{6 - (-2)}{2} = 4. \]

Problem 3

Find \( a \), \( b \), and \( c \) included in the definition of the sine function \( f \) given by

\[ f(x) = a \sin(bx + c) \]

such that the maximum value of \( f(x) \) is 6, \( f(0) = 6 \), and the period of the graph of function \( f \) is equal to \( \pi \). The constants \( a \), \( b \), and \( c \) are positive and \( c < 2\pi \).

Solution to Problem 3

The maximum value 6 gives the amplitude

\[ |a| = 6 \]
Solve the above equation for \( a \) and select the positive value.

\[ a = 6 \]
The period may be used to find \( b \) using

\[ \text{Period} = \frac{2\pi}{|b|} = \pi \]
Solve for \( |b| \)

\[ |b| = 2 \]
Solve for \( b \) and select the positive value

\[ b = 2 \]
Substitute 6 for \( a \) in the formula of the function and use \( f(0) = 6 \) to write an equation in \( c \).

\[ 6 = 6 \sin(2 \cdot 0 + c) \]
Which gives

\[ \sin(c) = 1 \]
Solve for \( c \)

\[ c = \frac{\pi}{2} + k(2\pi), \quad \text{where } k \text{ is an integer} \]
There is an infinite number of solutions for \( c \).
Select \( k = 0 \) since it is the only value that gives \( 0 < c < 2\pi \), which gives

\[ c = \frac{\pi}{2} \]
Function \( f \) is given by

\[ f(x) = 6 \sin\left(2x + \frac{\pi}{2}\right) \]
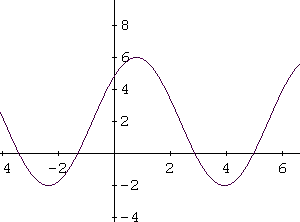
For checking, part of the graph of \( f \) is shown below. Check the period, verify that \( f(0) = 6 \), and confirm that the maximum value of \( f(x) \) is 6.