Trigonometric Functions of Acute Angles
\[ \sin x = \frac{\text{opp}}{\text{hyp}} = \frac{a}{c}, \quad \csc x = \frac{\text{hyp}}{\text{opp}} = \frac{c}{a} \] \[ \tan x = \frac{\text{opp}}{\text{adj}} = \frac{a}{b}, \quad \cot x = \frac{\text{adj}}{\text{opp}} = \frac{b}{a} \] \[ \cos x = \frac{\text{adj}}{\text{hyp}} = \frac{b}{c}, \quad \sec x = \frac{\text{hyp}}{\text{adj}} = \frac{c}{b} \]

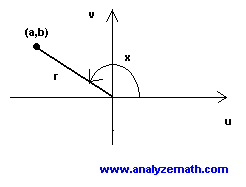
Trigonometric Functions of Arbitrary Angles
\[ \sin x = \frac{b}{r}, \quad \csc x = \frac{r}{b} \] \[ \tan x = \frac{b}{a}, \quad \cot x = \frac{a}{b} \] \[ \cos x = \frac{a}{r}, \quad \sec x = \frac{r}{a} \]
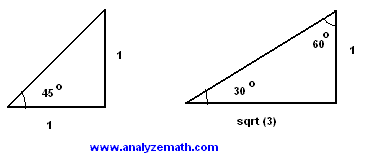
Special Triangles
Special triangles may be used to find trigonometric functions of special angles: 30°, 45°, and 60°.
Sine and Cosine Laws in Triangles
In any triangle we have:
1 - The sine law \[ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} \] 2 - The cosine laws \[ a^2 = b^2 + c^2 - 2bc \cos A \] \[ b^2 = a^2 + c^2 - 2ac \cos B \] \[ c^2 = a^2 + b^2 - 2ab \cos C \]

Relations Between Trigonometric Functions
\[ \csc x = \frac{1}{\sin x}, \quad \sin x = \frac{1}{\csc x} \] \[ \sec x = \frac{1}{\cos x}, \quad \cos x = \frac{1}{\sec x} \] \[ \tan x = \frac{1}{\cot x}, \quad \cot x = \frac{1}{\tan x} \] \[ \tan x = \frac{\sin x}{\cos x}, \quad \cot x = \frac{\cos x}{\sin x} \]
Pythagorean Identities
\[ \sin^2 x + \cos^2 x = 1 \] \[ 1 + \tan^2 x = \sec^2 x \] \[ 1 + \cot^2 x = \csc^2 x \]
Negative Angle Identities
\[ \sin(-x) = -\sin x, \quad \csc(-x) = -\csc x \] \[ \cos(-x) = \cos x, \quad \sec(-x) = \sec x \] \[ \tan(-x) = -\tan x, \quad \cot(-x) = -\cot x \]
Cofunction Identities
\[ \sin\left(\frac{\pi}{2} - x\right) = \cos x, \quad \cos\left(\frac{\pi}{2} - x\right) = \sin x \] \[ \tan\left(\frac{\pi}{2} - x\right) = \cot x, \quad \cot\left(\frac{\pi}{2} - x\right) = \tan x \] \[ \sec\left(\frac{\pi}{2} - x\right) = \csc x, \quad \csc\left(\frac{\pi}{2} - x\right) = \sec x \]
Addition and Subtraction Formulas
\[ \cos(x+y) = \cos x \cos y - \sin x \sin y, \quad \cos(x-y) = \cos x \cos y + \sin x \sin y \] \[ \sin(x+y) = \sin x \cos y + \cos x \sin y, \quad \sin(x-y) = \sin x \cos y - \cos x \sin y \] \[ \tan(x+y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}, \quad \tan(x-y) = \frac{\tan x - \tan y}{1 + \tan x \tan y} \] \[ \cot(x+y) = \frac{\cot x \cot y - 1}{\cot x + \cot y}, \quad \cot(x-y) = \frac{\cot x \cot y + 1}{\cot y - \cot x} \]
Sum-to-Product Formulas
\[ \cos x + \cos y = 2 \cos\frac{x+y}{2} \cos\frac{x-y}{2}, \quad \sin x + \sin y = 2 \sin\frac{x+y}{2} \cos\frac{x-y}{2} \]
Difference-to-Product Formulas
\[ \cos x - \cos y = -2 \sin\frac{x+y}{2} \sin\frac{x-y}{2}, \quad \sin x - \sin y = 2 \cos\frac{x+y}{2} \sin\frac{x-y}{2} \]
Product-to-Sum/Difference Formulas
\[ \cos x \cos y = \frac{1}{2}[\cos(x-y) + \cos(x+y)] \] \[ \sin x \cos y = \frac{1}{2}[\sin(x+y) + \sin(x-y)] \] \[ \cos x \sin y = \frac{1}{2}[\sin(x+y) - \sin(x-y)] \] \[ \sin x \sin y = \frac{1}{2}[\cos(x-y) - \cos(x+y)] \]
Difference of Squares Formulas
\[ \sin^2 x - \sin^2 y = \sin(x+y)\sin(x-y) \] \[ \cos^2 x - \cos^2 y = -\sin(x+y)\sin(x-y) \] \[ \cos^2 x - \sin^2 y = \cos(x+y)\cos(x-y) \]
Double Angle Formulas
\[ \sin(2x) = 2 \sin x \cos x, \quad \cos(2x) = 1 - 2 \sin^2 x = 2 \cos^2 x - 1 \] \[ \tan(2x) = \frac{2 \tan x}{1 - \tan^2 x} \]
Multiple Angle Formulas
\[ \sin(3x) = 3\sin x - 4 \sin^3 x, \quad \cos(3x) = 4\cos^3 x - 3\cos x \] \[ \sin(4x) = 4 \sin x \cos x - 8 \sin^3 x \cos x, \quad \cos(4x) = 8 \cos^4 x - 8 \cos^2 x + 1 \]
Half Angle Formulas
\[ \sin \frac{x}{2} = \pm \sqrt{\frac{1-\cos x}{2}}, \quad \cos \frac{x}{2} = \pm \sqrt{\frac{1+\cos x}{2}} \] \[ \tan \frac{x}{2} = \pm \sqrt{\frac{1-\cos x}{1+\cos x}} = \frac{\sin x}{1+\cos x} = \frac{1-\cos x}{\sin x} \]
Power Reducing Formulas
\[ \sin^2 x = \frac{1}{2} - \frac{1}{2}\cos(2x), \quad \cos^2 x = \frac{1}{2} + \frac{1}{2}\cos(2x) \] \[ \sin^3 x = \frac{3}{4} \sin x - \frac{1}{4} \sin(3x), \quad \cos^3 x = \frac{3}{4} \cos x + \frac{1}{4} \cos(3x) \] \[ \sin^4 x = \frac{3}{8} - \frac{1}{2}\cos(2x) + \frac{1}{8}\cos(4x), \quad \cos^4 x = \frac{3}{8} + \frac{1}{2}\cos(2x) + \frac{1}{8}\cos(4x) \]
Trigonometric Functions Periodicity
\[ \sin(x+2\pi) = \sin x, \quad \cos(x+2\pi) = \cos x \] \[ \sec(x+2\pi) = \sec x, \quad \csc(x+2\pi) = \csc x \] \[ \tan(x+\pi) = \tan x, \quad \cot(x+\pi) = \cot x \]