Rhombus Problems
Rhombus problems with detailed solutions are presented. Rhombus Calculator and Solver also included.
Definition of a Rhombus
The rhombus is a parallelogram with four congruent sides (sides with equal lengths). A square is a special case of a rhombus.

Properties of a Rhombus
These are some of the most important properties of a rhombus.
Consider the rhombus ABCD shown in the figure above.
1 - All sides are congruent (equal lengths).
length AB = length BC = length CD = length DA = a.
2 - Opposite sides are parallel.
AD is parallel to BC and AB is parallel to DC.
3 - The two diagonals are perpendicular.
AC is perpendicular to BD.
4 - Opposite internal angles are congruent (equal sizes).
internal angle A = internal angle C
and
internal angle B = internal angle D.
5 - Any two consecutive internal angles are supplementary : they add up to 180 degrees.
angle A + angle B = 180 degrees
angle B + angle C = 180 degrees
angle C + angle D = 180 degrees
angle D + angle A = 180 degrees
Area of a Rhombus
These are three formulas for the area of the rhombus.
Formula 1
area = a × h , where a is the side length of the rhombus and h is the perpendicular distance between two parallel sides of the rhombus.
Formula 2
area = a 2 sin (A) = a 2 sin (B). Since angles A and B are supplementary angles, sin (A) = sin (B).
Formula 3
area = (1/2) d1 d2, where d1 and d2 are the lengths of the two diagonals.
Problems on Rhombus with Detailed Solutions
Problem 1
The size of the obtuse angle of a rhombus is twice the size of its acute angle. The side length of the rhombus is equal to 10 feet. Find the area of the rhombus.
Solution to Problem 1:
- A rhombus has 2 congruent opposite acute angles and two congruent opposite obtuse angles. One of the properties of a rhombus is that any two internal consecutive angles are supplementary. Let x be the acute angle. The obtuse angle is twice: 2x. Which gives the following equation.
x + 2 x = 180 degrees.
- Solve the above equation for x.
3x = 180 degrees.
x = 60 degrees.
- We use formula 2 for the area of a rhombus knowing the side length and one of the angles.
area of rhombus = (10 feet) 2 sin (60 degrees)
= 86.6 feet 2 (rounded to 1 decimal place)
Problem 2
The lengths of the diagonals of a rhombus are 20 and 48 meters. Find the perimeter of the rhombus.
Solution to Problem 2:
- Below is shown a rhombus with the given diagonals. Consider the right triangle BOC and apply the Pythagorean theorem as follows

BC 2 = 10 2 + 24 2
- and evaluate BC
BC = 26 meters.
- We now evaluate the perimeter P as follows:
P = 4 * 26 = 104 meters.
Problem 3
The perimeter of a rhombus is 120 feet and one of its diagonal has a length of 40 feet. Find the area of the rhombus.
Solution to Problem 3:
- All 4 sides of a rhombus are equal. Hence, a perimeter of 120 ft when divided by 4 gives the side of the rhombus 30 feet. Hence
BC = 30 ft
- The length of the side OC of the right triangle is equal to half the diagonal: 20 feet.
OC = 20 ft
Let us now consider the right triangle BOC and apply the Pythagorean theorem to find the length of side BO.
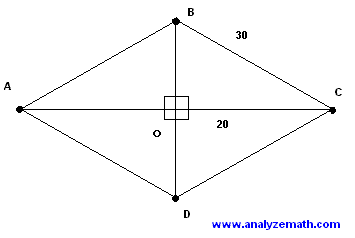
BC 2 = BO 2 +OC 2
Substitute
30 2 = BO 2 + 20 2
BO = 10 √(5) feet
- We now calculate the area of the right triangle BOC and multiply it by 4 to obtain the area of the rhombus.
area = 4 ( 1/2) BO OC = 4 (1/2)10 √ (5) 20
= 400 √(5) feet 2
More References and Links to Geometry
Geometry Tutorials, Problems and Interactive Applets.
Rhombus - Geometry Calculator to calculate the characteristics of a rhombus



