Sectors and Circles Problems
Problems on sectors and circles with detailed solutions.
Problem 1
In the figure below, the length of arc AB is equal to twice the length of radius r of the circle. Find the area of sector OAB in terms of the radius r.
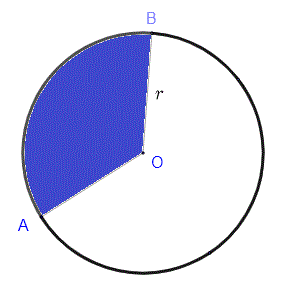
Solution to Problem 1:
- The formula for the arc length is given by
arc length AB = r * angle AOB
- arc length AB is given and is equal to 2r, hence
2r = r * angle AOB
- Solve for angle AOB to obtain
angle AOB = 2 radians
- The area of the sector is given by
Area = (1/2) * angle AOB * r 2 = (1/2) * 2 * r 2 = r 2
Problem 2
The angle of a sector in a given circle is 40 degrees and the area of the sector is equal to 20 cm 2. Calculate the arc length of the sector.
Solution to Problem 2:
- The formula for the area of a sector is
Area = (1 / 2) * angle of sector * r 2
- The area and the angle are given. The angle is given in degrees and has to be converted into radians.
20 = (1 / 2) (40 Pi / 180) * r 2
- Solve for radius r to obtain
r = square root [ 2 * 20 * 180 / (40 Pi) ]
= square root [ 180 / Pi ]
- The arc length is given by
arc length of sector = angle of sector * r
= [ 40 * Pi / 180 ] * square root [ 180 / Pi ]
= [ Pi / 4.5 ] * square root [ 180 / Pi ] = 5.3 cm (rounded to 1 decimal place)
Problem 3
In the figure below, AB and DC are arcs of concentric circles with center O. The perimeter of figure ABCD is 22 cm. Calculate
a) angle AOB
b) The area of figure ABCD.

Solution to Problem 3:
- The perimeter of ABCD is given by
perimeter = arc AB + 6 + arc DC + 6 = 22
- If we let x be the size of the sector central angle, arc AB and arc DC are given by (formula for arc length of sector)
arc AB = 2 * x and arc DC = 8 * x
- Substitute in the above perimeter formula
2x + 6 + 8x + 6 = 22
- Solve for x
x = 1 radian
- The area of figure ABCD is found by subtracting the area of the small sector from the area of the larger sector
area of ABCD = (1 / 2) 8 2 * 1 - (1 / 2) 2 2 * 1
= 30 cm 2
More References and Links to Geometry Tutorials and Problems
Geometry Tutorials, Problems and Interactive Applets.
Triangle Problems


