Similar Triangles Examples and Problems with Solutions

Definitions and theorems related to similar triangles are discussed using examples. Also examples and problems with detailed solutions are included.

Review of Similar Triangles

Definition

Two triangles ABC and A'B'C' are similar if the three angles of the first triangle are congruent to the corresponding three angles of the second triangle and the lengths of their corresponding sides are proportional as follows.
AB / A'B' = BC / B'C' = CA / C'A'
definition of similar triangles.

Angle-Angle (AA) Similarity Theorem

If two angles in a triangle are congruent to the two corresponding angles in a second triangle, then the two triangles are similar.
Example 1
Let ABC be a triangle and A'C' a segment parallel to AC. What can you say about triangles ABC and A'BC'? Explain your answer.
Angle-Angle similarity

Solution to Example 1

Since A'C' is parallel to AC, angles BA'C' and BAC are congruent. Also angles BC'A' and BCA are congruent. Since the two triangles have two corresponding congruent angles, they are similar.

Side-Side-Side (SSS) Similarity Theorem

If the three sides of a triangle are proportional to the corresponding sides of a second triangle, then the triangles are similar.
Example 2
Let the vertices of triangles ABC and PQR defined by the coordinates: A(-2,0), B(0,4), C(2,0), P(-1,1), Q(0,3), and R(1,1). Show that the two triangles are similar.

Solution to Example 2

Let us first plot the vertices and draw the triangles.
Since we know the coordinates of the vertices, we can find the length of the sides of the two triangles.
AB = √ ( 4² + 2² ) = 2 √5
BC = √ ( (-4)² + 2² ) = 2 √5
CA = √ ( 4² ) = 4
PQ = √ ( 2² + 1² ) = √5
QR = √ ( (-2)² + 1² ) = √5
RP = √ ( 2² ) = 2
We now calculate the ratios of the lengths of the corresponding sides.
AB / PQ = 2 , BC / QR = 2 and CA / RP = 2
We can now write.
AB / PQ = BC / QR = CA / RP = 2
The lengths of the corresponding sides are proportional and therefore the two triangles are similar.

Side-Angle-Side (SAS) Similarity Theorem

If an angle of a triangle is congruent to the corresponding angle of a second triangle, and the lengths of the two sides including the angle in one triangle are proportional to the lengths of the corresponding two sides in the second triangle, then the two triangles are similar.
Example 3
Show that triangles ABC and A'BC', in the figure below, are similar.
Side-Angle-Side (SAS) similarity

Solution to Example 3

Angles ABC and A'BC' are congruent.
Since the lengths of the sides including the congruent angles are given, let us calculate the ratios of the lengths of the corresponding sides.
BA / BA' = 10 / 4 = 5 / 2
BC / BC' = 5 / 2
The two triangles have two sides whose lengths are proportional and a congruent angle included between the two sides. The two triangles are similar.

Similar Triangles Problems with Solutions

Problems 1
In the triangle ABC shown below, A'C' is parallel to AC. Find the length y of BC' and the length x of A'A.
similar triangles problem 1

Solution to Problem 1

BA is a transversal that intersects the two parallel lines A'C' and AC, hence the corresponding angles BA'C' and BAC are congruent. BC is also a transversal to the two parallel lines A'C' and AC and therefore angles BC'A' and BCA are congruent. These two triangles have two congruent angles are therefore similar and the lengths of their sides are proportional. Let us separate the two triangles as shown below.
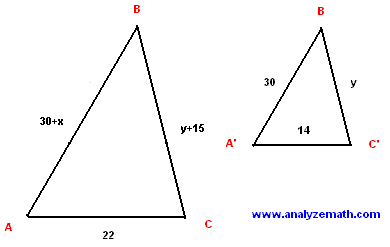
We now use the proportionality of the lengths of the side to write equations that help in solving for x and y.
(30 + x) / 30 = 22 / 14 = (y + 15) / y
An equation in x may be written as follows.
(30 + x) / 30 = 22 / 14
Solve the above for x.
420 + 14 x = 660
x = 17.1 (rounded to one decimal place).
An equation in y may be written as follows.
22 / 14 = (y + 15) / y
Solve the above for y to obtain.
y = 26.25

Problems 2
A research team wishes to determine the altitude of a mountain as follows (see figure below): They use a light source at L, mounted on a structure of height 2 meters, to shine a beam of light through the top of a pole P' through the top of the mountain M'. The height of the pole is 20 meters. The distance between the altitude of the mountain and the pole is 1000 meters. The distance between the pole and the laser is 10 meters. We assume that the light source mount, the pole and the altitude of the mountain are in the same plane. Find the altitude h of the mountain.

Solution to Problem 2

We first draw a horizontal line LM. PP' and MM' are vertical to the ground and therefore parallel to each other. Since PP' and MM' are parallel, the triangles LPP' and LMM' are similar. Hence the proportionality of the sides gives:
1010 / 10 = (h - 2) / 18
Solve for h to obtain
h = 1820 meters.

Problems 3
The two triangles are similar and the ratio of the lengths of their sides is equal to k: AB / A'B' = BC / B'C' = CA / C'A' = k. Find the ratio BH / B'H' of the lengths of the altitudes of the two triangles.

Solution to Problem 3

If the two triangles are similar, their corresponding angles are congruent. Hence angle BAH and B'A'H are congruent. We now examine the triangles BAH and B'A'H'. These triangles have two pairs of corresponding congruent angles: BAH and B'A'H' and the right triangles BHA and B'H'A'. The triangles are similar and therefore:
AB / A'B' = BH / B'H' = k

Problems 4
BA' and AB' are chords of a circle that intersect at C. Find a relationship between the lengths of segments AC, BC, B'C and A'C.

intersecting chords inside a circle problem 4

Solution to Problem 4

We first join points B and A and B' and A'. Angles ABA' and AB'A' in the the two triangles are congruent since they intercept the same arc. Angles BAB' and BA'B' also intercept the same arc and therefore congruent. The two triangles ABC and A'B'C have two corresponding congruent angles and are therefore similar.
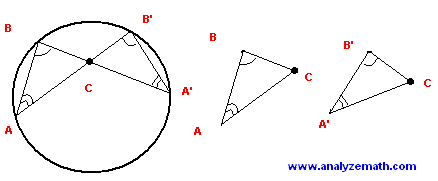
Before we write the proportionality of the sides, we first separate the two triangles and identify the corresponding sides then write the proportionality of the lengths of the sides.
AB / A'B' = BC / B'C = CA / CA'
Since we are looking for a relationship between the lengths of AC, BC, B'C and A'C, we therefore use the last equation and cross product it to obtain
BC * CA' = B'C * CA

Problems 5
ABC is a right triangle. AM is perpendicular from vertex A to the hypotenuse BC of the triangle. How many similar triangles are there?

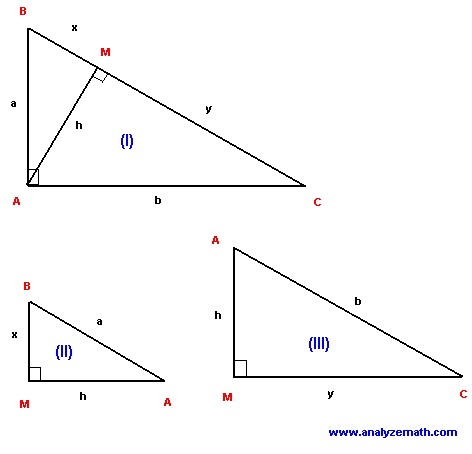
Solution to Problem 5

Consider triangles ABC and MBA. They have two corresponding congruent angles: the right angle and angle B. They are similar. Also triangles ABC and MAC have two congruent angles: the right angle and angle C. Therefore there are three similar triangles: ABC, MBA and MAC.