Points of Intersection of a Hyperbola and a Line
This tutorial explains how to find the points of intersection of a
hyperbola
and a
line
given by their equations.
Example 1
Find the points of intersection of a hyperbola and a line given by the equations:
\[
\frac{x^2}{9} - y^2 = 1
\]
\[
x + 5y = 3
\]
Solution
-
Solve the equation of the line for \(x\):
\[
x = 3 - 5y
\]
-
Substitute \(x = 3 - 5y\) into the equation of the hyperbola:
\[
\frac{(3 - 5y)^2}{9} - y^2 = 1
\]
-
Expand and simplify:
\[
\frac{9 - 30y + 25y^2}{9} - y^2 = 1
\]
which simplifies to
\[
16y^2 - 30y = 0
\]
-
Solve the quadratic equation:
\[
16y^2 - 30y = 0
\]
\[
y(16y - 30) = 0
\]
giving the two solutions
\[
y = 0 \quad \text{and} \quad y = \frac{15}{8}
\]
-
Substitute these values into \(x = 3 - 5y\):
-
For \(y = 0\):
\[
x = 3
\]
-
For \(y = \frac{15}{8}\):
\[
x = 3 - 5\left(\frac{15}{8}\right) = -\frac{51}{8}
\]
-
Therefore, the points of intersection are:
\[
(3,\,0) \quad \text{and} \quad \left(-\frac{51}{8},\,\frac{15}{8}\right)
\]
The graph below shows the hyperbola, the line, and their points of intersection.
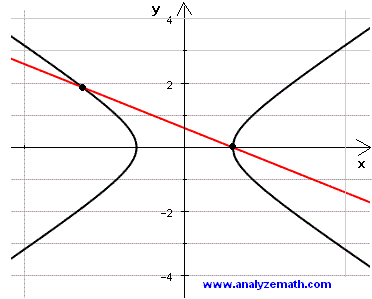
More References on Hyperbolas
