AP Calculus AB Practice Test: 20 Sample Questions

A collection of challenging AP Calculus AB questions similar to those on the actual exam. Detailed solutions and explanations are available. Answers are provided at the bottom of the page.

1. \[ \lim_{h \to 0} \frac{e^{4} e^{h} - e^{4}}{h} = \]

   A) \(e\)
   B) \(1\)
   C) \(e^h\)
   D) \(e^4\)
   E) \(4^e\)

2. The function \(g\) defined by \[ g(x) = \frac{x^{3} + 2x^{2} - 3x}{x^{2} + 2x - 3} \] has vertical asymptotes at:

   A) \(x = 1, -3\)
   B) \(x = 0\)
   C) \(x = 1\)
   D) \(x = -3\)
   E) Function \(g\) has no vertical asymptotes

3. Given \[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \] find \[ \lim_{x \to 0} \frac{x + 4x^{2} + \sin x}{3x} \]

   A) \(\frac{2}{3}\)
   B) \(\frac{4}{3}\)
   C) \(\frac{1}{3}\)
   D) \(2\)
   E) Does not exist

4. Function \(f\) is defined by \[ f(x) = 2x^{3}\sin(x) + \frac{1}{x}\tan(x) + x\sec(x) + 2 \] find \(f'(x)\).

   A) \(6x^2 \sin(x) - \frac{1}{x^2}\tan(x) + \sec(x)\)
   B) \(6x^2 \sin(x) + 2x^3 \cos(x) - \frac{1}{x^2}\tan(x) + \frac{1}{x} \sec^2(x) + \sec(x) + x \sin(x) \sec^2(x)\)
   C) \(2x^3 \cos(x) + \frac{1}{x} \sec^2(x) + x \sin(x) \sec^2(x)\)
   D) \(6x^2 \cos(x) - \frac{1}{x^2} \sec^2(x) + \sec^2(x)\)
   E) \(6x^2 \sin(x) + 2x^3 \cos(x) - \frac{1}{x^2}\tan(x) + \frac{1}{x} \sec^2(x) + \sec(x) + x \sin(x) \sec^2(x) + 2\)

5. Curve \(C\) is described by \(0.25x^2 + y^2 = 9\). Determine the \(y\)-coordinates where the tangent line has slope \(1\).

   A) \(-\frac{3\sqrt{5}}{5}, \frac{3\sqrt{5}}{5}\)
   B) \(-\frac{\sqrt{35}}{2}, \frac{\sqrt{35}}{2}\)
   C) \(-3, 3\)
   D) \(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\)
   E) \(-3\sqrt{2}, 3\sqrt{2}\)

6. Solve the differential equation \(\frac{dy}{dx} = \frac{\cos x}{y^2}\) with \(y(\pi/2) = 0\).

   A) \(y = 3 \sin x - 3\)
   B) \(y = \sin x - 1\)
   C) \(y = \sqrt[3]{3 \sin x - 3}\)
   D) \(y = (3 \sin x - 3)^3\)
   E) \(y = \frac{1}{\sqrt[3]{3 \sin x - 3}}\)

7. \[ \int \sin^4 x \cos x \, dx = \]

   A) \(\cos^5 x + C\)
   B) \(-\frac{1}{5}\sin^5 x + C\)
   C) \(\sin^5 x + C\)
   D) \(-\frac{1}{5}\cos^5 x + C\)
   E) \(-5\cos^5 x + C\)

8. \[ \frac{d}{dx} \int_{3}^{2x} \sin(t^2 + 1) \, dt = \]

   A) \(2 \sin(4x^2 + 1)\)
   B) \(2 \sin(x^2 + 1)\)
   C) \(\sin(x^2 + 1)\)
   D) \(2 \sin(4x^2 + 1) - 2 \sin(3^2 + 1)\)
   E) \(2 \sin(4x^2)\)

9. \[ \int_{0}^{10} \left(|4 - x| + |2 - 2x|\right)dx = \]

   A) \(100\)
   B) \(108\)
   C) \(110\)
   D) \(112\)
   E) \(114\)

10. \[ \int \frac{(5 + x^{3/4})^{9}}{x^{1/4}}dx = \]

    A) \((5 + x^{3/4})^{10}\)
    B) \((x^{3/4})^{10}\)
    C) \(\frac{1}{10}(5 + x^{3/4})^{10}\)
    D) \(\frac{1}{10} \frac{(5 + x^{3/4})^{10}}{x^{1/4}}\)
    E) \(\frac{2}{15}(5 + x^{3/4})^{10}\)

11. Given \[ h(x) = (\arctan(x^3 + 1) + 2x)^4\], find \(h'(x)\).

    A) \(\frac{3x^2}{x^6 + 2x^3 + 2} + 2\)
    B) \(4(\arctan(x^3 + 1) + 2x)^3 \cdot \left( \frac{3x^2}{x^6 + 2x^3 + 2} \right)\)
    C) \(4(\arctan(x^3 + 1) + 2x)^3\)
    D) \(4(\arctan(x^3 + 1) + 2x)^3 \cdot \left( \frac{3x^2}{x^6 + 2x^3 + 2} + 2 \right)\)
    E) \(\frac{1}{4}(\arctan(x^3 + 1) + 2x)^3\)

12. The graph of function \(h\) is shown below. How many zeros does \(h'\) have?

    

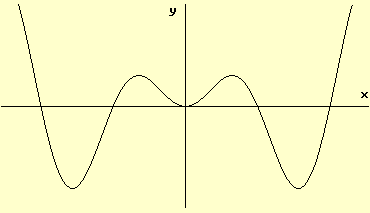
    A) \(1\)
    B) \(2\)
    C) \(3\)
    D) \(4\)
    E) \(5\)

13. The graph of a polynomial \(f\) is shown. If we divide \(f'(x)\) by \(x - b\), the remainder is most likely:

    

    A) \(f(b)\)
    B) \(1\)
    C) \(0\)
    D) \(2\)
    E) \(-1\)

14. The parametric curve \((\ln(t - 2), 3t)\) for \(t > 2\) represents:

    A) \(y = \ln\left(\frac{x}{3} - 2\right)\)
    B) \(y = 3x\)
    C) \(x = \ln(y - 2)\)
    D) \(y = 3(e^x + 2)\)
    E) \(y = \ln(x)\)

15. Let \(P(x) = 2x^3 + Kx + 1\). Find \(K\) if the remainder when dividing \(P(x)\) by \(x - 2\) is \(10\).

    A) \(-\frac{7}{2}\)
    B) \(\frac{2}{7}\)
    C) \(\frac{7}{2}\)
    D) \(-\frac{2}{7}\)
    E) \(K\) cannot be determined

16. Function \(f\) is defined by: \[ f(x) = \begin{cases} f(x) = \dfrac{\sqrt{4x + 4} - \sqrt{2x + 4}}{2x}, \\\\ f(0) = C \end{cases} \] What value of \(C\) makes \(f\) continuous at \(x = 0\)?

    A) \(0\)
    B) \(\frac{1}{4}\)
    C) \(\frac{1}{8}\)
    D) \(1\)
    E) Any real number

17. Given \(f'(x) = g(x)\) and \(g'(x) = f(x)\), the second derivative of \((f \cdot g)(x)\) is:

    A) \(f''(x)g''(x)\)
    B) \(g'(x)g(x) + f(x)f'(x)\)
    C) \(4g(x)f(x)\)
    D) \(2g(x)f(x)\)
    E) \(g(x)f(x)\)

18. The average rate of change of \(f(x) = \sin x + x\) on \([0, \pi]\) is:

    A) \(0\)
    B) \(2\pi\)
    C) \(\pi\)
    D) \(2\)
    E) \(1\)

19. Find the area of the shaded region between \(y = \sin x\) and \(y = \frac{1}{2}\):

    

    A) \(1\)
    B) \(0.5\)
    C) \(2 + \frac{\pi}{3}\)
    D) \(2 + \frac{\pi}{3} - \sqrt{3}\)
    E) \(2 + \frac{\pi}{3} + \sqrt{3}\)

20. Given \(g(x) = f(x^2)\), \(f(x) = h(x^3 + 1)\), and \(h'(x) = 2x + 1\), find \(g'(x)\).

    A) \(2x^3\)
    B) \(12x^9 + 18x^3\)
    C) \(2x^{11} + 3x^5\)
    D) \(2x^9 + 3x^3\)
    E) \(12x^{11} + 18x^5\)