Question
Evaluate the limit:
\[ \lim_{h \to 0} \frac{e^{4} e^{h} - e^{4}}{h} \]Solution
As \(h \to 0\), direct substitution gives the indeterminate form \( \frac{0}{0} \).
Let \( f(x) = e^{x} \). The limit can be rewritten as:
\[ \lim_{h \to 0} \frac{e^{4+h} - e^{4}}{h} = \lim_{h \to 0} \frac{f(4+h) - f(4)}{h} \]This is the definition of the derivative of \( f(x) = e^{x} \) at \(x = 4\). Therefore,
\[ \lim_{h \to 0} \frac{e^{4} e^{h} - e^{4}}{h} = f'(4) = e^{4} \]Question
The function \(g\) defined by
\[ g(x) = \frac{x^{3} + 2x^{2} - 3x}{x^{2} + 2x - 3} \]has vertical asymptotes at:
Solution
Factor and simplify the rational function:
\[ g(x) = \frac{x(x^{2} + 2x - 3)}{x^{2} + 2x - 3} = x \]The simplified function \(g(x) = x\) has no vertical asymptotes.
Question
Given
\[ \lim_{x \to 0} \frac{\sin x}{x} = 1 \]find
\[ \lim_{x \to 0} \frac{x + 4x^{2} + \sin x}{3x} \]Solution
Using the limit sum rule:
\[ \begin{aligned} \lim_{x \to 0} \frac{x + 4x^{2} + \sin x}{3x} &= \lim_{x \to 0} \left( \frac{x}{3x} + \frac{4x^{2}}{3x} + \frac{\sin x}{3x} \right) \\ &= \lim_{x \to 0} \frac{1}{3} + \lim_{x \to 0} \frac{4x}{3} + \frac{1}{3} \lim_{x \to 0} \frac{\sin x}{x} \\ &= \frac{1}{3} + 0 + \frac{1}{3}(1) = \frac{2}{3} \end{aligned} \]Question
Function \(f\) is defined by
\[ f(x) = 2x^{3}\sin(x) + \frac{1}{x}\tan(x) + x\sec(x) + 2 \]Find \(f'(x)\).
Solution
Differentiate term by term:
\[ \begin{aligned} f'(x) &= \frac{d}{dx}[2x^{3}\sin(x)] + \frac{d}{dx}\left[\frac{1}{x}\tan(x)\right] + \frac{d}{dx}[x\sec(x)] + \frac{d}{dx}[2] \\[4pt] &= 2[3x^{2}\sin(x) + x^{3}\cos(x)] + \left[-\frac{1}{x^{2}}\tan(x) + \frac{1}{x}\sec^{2}(x)\right] + [\sec(x) + x\sin(x)\sec^{2}(x)] + 0 \\[4pt] &= 6x^{2}\sin(x) + 2x^{3}\cos(x) - \frac{1}{x^{2}}\tan(x) + \frac{1}{x}\sec^{2}(x) + \sec(x) + x\sin(x)\sec^{2}(x) \end{aligned} \]Question
Curve \(C\) is described by \(0.25x^{2} + y^{2} = 9\). Determine the \(y\)-coordinates of points on \(C\) where tangent lines have slope \(1\).
Solution
Implicit differentiation:
\[ 0.5x + 2y y' = 0 \Rightarrow y' = -\frac{0.5x}{2y} = -\frac{x}{4y} \]Set \(y' = 1\):
\[ -\frac{x}{4y} = 1 \Rightarrow x = -4y \]Substitute into original equation:
\[ 0.25(-4y)^{2} + y^{2} = 9 \Rightarrow 4y^{2} + y^{2} = 9 \Rightarrow 5y^{2} = 9 \Rightarrow y = \pm\frac{3\sqrt{5}}{5} \]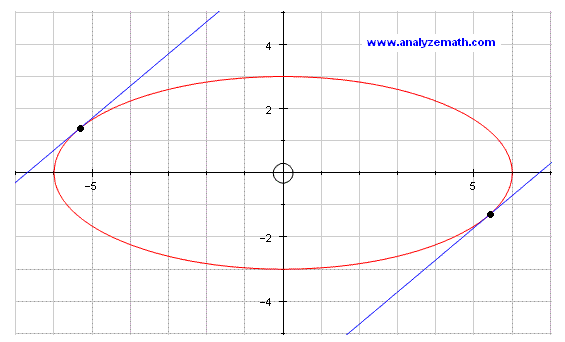
Question
Solve the differential equation:
\[ \frac{dy}{dx} = \frac{\cos x}{y^{2}}, \quad y\left(\frac{\pi}{2}\right) = 0 \]Solution
Separate variables:
\[ y^{2} \, dy = \cos x \, dx \]Integrate both sides:
\[ \int y^{2} \, dy = \int \cos x \, dx \Rightarrow \frac{1}{3}y^{3} = \sin x + C \]Apply initial condition \(y(\pi/2) = 0\):
\[ \frac{1}{3}(0)^{3} = \sin\left(\frac{\pi}{2}\right) + C \Rightarrow 0 = 1 + C \Rightarrow C = -1 \]Solve for \(y\):
\[ \frac{1}{3}y^{3} = \sin x - 1 \Rightarrow y^{3} = 3(\sin x - 1) \Rightarrow y = \sqrt[3]{3\sin x - 3} \]Question
Evaluate:
\[ \int \sin^{4} x \cos x \, dx \]Solution
Use substitution \(u = \sin x\), \(du = \cos x \, dx\):
\[ \int \sin^{4} x \cos x \, dx = \int u^{4} \, du = \frac{1}{5}u^{5} + C = \frac{1}{5}\sin^{5} x + C \]Question
Find:
\[ \frac{d}{dx} \int_{3}^{2x} \sin(t^{2} + 1) \, dt \]Solution
Apply the Fundamental Theorem of Calculus with chain rule:
\[ \frac{d}{dx} \int_{3}^{2x} \sin(t^{2} + 1) \, dt = \sin((2x)^{2} + 1) \cdot \frac{d}{dx}(2x) = 2\sin(4x^{2} + 1) \]Question
Evaluate:
\[ \int_{0}^{10} \left(|4 - x| + |2 - 2x|\right) \, dx \]Solution
Break at points where expressions change sign: \(x = 4\) for \(|4-x|\) and \(x=1\) for \(|2-2x|\):
\[ \begin{aligned} \int_{0}^{10} |4-x| \, dx &= \int_{0}^{4} (4-x) \, dx + \int_{4}^{10} (x-4) \, dx = 8 + 18 = 26 \\[4pt] \int_{0}^{10} |2-2x| \, dx &= \int_{0}^{1} (2-2x) \, dx + \int_{1}^{10} (2x-2) \, dx = 1 + 81 = 82 \end{aligned} \]Sum the results:
\[ 26 + 82 = 108 \]Question
Evaluate:
\[ \int \frac{(5 + x^{3/4})^{9}}{x^{1/4}} \, dx \]Solution
Use substitution \(u = 5 + x^{3/4}\), \(du = \frac{3}{4}x^{-1/4} \, dx\):
\[ \int \frac{(5 + x^{3/4})^{9}}{x^{1/4}} \, dx = \frac{4}{3} \int u^{9} \, du = \frac{4}{3} \cdot \frac{u^{10}}{10} + C = \frac{2}{15}(5 + x^{3/4})^{10} + C \]Question
Given \(h(x) = [\arctan(x^{3} + 1) + 2x]^{4}\), find \(h'(x)\).
Solution
Apply chain rule:
\[ \begin{aligned} h'(x) &= 4[\arctan(x^{3}+1) + 2x]^{3} \cdot \frac{d}{dx}[\arctan(x^{3}+1) + 2x] \\ &= 4[\arctan(x^{3}+1) + 2x]^{3} \cdot \left[ \frac{3x^{2}}{1 + (x^{3}+1)^{2}} + 2 \right] \\ &= 4[\arctan(x^{3}+1) + 2x]^{3} \cdot \frac{3x^{2} + 2(x^{6} + 2x^{3} + 2)}{x^{6} + 2x^{3} + 2} \end{aligned} \]Question
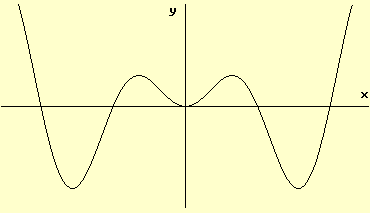
The graph of function \(h\) is shown. How many zeros does \(h'\) have?
Solution
\(h'(x) = 0\) at local extrema. The graph shows 3 local minima and 2 local maxima, so \(h'\) has 5 zeros.
Question
The graph of polynomial \(f\) is shown. If \(f'\) is its derivative, the remainder of \(f'(x) \div (x-b)\) is:

Solution
Since \(f\) has a local maximum at \(x = b\), \(f'(b) = 0\). By the Remainder Theorem, the remainder when \(f'(x)\) is divided by \((x-b)\) is \(f'(b) = 0\).
Question
The set of all points \((\ln(t-2), 3t)\), \(t > 2\), is the graph of:
Solution
From parametric equations: \(x = \ln(t-2)\), \(y = 3t\). Solve for \(t\) from \(y\): \(t = y/3\). Substitute into \(x\):
\[ x = \ln\left(\frac{y}{3} - 2\right) \Rightarrow e^{x} = \frac{y}{3} - 2 \Rightarrow y = 3(e^{x} + 2) \]Question
Let \(P(x) = 2x^{3} + Kx + 1\). Find \(K\) if the remainder of \(P(x) \div (x-2)\) is 10.
Solution
By Remainder Theorem: \(P(2) = 10\):
\[ 2(2)^{3} + K(2) + 1 = 10 \Rightarrow 16 + 2K + 1 = 10 \Rightarrow 2K = -7 \Rightarrow K = -\frac{7}{2} \]Question
Function \(f\) is defined by:
\[ f(x) = \begin{cases} \dfrac{\sqrt{4x+4} - \sqrt{2x+4}}{2x}, & x \neq 0 \\[6pt] C, & x = 0 \end{cases} \]Find \(C\) for continuity at \(x=0\).
Solution
Rationalize numerator:
\[ \begin{aligned} \lim_{x \to 0} f(x) &= \lim_{x \to 0} \frac{(\sqrt{4x+4} - \sqrt{2x+4})(\sqrt{4x+4} + \sqrt{2x+4})}{2x(\sqrt{4x+4} + \sqrt{2x+4})} \\ &= \lim_{x \to 0} \frac{(4x+4) - (2x+4)}{2x(\sqrt{4x+4} + \sqrt{2x+4})} \\ &= \lim_{x \to 0} \frac{2x}{2x(\sqrt{4x+4} + \sqrt{2x+4})} = \frac{1}{\sqrt{4}+\sqrt{4}} = \frac{1}{4} \end{aligned} \]For continuity, \(C = \frac{1}{4}\).
Question
Functions satisfy \(f'(x) = g(x)\) and \(g'(x) = f(x)\). The second derivative of \((f \cdot g)(x)\) is:
Solution
First derivative:
\[ (f \cdot g)' = f'g + fg' = g^{2} + f^{2} \]Second derivative:
\[ (f \cdot g)'' = 2gg' + 2ff' = 2gf + 2fg = 4fg \]Question
Find the average rate of change of \(f(x) = \sin x + x\) on \([0, \pi]\).
Solution
Average rate of change formula:
\[ \frac{f(\pi) - f(0)}{\pi - 0} = \frac{(\sin\pi + \pi) - (\sin 0 + 0)}{\pi} = \frac{\pi}{\pi} = 1 \]Question
Find the area of the shaded region between \(y = \sin x\) and \(y = \frac{1}{2}\) on \([0, \pi]\).

Solution
Intersection points: \(\sin x = \frac{1}{2} \Rightarrow x = \frac{\pi}{6}, \frac{5\pi}{6}\). Area:
\[ \begin{aligned} A &= \int_{0}^{\pi/6} \sin x \, dx + \int_{\pi/6}^{5\pi/6} \frac{1}{2} \, dx + \int_{5\pi/6}^{\pi} \sin x \, dx \\ &= [-\cos x]_{0}^{\pi/6} + \frac{1}{2}\left(\frac{5\pi}{6} - \frac{\pi}{6}\right) + [-\cos x]_{5\pi/6}^{\pi} \\ &= \left(-\frac{\sqrt{3}}{2} + 1\right) + \frac{\pi}{3} + \left(1 + \frac{\sqrt{3}}{2}\right) = 2 + \frac{\pi}{3} - \sqrt{3} \end{aligned} \]Question
Given \(g(x) = f(x^{2})\), \(f(x) = h(x^{3}+1)\), and \(h'(x) = 2x+1\), find \(g'(x)\).
Solution
Combine functions:
\[ g(x) = f(x^{2}) = h((x^{2})^{3} + 1) = h(x^{6} + 1) \]Apply chain rule:
\[ g'(x) = h'(x^{6}+1) \cdot 6x^{5} = [2(x^{6}+1) + 1] \cdot 6x^{5} = 12x^{11} + 18x^{5} \]