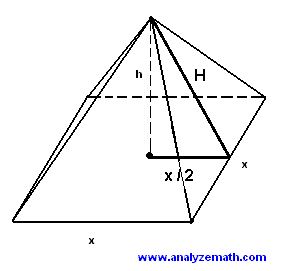
The first derivative is used to minimize the surface area of a pyramid with a square base.

Solution to Problem 1:
This problem has been solved graphically. Here we solve it more rigorously using the first derivative.
We first use the formula of the volume of a pyramid to write the equation:
\[ \frac{1}{3} h x^2 = 1000\]
The pyramid is made up of 4 triangles and a square (base)
The area of one triangle is given by
\( s = \dfrac{1}{2} H x \)
The slant height \( H \) is given by
\( H = \sqrt{h^2 + \left(\frac{x}{2}\right)^2} \)
The surface area \(S\) of the pyramid is given by the sum of the 4 areas of the 4 triangle and the area of the base \( x^2 \).
\(S = 4 (\dfrac{1}{2} H x) + x^2\)
\(= 2x \sqrt{h^2 + \left(\frac{x}{2}\right)^2} + x^2\)
Solve the equation \(\dfrac{1}{3} h x^2 = 1000\) for \(h\) to obtain:
\(h = \dfrac{3000}{x^2}\)
Substitute \(h\) in the surface area formula by \(\dfrac{3000}{x^2}\) to obtain a formula for \(S\) in terms of \(x\) (\(x\) positive) only and rewrite it as follows:
\( S = 2x \sqrt{\left(\dfrac{3000}{x^2}\right)^2 + \left(\frac{x}{2}\right)^2} + x^2 \)
Rewrite \( S \) as
\(S = \sqrt{(36 \times 10^6 + x^6)} \cdot \dfrac{1}{x} + x^2\)
\( \quad = \dfrac{\sqrt{36 \times 10^6 + x^6}}{x} + x^2\)
Let constant \(k = 36 \times 10^6\) and differentiate \(S\) with respect to \(x\).
\(\dfrac{dS}{dx} = \left[\dfrac{3x^6(k + x^6)^{-1/2} - (k + x^6)^{1/2}}{x^2}\right] + 2x\)
Multiply numerator and denominator by \((k + x^6)^{1/2}\) and simplify.
\(\dfrac{dS}{dx} = \dfrac{2x^6 - k}{x^2(k + x^6)^{1/2}} + 2x\)
A graph of \(\dfrac{dS}{dx}\) is shown below. For \(x > 0\), \(\dfrac{dS}{dx}\) has a zero and is negative to the left of that zero and positive to the right of the zero. This means that \(S\) has a minimum value that may be located by setting \(\dfrac{dS}{dx} = 0\) and solve for \(x\).

