Limits of Absolute Value Functions Questions

How to find the limits of absolute value functions; several examples and detailed solutions are presented along with graphical interpretations. A set of exercises with answers is presented at the bottom of the page.

Find the limits of the following functions.

Question

Find the limit: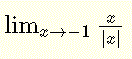
Solution
The steps to find the limit are:

Question

Evaluate the limit:
Solution
The steps to find the limit are

\( \)\( \)\( \)

Question

Find the limit: \( \lim_{x \to 0} \frac{x}{|x|} \)
Solution
\( \lim_{x \to 0} \frac{x}{|x|} = \frac{0}{|0|} \; \; \text{indeterminate form} \)
Recall that
\( | x | = x \) for \( x \le 0 \) and \( | x | = - x \) for \( x \lt 0 \)
Let us calculate the limit from the left of \( x = 0 \) where \( x \lt 0 \) and therefore \( | x | = - x \)
\( \lim_{x \to 0^-} \frac{x}{|x|} = \lim_{x \to 0^-} \frac{x}{- x} = \lim_{x \to 0^-} - 1 = -1 \)
Let us calculate the limit from the right of \( x = 0 \) where \( x \gt 0 \) and therefore \( | x | = x \)
\( \lim_{x \to 0^+} \frac{x}{|x|} = \lim_{x \to 0^+} \frac{x}{x} = \lim_{x \to 0^+} 1 =1 \)
The limits from the left and from the right of x = 0 are not equal, therefore
\( \lim_{x \to 0} \frac{x}{|x|} \; \; \text{does not exist} \)
The graph of f(x) = x / |x| is shown below and we clearly see that the limits from the left and right of 0 are not equal.

Question

Evaluate the limit: \( \lim_{x \to \infty} \frac{x}{|x|} \)
Solution
as x increases indefinitely , x > 0 and therefore |x| = x
Hence
\( \lim_{x \to \infty} \frac{x}{|x|} = \lim_{x \to \infty} \frac{x}{x} = \lim_{x \to \infty} 1 = 1 \)

Question

Find the limit: \( \lim_{x \to -\infty} \frac{x}{|x|} \)
Solution
as x decreases indefinitely , x < 0 and therefore |x| = - x
Hence
\( \lim_{x \to -\infty} \frac{x}{|x|} = \lim_{x \to -\infty} \frac{x}{ - x} = \lim_{x \to \infty} - 1 = - 1 \)

Question

Does the limit \( \lim_{x \to - 2} \frac{|x + 2|}{x + 2} \) exists?
Solution
\( \lim_{x \to - 2} \frac{|x + 2|}{x + 2} = \lim_{x \to - 2} \frac{|- 2 + 2|}{- 2 + 2} = \dfrac{0}{0} \;\; \text{indeterminate} \)
Let us calculate the limit from the left of -2 where x ≤ - 2 and from the right of -2 where x ≥ - 2 separateley.
Recall that
If x + 2 ≥ 0 or x ≥ - 2 then | x + 2 | = x + 2
and
If x + 2 ≤ 0 or x ≤ - 2 then | x + 2 | = - \( ( x + 2 ) \)
Let us calculate the limit from the left of x = - 2.
\( \lim_{x \to - 2^-} \frac{|x + 2|}{x + 2} = \lim_{x \to -2^-} \frac{-(x + 2)}{x + 2} = \lim_{x \to -2^-} - 1 = -1 \)
Let us calculate the limit from the right of x = - 2
\( \lim_{x \to - 2^+} \frac{|x + 2|}{x + 2} = \lim_{x \to - 2^+} \frac{x + 2}{x + 2} = \lim_{x \to -2^+} 1 = 1 \)
The limits from the left and from the right of x = - 2 are not equal, therefore
\( \lim_{x \to - 2} \frac{|x + 2|}{x + 2} \; \; \text{does not exist} \)

Question

Find the limit: \( \lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} \)
Solution
\( \lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} = \frac{(1)^2+2(1)-3}{|(1) - 1|} = \dfrac{0}{0} \; \; \text{indeterminate} \)
At x = 1 both numerator and denominator are equal to zero, they therefore have a common factor x - 1. We factor the numerator.
\( \lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1} \frac{(x-1)(x+3)}{|x - 1|} \)
Recall that
| x - 1 | = x - 1 for x - 1 ≥ 0 or x ≥ 1
and
| x - 1 | = - \( ( x - 1 ) \) for x - 1 < 0 or x < 1
Let us calculate the limit from the left of x = 1
\( \lim_{x \to 1^-} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1^-} \frac{(x-1)(x+3)}{-(x-1)} = \lim_{x \to 1^-} - (x + 3) = - 4 \)
Let us calculate the limit from the right of x = 1
\( \lim_{x \to 1^+} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1^+} \frac{(x-1)(x+3)}{x-1} = \lim_{x \to 1^-} (x + 3) = 4 \)
The limits from the left and from the right are not equal, therefore
\( \lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} \; \; \text{does not exist} \)
The graph of f(x) = (x^2 + 2 x - 3)/|x - 1| is shown below and we clearly see that the limits from the left and right of 1 are not equal.

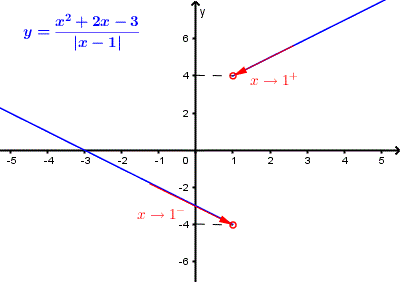
Question

Evaluate the limit: \( \lim_{x \to \infty} \frac{x^2+5x+7}{|x + 2|} \)
Solution
As x increases indefinitely, x + 2 also increases indefinitely and therefore x + 2 > 0, hence
\( \lim_{x \to \infty} \frac{x^2+5x+7}{|x + 2|} = \lim_{x \to \infty} \frac{x^2+5x+7}{x + 2} = + \infty \)

Question

Find the limit: \( \lim_{x \to - \infty} \frac{x^2+5x+7}{|x + 2|} \)
Solution
As x decreases indefinitely, x + 2 also decreases indefinitely and therefore x + 2 < 0, hence
\( \lim_{x \to -\infty} \frac{x^2+5x+7}{|x + 2|} = \lim_{x \to -\infty} \frac{x^2+5x+7}{-(x + 2)} = + \infty \)
The graph of \( f(x) = (x^2 + 5 x + 7)/|x + 2| \) is shown below and we clearly see that \( y = f(x) \) increases indefinitely as x increases indefinitely and also as x decreases indefinitely.

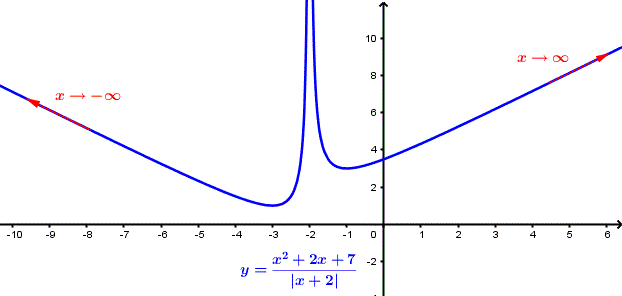
Exercises

Find the limits
1) \( \lim_{x \to 0} \frac{x^2}{|x|} \)
2) \( \lim_{x \to - 6^-} \frac{-(x + 6)}{|x + 6|} \)
3) \( \lim_{x \to - 6^+} \frac{-(x + 6)}{|x + 6|} \)
4) \( \lim_{x \to 3} \frac{x^2-x-6}{|x - 3|} \)

Answers to Above Exercises

1) 0
2) 1
3) - 1
4) does not exist

More References and links

Calculus Tutorials and Problems - Limits
Find Limits of Functions in Calculus
Introduction to Limits in Calculus
Properties of Limits of Mathematical Functions in Calculus
limits of basic functions
Questions and Answers on Limits in Calculus