Définition et équation d'une ellipse à axe vertical
Une ellipse est l'ensemble de tous les points \( M(x,y)\) dans un plan tel que la somme des distances de \( M \) aux points fixes \( F_1 \) et \( F_2 \) appelée le foyers (pluriel de focus) est égal à une constante.
\( \overline{MF_1} + \overline{MF_2} = \sqrt{(x+c)^2+y^2} + \sqrt{(x-c)^2+y^2} = 2 a \)
Pour \( a \ge b \ge 0 \), en éliminant les racines carrées par mise au carré et en simplifiant à l'aide de la relation \( a^2 = b^2 + c^2\), on peut se retrouver avec l'équation standard d'un ellispe donnée par :
\( \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \)
La largeur de l'ellipse est \( 2 a \) et la hauteur est \( 2 b \)
Le point \(O(0,0)\) est le centre de l'ellipse.
Les points \( V_1(a,0) \) et \( V_2(-a,0) \) sont appelés les sommets de l'ellipse.
Les foyers sont à \( F_1(c,0) \) et \( F_2(-c,0) \)
Exemple 1
Une ellipse centrée en \( (0,0) \) a x intercepte en \( (7,0) \) et \( ( -7 ,0) \) et y intercepte en \( (0,4) \) et \( ( 0,-4) \). Trouver l'équation de l'ellipse et les foyers \( F_1 \) et \( F_2 \)
Solution de l'exemple 1
L'équation d'une ellipse dont le centre est à l'origine est donnée par
\( \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \) , \( a \gt 0 \) et \( b \gt 0 \)
Trouvez l'axe des x en définissant y = 0 dans l'équation ci-dessus
\( \dfrac{x^2}{a^2} + \dfrac{0^2}{b^2} = 1 \)
Simplifier
\( \dfrac{x^2}{a^2} = 1 \)
Résoudre pour \( x \)
\( x = a \) et \( x = - a \)
Les interceptions x sont données par \( (7,0) \) et \( ( -7 ,0) \) ce qui donne \( a = 7 \).
Trouvez l'axe y en définissant x = 0 dans l'équation générale donnée ci-dessus
\( \dfrac{0^2}{a^2} + \dfrac{y^2}{b^2} = 1 \)
Simplifier
\( \dfrac{y^2}{b^2} = 1 \)
Résoudre pour \( y \)
\( y = b \) et \( y = - b \)
Les ordonnées à l'origine sont données par \( (0,4) \) et \( ( 0 , -4) \) ce qui donne \( b = 4 \).
Afin de trouver les foyers, nous devons d'abord trouver le paramètre \( c \) qui est lié à \( a \) et \( b \) par
\( a^2 = b^2 + c^2\)
Remplacez \( a \) et \( b \) par leurs valeurs et résolvez pour \(c \)
\( 7^2 = 4^2 + c^2\)
\(c = \sqrt{49 - 16} = \sqrt{33} \)
Les coordonnées des deux foyers F1 et F2 sont données par
\( F_1(c,0) = F_1(\sqrt{33} , 0) \) et \( F_1( - c,0) = F_1( - \sqrt{33} , 0) \)
Équation générale d'une ellipse
On peut généraliser et écrire l'équation d'une ellipse dont le centre est en \( O(h,k) \) comme suit
avec des foyers en \( F_1(c+h,k) \) et \( F_2(-c+h,k) \) et des sommets en \( V_1(a+h,k) \) et \( V_2(- a+h,k)\).
Exemple 2
Trouvez le centre, les foyers et les sommets de l'ellipse donnée par l'équation \( (x - 1)^2 + 4(y-2)^2 = 16 \) puis utilisez une calculatrice graphique pour représenter graphiquement l'équation donnée et vérifiez vos réponses. .
Solution de l'exemple 2
Réécrivez l'équation donnée sous forme standard en divisant tous les termes par 16.
\( \dfrac{(x - 1)^2}{16} + \dfrac{4(y-2)^2}{16} = \dfrac{16}{16} \) .
Simplifiez et écrivez les dénominateurs des termes de gauche sous forme de carrés
\( \dfrac{(x - 1)^2}{4^2} + \dfrac{(y-2)^2}{2^2} = 1 \)
Comparez l'équation ci-dessus d'une ellipse en standard pour à l'équation générale \( \dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1 \) et identifier les paramètres \( a, b, h\) et \( k \).
\(a = 4, b = 2, h = 1\) et \( k = 2 \)
Le centre est au point \( O(h,k) = O(1,2) \)
Trouvez le paramètre \( c \) en utilisant la relation \( a^2 = b^2 + c^2\)
\(c = \sqrt{a^2 - b^2} = \sqrt{16 - 4} = 2 \sqrt{3} \)
Les foyers sont aux points
\( F_1(c+h,k) = F_1(2 \sqrt{3}+1,2) \) et \( F_2(-c+h,k) = F_2(-2 \sqrt{3}+1 ,2) \)
Les sommets sont aux points
\( V_1(a+h,k) = V_1(5,2) \) et \( V_2(-a+h,k) = V_2(-3,2) \)
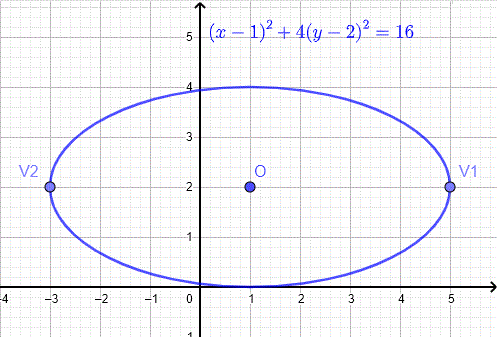
Le graphique de l'équation donnée \( (x - 1)^2 + 4(y-2)^2 = 16 \) est présenté ci-dessous et c'est celui d'une ellipse de centre en \(O(1,2)\ ) et les sommets à \(V_1(5,2) \) et \(V_2(-3,2) \) comme calculé ci-dessus.
Turorial interactif sur l'équation d'une ellipse
Une application pour explorer l'équation d'une parabole et ses propriétés est maintenant présentée. L'équation utilisée est l'équation standard qui a la forme
L'exploration s'effectue en modifiant les paramètres \( a, b, h \) et \( k \) inclus dans l'équation ci-dessus. Les valeurs par défaut, lorsque vous ouvrez cette page, sont : \( a = 4, b = 2, h = 2 \) et \( k = 3 \).
Certaines activités sont répertoriées ci-dessous mais de nombreuses autres activités peuvent être générées.
Cliquez sur le bouton "Plot Equation" pour commencer.
Passez le curseur de la souris sur le graphique du point tracé pour lire les coordonnées.
Cliquez sur le bouton au-dessus de « Tracer l'équation ». Vous pouvez passer le curseur mousse sur le graphique de l'ellipse et des points pour lire les coordonnées. Vous pouvez également passer le curseur mousse en haut à droite du graphique pour avoir les options de zoom, de téléchargement du graphique sous forme de fichier png, ...
1 - Sélectionnez un point M sur le graphique de l'ellipse, passez la mousse dessus et lisez les coordonnées. Lire les coordonnées de F1 et F2 (légende de droite) ou survoler la mousse et lire les coordonnées et montrer que la somme des distances \( \overline{MF_1} + \overline{MF_2} \) est proche de \( 2a\) .
Vous pouvez réaliser l’activité ci-dessus pour différentes valeurs de \( a, b, h\) et \( k \) et autant de points que nécessaire pour mieux comprendre la définition d’une ellipse.
2 - Utilisez les valeurs de \( a \) et \( b \) pour trouver \( c \) en utilisant la relation entre \( a, b\) et \( c \) donnée par \( a^2 = b ^2 + c^2\).
Utilisez les résultats ci-dessus pour trouver les coordonnées de \( F_1, F_2, V_1 \) et \( V_2 \) et vérifiez les résultats graphiquement.
3 - Définissez \( a, b, h\) et \( k \) sur certaines valeurs. Recherchez les interceptions x et y et vérifiez vos résultats graphiquement.
4 - Exercice :
Montrer par des calculs algébriques que l'équation suivante \( \dfrac{(x + 2)^2}{5} + 5(y-3)^2 = 5 \) est celle d'une ellipse et trouver le centre, les foyers et les sommets de l'ellipse donnée par l'équation, puis utilisez l'application pour la représenter graphiquement et vérifier vos réponses.
Plus de références et de liens vers des sujets liés à l'équation de l'ellipse
