Gleichung eines Kreises
Seiteninhalt
Gleichung eines Kreises in Standardform
Unten ist ein Kreis dargestellt, dessen Mittelpunkt C durch seine Koordinaten C(h,k) gegeben ist. Per Definition haben alle Punkte M(x,y) auf dem Kreis den gleichen Abstand vom Mittelpunkt. Mit anderen Worten: Ein Kreis mit dem Mittelpunkt C ist die Menge aller Punkte, die den gleichen Abstand vom Punkt C haben. Dieser Abstand zwischen C und einem beliebigen Punkt auf dem Kreis wird als Radius bezeichnet und hat in der folgenden Grafik die Länge r .

Der Abstand vom Mittelpunkt C(h,k) zu einem Punkt M(x,y) auf dem Kreis ist gegeben durch
 Um die Gleichung zu finden, verwenden wir die Definition, um zu schreiben, dass der Abstand CM gleich dem Radius r ist
Um die Gleichung zu finden, verwenden wir die Definition, um zu schreiben, dass der Abstand CM gleich dem Radius r ist
 Das Arbeiten mit der Quadratwurzel bringt zusätzliche Schwierigkeiten mit sich, die vermieden werden können. Die Quadratwurzel in der obigen Gleichung kann durch Quadrieren beider Seiten der Gleichung eliminiert werden.
Das Arbeiten mit der Quadratwurzel bringt zusätzliche Schwierigkeiten mit sich, die vermieden werden können. Die Quadratwurzel in der obigen Gleichung kann durch Quadrieren beider Seiten der Gleichung eliminiert werden.
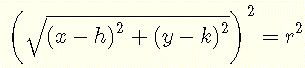 Vereinfachen Sie, um die Standardgleichung eines Kreises mit Mittelpunkt C(h,k) und Radius r
Vereinfachen Sie, um die Standardgleichung eines Kreises mit Mittelpunkt C(h,k) und Radius r
\( \) \( \) \( \) \( \)
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Beispiele
Beispiel 1
Finden Sie die Standardgleichung des Kreises mit Mittelpunkt C(2,5) und Radius r = 2
Lösung zu Beispiel 1
Bei gegebenem Mittelpunkt und Radius lautet die Standardgleichung des Kreises wie folgt:
\( (x - 2)^2 + (y - 5)^2 = 2^2 \)
Punkte auf, innerhalb oder außerhalb eines Kreises
Um herauszufinden, ob ein gegebener Punkt auf einem Kreis, innerhalb eines Kreises oder außerhalb eines Kreises liegt, vergleichen wir das Quadrat des Abstands vom Mittelpunkt des Kreises zum gegebenen Punkt mit dem Quadrat des Radius. Wir verwenden das Quadrat des Abstands anstelle des Abstands, um die Verwendung der Quadratwurzel zu vermeiden.
Für einen Kreis mit Mittelpunkt \( C(h,k) \) und Radius \( r \), Punkt \( P \) mit Koordinaten \( (x_0 , y_0) \)
1) liegt auf dem Kreis, wenn folgende Gleichung erfüllt ist:
\[ (x_0 - h)^2 + (y_0 - k)^2 = r^2 \]
2) liegt innerhalb des Kreises, wenn die folgende Ungleichung erfüllt ist:
\[ (x_0 - h)^2 + (y_0 - k)^2 \lt r^2 \]
3) liegt außerhalb des Kreises, wenn die folgende Ungleichung erfüllt ist:
\[ (x_0 - h)^2 + (y_0 - k)^2 \gt r^2 \]
Beispiel 2
Gleichung eines Kreises und Punkten innerhalb, außerhalb oder auf dem Kreis
Welcher der folgenden Punkte \( P_1(1,5) \) , \( P_2(2,3) \) und \( P_3(4,7) \) liegt innerhalb, außerhalb oder auf dem Kreis aus Beispiel 1?
Lösung zu Beispiel 2
Der Mittelpunkt des Kreises in Beispiel 1 liegt bei \( C(2,5) \) und hat den Radius \( r = 2 \)
Ermitteln Sie das Quadrat des Abstands vom Mittelpunkt des Kreises zu jedem der angegebenen Punkte und vergleichen Sie es mit dem Quadrat des Radius
Das Quadrat des Abstands von \( C \) zu \( P_1 \) ist gegeben durch: \( (2-1)^2 + (5-5)^2 = 1\), was kleiner ist als \( r^2 = 4\). Daher liegt der Punkt \( P_1 \) innerhalb des Kreises.
Das Quadrat des Abstands von \( C \) zu \( P_2 \) ist gegeben durch: \( (2-2)^2 + (5-3)^2 = 4\), was gleich \( r^2 = 4\). Daher liegt der Punkt \( P_1 \) auf dem Kreis.
Das Quadrat des Abstands von \( C \) zu \( P_3 \) ist gegeben durch: \( (2-4)^2 + (5-7)^2 = 8\), das größer ist als \( r^2 = 4\). Daher liegt der Punkt \( P_3 \) außerhalb des Kreises.
Der Kreis und die drei Punkte sind unten dargestellt und wir können die oben gefundene Antwort leicht überprüfen.

Tangente an einen Kreis
Eine der wichtigen Eigenschaften einer Tangente an einen Kreis besteht darin, dass sie senkrecht zur Linie durch den Mittelpunkt \( C \) und den Tangentialpunkt \( M \) verläuft, wie unten gezeigt.

Beispiel 3 Gleichung eines Kreises und Punkten innerhalb, außerhalb oder auf dem Kreis
Finden Sie die Gleichung der Tangente an den Kreis mit der Gleichung \( (x + 2)^2 + (y - 2)^2 = 5 \) am Punkt \( M(-4 , 3) \).
Lösung zu Beispiel 3
Wenn wir die angegebene Gleichung mit der oben angegebenen allgemeinen Standardgleichung vergleichen, schließen wir, dass der Mittelpunkt bei \( C(-2,2) \) liegt.
Die Steigung \( m_1 \) der Geraden durch \( C M \) ist gegeben durch
\( m_1 = \dfrac{3-2}{-4-(-2)} = -\dfrac{1}{2} \)
Sei \( m_2 \) die Steigung der Tangente. Da die Tangente und \( C M \) senkrecht zueinander stehen, hängen die Steigungen \( m_1 \) und \( m_2 \) zusammen
\( m_1 \times m_2 = -1 \)
was gibt
\( (-\dfrac{1}{2}) \times m_2 = -1 \)
Lösen Sie nach \( m_2 \) auf, um zu erhalten
\( m_2 = 2 \)
Wir kennen jetzt die Steigung \( m_2 \) und \( M(-4,3) \) den Tangentenpunkt, durch den die Tangente verläuft. Wir verwenden die Punktsteigungsformel, um die Gleichung der Tangente an die gegebene Linie zu finden Kreis
\( y - 3 = 2 (x - (-4)) \)
\( y = 2 x + 11 \)
Zeichnen Sie als Übung den gegebenen Kreis und die Gleichung der oben gefundenen Tangente auf und überprüfen Sie grafisch, ob sie den Punkt (-4,3) tangieren.
Allgemeine Form der Kreisgleichung
Beginnen wir mit der Standardgleichung eines Kreises
\( (x - h)^2 + (y - k)^2 = r^2 \)
Expandieren
\( x^2 - 2 h x + h^2 + y^2 - 2 k y + k^2 = r^2 \)
Lassen
\( A = - 2 h\), \( B = - 2 k \) und \( C = h^2 + k^2 - r^2\)
Setzen Sie die erweiterte Gleichung ein, um die allgemeine Form der Kreisgleichung zu erhalten.
\( x^2 + y^2 + A x + B y + C = 0 \)
Beispiel 4 Finden Sie die Gleichung eines Kreises mit drei Punkten
Finden Sie die Kreisgleichung durch die Punkte \( P_1(6,4) \), \( P_2(-1,5) \) und \( P_3(2,-4) \).
Lösung zu Beispiel 4
Die Koordinaten eines Punktes auf einem Kreis müssen die Kreisgleichung erfüllen. Wir schreiben, dass die Koordinaten jedes der gegebenen Punkte die Kreisgleichung in der allgemeinen Form erfüllen: \( x^2 + y^2 + A x + B y + C = 0 \).
Punkt \( P_1(6,4) \) liegt auf dem Kreis; Ersetzen Sie \( x \) durch \( 6 \) und \( y \) durch \( 4 \) in der Gleichung, daher: \( 6^2 + 4^2 + 6 A + 4 B + C = 0 \)
Punkt \( P_2(-1,5) \) liegt auf dem Kreis; Ersetzen Sie \( x \) durch \( -1 \) und \( y \) durch \( 5 \) in der Gleichung, also: \( (-1)^2 + 5^2 - A + 5 B + C = 0 \)
Punkt \( P_3(2,-4) \) liegt auf dem Kreis; Ersetzen Sie \( x \) durch \( 2 \) und \( y \) durch \( -4 \) in der Gleichung, also: \( 2^2 + (-4)^2 + 2 A - 4 B + C = 0 \)
Lösen Sie für (A,B,C) das oben erhaltene und unten in Standardform gezeigte Gleichungssystem
\( \begin{cases} 6 A + 4 B + C = -52\\ - A + 5 B + C = - 26 \\ 2 A - 4 B + C = -20 \end{cases} \)
Verwenden Sie eine beliebige Methode, um die Lösung zu erhalten
\( A = -4\) , \( B = -2 \), \( C = -20 \)
Wir ersetzen nun \( A \), \( B \) und \( C \) durch ihre Werte und schreiben die Kreisgleichung wie folgt:
\( x^2 + y^2 - 4 x - 2 y - 20 = 0 \)
Der oben gefundene Kreis und die drei Punkte sind in der Grafik unten dargestellt.

Beispiel 5 Schreiben Sie die allgemeine Kreisgleichung in die Standardform um.
Schreiben Sie die Gleichung des durch \( x^2 + y^2 + 6x - 2y + 5 = 0 \) gegebenen Kreises neu und ermitteln Sie dessen Mittelpunkt und Radius.
Lösung zu Beispiel 5
Setzen Sie in Klammern die Terme in \( x\) und \( x^2 \) zusammen und die Terme in \( y \) und \( y^2\) zusammen
\( (x^2 + 6x) + (y^2 - 2y) + 5 = 0 \)
Vervollständigen Sie das Quadrat jedes Binomials innerhalb der Parehthesen
\( (x^2 + 3)^2 - 3^2 + (y^2 - 1)^2 - (-1)^2 + 5 = 0 \)
Schreiben Sie in Standardform
\( (x + 3)^2 + (y - 1)^2 = 5 \)
Vergleichen Sie die obige Gleichung mit der Standardgleichung \( (x - h)^2 + (y - k)^2 = r^2\) und identifizieren Sie die Koordinaten \( h \) und \( k \) des Mittelpunkts von der Kreis und der Radius \( r \).
\( h = - 3\) , \( k = 1\) und \( r^2 = 5 \)
Der Mittelpunkt des Kreises hat die Koordinaten \( (-3 , 1) \) und den Radius \( r = \sqrt 5 \)
Weitere Tutorials zur Kreisgleichung finden Sie auf dieser Website.
Interaktive Tutorials zum Erkunden der Kreisgleichung
Die Untersuchung erfolgt durch Ändern der Parameter h, k und r, die in der Standardgleichung \( (x - h)^2 + (y - k)^2 = r^2\) enthalten sind.
Dies ist eine HTML5-App, die dabei hilft, die Gleichung eines Kreises und die Eigenschaften des Kreises zu erkunden.
1 - Klicken Sie zum Starten auf die Schaltfläche oben „Zeichnen“. Verwenden Sie die Schaltflächen + und - im linken Bereich, um hinein- und herauszuzoomen.
2 - Verwenden Sie die Schieberegler und/oder Eingabefelder, um die Parameter h und k auf Null und den Parameter r auf 1 zu setzen. Überprüfen Sie, ob der Mittelpunkt des angezeigten Kreises bei (0,0) liegt und der Radius gleich 1 ist.
3 – Sonderfall: Verwenden Sie die Schieberegler und/oder Eingabefelder, um r auf Null und die Parameter h und k auf unterschiedliche Werte zu setzen. Der Graph des Kreises ist ein Punkt, erklären Sie.
(Hinweis: Lösen Sie die Gleichung \( (x - h)^2 + (y - k)^2 = 0^2\))
4 – Halten Sie r gleich 1 und verschieben Sie den Kreis, indem Sie h und k ändern. Überprüfen Sie, ob der Mittelpunkt des Kreises bei (h, k) liegt.
5 - Halten Sie h und k konstant und ändern Sie r. Überprüfen Sie, ob der Kreis den Radius r hat.
6 - Setzen Sie h, k und r auf 1. Der Kreis hat einen Schnittpunkt mit der x-Achse und einen Schnittpunkt mit der y-Achse. Diese werden als x- und y-Achsenabschnitte bezeichnet. Finden Sie diese Punkte analytisch mithilfe der Kreisgleichung.
\[ (x - h)^2 + (y - k)^2 = r^2\]
(Hinweis: Um die $x$-Achsenabschnitte zu finden, setzen Sie y = 0 in der Gleichung und lösen Sie nach x auf. Um die y-Achsenabschnitte zu finden, setzen Sie x = 0 in der Gleichung und lösen Sie nach y auf.)
7- Setzen Sie r auf 2 und h auf einen bestimmten Wert. Ändere k von -1,8 auf 1,8 (|h| < r). Wie viele x-Achsenabschnitte gibt es? Setzen Sie k auf 2 (den Radius). Wie viele x-Achsenabschnitte gibt es? Setzen Sie k auf -2. Wie viele x-Achsenabschnitte gibt es? Stellen Sie k auf Werte größer als 2 (den Radius) ein. Wie viele x-Achsenabschnitte gibt es? Setzen Sie k auf Werte kleiner als -2. Wie viele x-Achsenabschnitte gibt es? Erklären Sie analytisch.
8- Versuchen Sie die gleiche Untersuchung wie in 7 oben mit den y-Achsenabschnitten, indem Sie den Wert von h ändern.
9- Übung: Finden Sie (analytisch) Werte von h, k und r, so dass der mit diesen Werten verbundene Kreis keine x- oder y-Achsenabschnitte hat. Überprüfen Sie Ihre Antwort grafisch.
Referenzen und Links
Schritt-für-Schritt-Löser für Mathe-Arbeitsblätter
X- und y-Achsenabschnitte von Kreisen finden – Rechner
Tutorial zur Kreisgleichung
Matheaufgaben und Online-Selbsttests.
Homepage

 Um die Gleichung zu finden, verwenden wir die Definition, um zu schreiben, dass der Abstand CM gleich dem Radius r ist
Um die Gleichung zu finden, verwenden wir die Definition, um zu schreiben, dass der Abstand CM gleich dem Radius r ist
 Das Arbeiten mit der Quadratwurzel bringt zusätzliche Schwierigkeiten mit sich, die vermieden werden können. Die Quadratwurzel in der obigen Gleichung kann durch Quadrieren beider Seiten der Gleichung eliminiert werden.
Das Arbeiten mit der Quadratwurzel bringt zusätzliche Schwierigkeiten mit sich, die vermieden werden können. Die Quadratwurzel in der obigen Gleichung kann durch Quadrieren beider Seiten der Gleichung eliminiert werden.
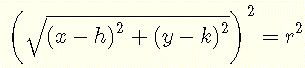 Vereinfachen Sie, um die Standardgleichung eines Kreises mit Mittelpunkt C(h,k) und Radius r
Vereinfachen Sie, um die Standardgleichung eines Kreises mit Mittelpunkt C(h,k) und Radius r


