The Use of Graphing Software in the Mathematics Classroom (2)

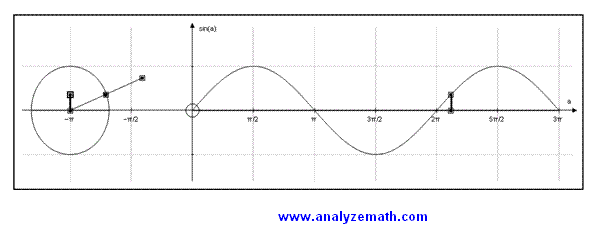
2. AUTOGRAPH SOFTWARE

Autograph software has 2D and 3D graphing capabilities for pre-calculus topics such as graphing, transformations, inverse functions, trigonometric functions, conic sections, vector, slope, calculus topics such as functions and integrals and topics in statistics. Autograph is very strong in visualizing mathematical concepts. More strength of this software lie in the fact that parameters may be included in mathematical equations and functions and varied to see their effects on the graphs and hence gain a deep understanding of the properties of these mathematical objects. For example the parameters a, h and k included in the quadratic function f given by [13]

f(x)= a(x - h)2 + k

may be varied one at the time and changes in the graph explored. Such an experiment could be used to explore the coordinates of the vertex of the graph of function f and its range.

3. EXAMPLES OF STUDENTS CENTERED ACTIVITIES USING AUTOGRAPH

I will now present examples of activities where Autograph can be used as a tool to enhance understanding of topics in mathematics.

3.1 Explore the Definition and Graph of the Sine Function

Task: Students explore the relationship between the sine function as defined in the unit circle and its graph in rectangular systems of axis. This allows students to view the sine function using two representations that complement each other.

Sine function in unit circle and rectangular system of axes

Fig. 1: Sine function in unit circle and rectangular system of axes.

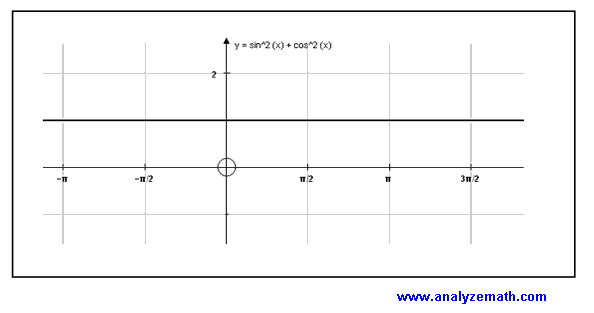
In trigonometry, the angle is defined as a measure of rotation and Autograph is a dynamic graphing software that can easily be used to explain of concept of angles and the relationship between the angle in standard position and the trigonometric functions associated with it. This activity allows students to explore the period, the range and the five key points over one period of the sine function.

3.2 Explore Identities

Task: Students explore the graphs of the two sides of equations and use the definition to decide whether a given equation is a conditional equation or an identity. Here are some example that I used in my classes.

  • 2x = 4
  • (x + 2)2 = x2 + 4x + 4
  • -2x2 + 3 = x
  • sin(x + pi/3) = sin(x) + sin(pi/3)
  • sin2(x) + cos2(x) = 1
  • cot(x) (sec(x) + tan(x)) = 1/sin(x) + 1

Verifying identities.

Fig. 2: Verifying identities.

This activity allows students to explore graphically the difference between a conditional equation and an identity. Questions on the definition of an identity put to the students before and after this activity showed that the students gained a deeper understanding of the concept of identities through this activity.

1, 2, 3, 4, 5,

SEARCH THIS SITE

Custom Search