Applications and Use of the Inverse Functions

Examples on how to apply and use inverse functions in real-life situations and to solve problems in mathematics.

Example 1

Use inverse functions to solve equations.

Solve the following equation:

\[ \log(x - 3) = 2 \]

Solution to Example 1

Since logarithmic and exponential functions are inverses of each other, we can write: \[ A = \log(B) \quad \text{if and only if} \quad B = 10^A \]
Using this property, rewrite the given equation: \[ x - 3 = 10^2 \]
Solve for \(x\): \[ x = 103 \]

Example 2

Use inverse functions to find the range of a function.

Find the range of the function \(f\) given by:

\[ f(x) = \frac{2x}{x - 3} \]

Solution to Example 2

The range of a one-to-one function is the domain of its inverse. First, we show that \(f\) is one-to-one. Start with: \[ f(a) = f(b) \]
\[ \frac{2a}{a - 3} = \frac{2b}{b - 3} \]
Multiply both sides by \((a-3)(b-3)\): \[ 2a(b - 3) = 2b(a - 3) \]
Expand both sides: \[ 2ab - 6a = 2ab - 6b \]
Simplify to obtain: \[ a = b \]
Hence, the function is one-to-one. Now find its inverse.
\[ y = \frac{2x}{x - 3} \]
Interchange \(x\) and \(y\) and solve for \(y\): \[ x = \frac{2y}{y - 3} \] \[ y = \frac{3x}{2 - x} \]
Therefore: \[ f^{-1}(x) = \frac{3x}{2 - x} \]
The domain of \(f^{-1}\) excludes \(x = 2\). Hence, the range of \(f\) is all real numbers except 2.

Example 3

Use inverse functions to find the angle of elevation.

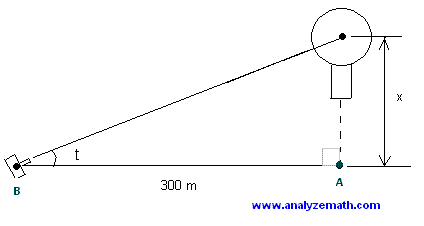
A camera photographs a hot-air balloon rising vertically. The camera is 300 meters from the launch point. The angle of elevation \(t\) depends on the height \(x\) of the balloon.

(a) Find \(t\) as a function of \(x\).
(b) Find \(t\) when \(x = 150, 300, 600\) meters.
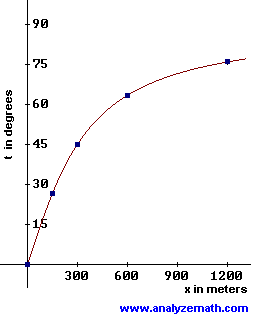
(c) Graph \(t\) as a function of \(x\).

Solution to Example 3

Using right-triangle trigonometry: \[ \tan(t) = \frac{x}{300} \]
Apply the inverse tangent: \[ t = \tan^{-1}\left(\frac{x}{300}\right) \]
Values of \(t\):
\[ t(150) = 25.6^\circ, \quad t(300) = 45.0^\circ, \quad t(600) = 63.4^\circ \]
Graph \(t\) using the following table:

x	t (degrees)
0	0
150	25.6
300	45.0
600	63.4
1200	76.0
3000	84.3

Example 4

Use inverse functions to find the radius of a right circular cone.

Five cones of height \(h = 50\) cm have volumes 200, 400, 800, 1600, and 3200 cm\(^3\). Find the radius of each cone.

Solution to Example 4

Volume formula: \[ V = \frac{1}{3}\pi r^2 h \]
Solve for \(r\): \[ r = \sqrt{\frac{3V}{\pi h}} \]
Computed radii:

\[ \begin{aligned} V = 200 &\Rightarrow r = 1.95\text{ cm} \\ V = 400 &\Rightarrow r = 2.76\text{ cm} \\ V = 800 &\Rightarrow r = 3.91\text{ cm} \\ V = 1600 &\Rightarrow r = 5.53\text{ cm} \\ V = 3200 &\Rightarrow r = 7.82\text{ cm} \end{aligned} \]

Example 5

Use inverse functions to solve population growth problems.

\[ P = 200{,}000 e^{0.01t} \]

Find when the population reaches 300,000; 400,000; and 500,000.

Solution to Example 5

Solve for \(t\): \[ t = \frac{\ln(P/200{,}000)}{0.01} \]