Linear Programming and Optimization

What is linear programming?
A two-variable linear programming has a linear function f(x,y) in two variables, called objective function, along with systems of linear inequalities called constraints which defines the feasible solution set as defined in systems of inequalities with two variables.
Linear programming is one of the methods of optimization where there is a need to find values of some variables x, y so that function f of the variables x, y has a maximum or minimum value depending on the application to solve. Possible applications of linear programming may be found in engineering, agriculture, medicine, finance, economics, etc.

The solutions to a linear programming problem may be solved using the following theorems:
Theorem 1
The solution of a linear programming problem, it it exists, must occur at a vertex of the feasible set associated with the constraints of the problem. If the solution associated with the constraints and the objective function occur at two adjacent vertices, then all points on the line segment joining these two vertices are solutions.

Theorem 2
In a linear programming problem with a feasible set A and objective function f(x,y) = a x + b y, the following cases may occur
1) If A is bounded, then f(x,y) has both a maximum and a minimum at the vertices of A.
2) If x ? 0 and y ? 0 and if A in unbounded, and both a and b are positive, then f(x,y) has a minimum at one (or more) of the vertices of A.

Examples with detailed solutions and explanations are presented.

Example 1: Find maximum value

Find the values of x and y that make z(x , y) = 2 x + 4 y maximum subject to the conditions shown below and find the value of z at these values of x and y
\[ \begin{cases} \ x \ge 0 \\ \ y \ge 0 \\ \ y \le x + 1 \\ \ 4y + x \le 10 \\ \ y - x \ge - 3 \\ \end{cases} \]

Solution to Example 1:
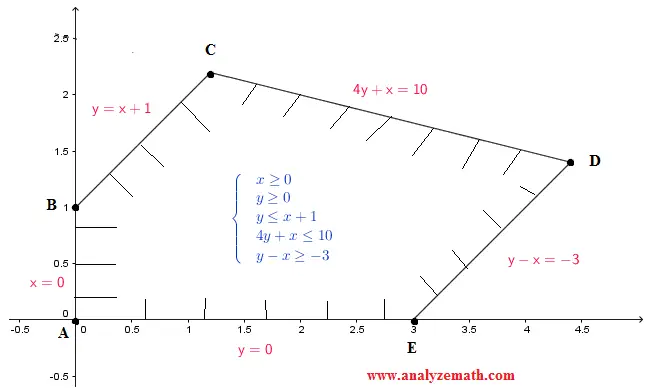
The solution set of the system of inequalities given above and the vertices of the feasible set obtained has already been found in Example 3 of "solving systems of inequalities in two variables". The solution set is shown in the figure below.

graphical solution to system of inequalities in example 1 .

The vertices were also found (in the same example) to be:
A(0 , 0), B(0 , 1), C(6/5 , 11/5), D(22/5 , 7/5), E( 3 , 0)
We now evaluate function z(x , y) = 2 x + 4 y at all 5 vertices of the feasible set.

at A: the x and y coordinates of A are x = 0 and y = 0.
Substitute x and y by 0 and 0 respectively in the linear function z = 2 x + 4 y to obtain z(A) = 2 (0) + 4 (0) = 0
at B: the x and y coordinates of B are x = 0 and y = 1.
Substitute x and y by 0 and 1 respectively in the linear function z = 2 x + 4 y to obtain z(B) = 2 (0) + 4 (1) = 4
at C: the x and y coordinates of C are x = 6/5 and y = 11/5.
Substitute x and y by 6/5 and 11/5 respectively in the linear function z = 2 x + 4 y to obtain z(B) = 2 (6/5) + 4 (11/5) = 11.2
at D: the x and y coordinates of D are x = 22/5 and y = 7/5.
Substitute x and y by 22/5 and 7/5 respectively in the linear function z = 2 x + 4 y to obtain z(B) = 2 (22/5) + 4 (7/5) = 14.4
at E: the x and y coordinates of D are x = 3 and y = 0.
Substitute x and y by 3 and 0 respectively in the linear function z = 2 x + 4 y to obtain z(B) = 2 (3) + 4 (0) = 6

The maximum value of z occur at vertex D with coordinates x = 22/5 and y = 7/5. Hence the solution of the given problem is Z has a maximum value at x = 22/5 and y = 7/5 and this value is 14.4

Example 2: Find minimum value

Find the minimum value of z(x , y) = 4 x + 7 y where x ? 0 and y ? 0 subject to the conditions
\[ \begin{cases} \ 2x + 3y \ge 6 \\ \ x - y/3 \le 4 \\ \ -2x+2y \le 8 \\ \ x + (5/2)y \le 13 \\ \end{cases} \]

Solution to Example 2:
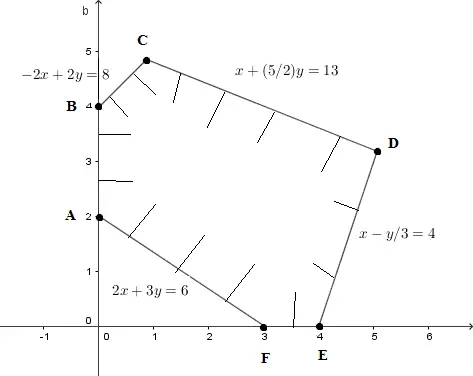
The feasible set to the systems of inequalities is shown below. A vertex is determined by solving the system of equations corresponding to the equations of the lines whose intersection is the vertex to be found.
Solve the system of equations 2x + 3y = 6 and x = 0 to find A(0 , 2)
Solve the system of equations x = 0 and -2x + 2y = 8 to find B(0 , 4)
Solve the system of equations -2x + 2y = 8 and x + (5/2)y = 13 to find C(6/7 , 34/7)
Solve the system of equations x + (5/2)y = 13 and x - y/3 = 4 to find D(86/17 , 54/17)
Solve the system of equations x - y/3 = 4 and y = 0 to find E(4 , 0)
Solve the system of equations y = 0 and 2x + 3y = 6 to find F(3 , 0)

graphical solution to system of inequalities in example 2 .

We now evaluate z(x , y) = 4 x + 7 y at each vertex found above
at A(0 , 2): z = 4(0) + 7(2) = 14
at B(0 , 4): z = 4(0) + 7(4) = 28
at C(6/7 , 34/7): z = 4(6/7) + 7(34/7) = 37.4
at D(86/17 , 54/17): z = 4(86/17) + 7(54/17) = 42.5
at E(4 , 0): z = 4(4) + 7(0) = 16
at F(3 , 0): z = 4(3) + 7(0) = 12
Function z = 4 x + 7y has a minimum value of 12 and occurs for x = 3 and y = 0 (vertex F).

Example 3: Many solutions

Find the maximum value of the function z = 3 x + 3 y where x ? 0 and y ? 0 subject to the conditions
\[ \begin{cases} \ x \le 6 \\ \ y \le 7 \\ \ y \le - x + 9 \\ \end{cases} \]

Solution to Example 3:

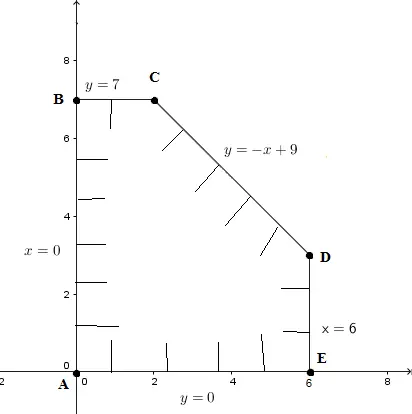
The feasible set to the systems of inequalities given above is shown below.
vertices are at (see examples 2 and 3 above on how to find them)
A(0 , 0)
B(0 , 7)
C(2 , 7)
D(6 , 3)
E(6 , 0)

graphical solution to system of inequalities in example 3 .

Evaluate function z = 3 x + 3 y at each vertex
at A(0 , 0) : z = 3 (0) + 3 (0) = 0
at B(0 , 7) : z = 3 (0) + 3 (7) = 21
at C(2 , 7) : z = 3 (2) + 3 (7) = 27
at D(6 , 3) : z = 3 (6) + 3 (3) = 27
at E(6 , 0) : z = 3 (6) + 3 (0) = 18
Function z = 3 x + 3 y has a maximum value at two vertices: C and D. In fact all points between C and D on the line y = - x + 9 gives z = 27.
Explanation: z may be written as
z = 3 (x + y)
The equation of the line through BC is y = - x + 9 may be written as x + y = 9
Substitute x + y by 9 in z = 3 (x + y) to obtain
z = 3 (9) = 27 and is maximum for all point on the line y = - x + 9.