Solve Systems of Inequalities with Two Variables

This is a tutorial on solving systems of inequalities with two variables. Examples with detailed explanations are presented.

In order to solve a system of inequalities, we first solve graphically each inequality in the given system on the same coordinate system and then find the region that is common to each solution (which is a region) of the inequality in the system: it is the intersection of all regions obtained and is called the feasible region.

Example 1: Solve graphically the system of inequalities

Solution to Example 1

We first use the methods developed in solving inequalities with two variables to solve each of the given inequalities in the system to solve.
Below is shown (in red) the solution set of the first inequality: \( x + 2y \ge - 2 \). Because the symbol of the inequality includes the equal sign, the graph of equation \( x + 2y = - 2 \) is a solid line.

.

We then solve the second inequality \( x + y \lt 0 \); it is shown below in blue. Because the symbol of the inequality does not include the equal sign, the graph of the equation \( x + y = 0 \) is a broken line.

.

We next find the region common region to the solution sets (the intersection of the two solution set) found above. The intersection is the set of points common to the two solution sets. Shown below with both red and blue hash lines.

.

Finally the solution set of the system of inequalities to solve is represented by the blue region. It is called the feasible region.

.

Example 2 Solve graphically the inequality and find the vertices of the region representing the solution set. \[ \begin{cases} \ x \gt y - 1 \\ \ 2x + y \le 2 \\ \ 4y \ge -3 x - 12 \\ \end{cases} \]

Solution to Example 2

We first solve the inequality \( x \gt y - 1 \). The solution set is the region with black hash lines.

.

We then solve the inequality \( 2x + y \le 2 \). The solution set is the region with red hash lines.

.

We next solve the inequality \( 4y \ge -3 x - 12 \). The solution set is the region with blue hash lines.

.

The solution set is the intersection of all three regions found above. It is shown below as a triangle.

.

Finally the solution set as a triangle also called the feasible region is shown below.

.

Now that we have the region representing the solution set which is a triangle, we are asked to find the coordinates of the vertices A, B and C which are points of intersection of the lines graphed to find the solution set of the system of inequalities.

Point A is the intersection of the lines through AB and AC
equation of line through AB: x = y - 1
equation of line through AC: 4y = - 3 x - 12
The point of intersection of AB and AC is the solution to the system of equations
\[ \begin{cases} \ x = y - 1 \\ \ 4y = -3 x - 12 \\ \end{cases} \]
Solve the above system to find y = - 9 / 7 and x = - 16 / 7.
Point A has the coordinates: A( - 16 / 7 , - 9 / 7)

Point B is the intersection of AB and BC and is found by solving the system of equation
\[ \begin{cases} \ x = y - 1 \\ \ 2x + y = 2 \\ \end{cases} \]
Solution: B(1 / 3 , 4 / 3)

Point C is the intersection of AC and BC and is found by solving the system of equation \[ \begin{cases} \ 4y = -3 x - 12 \\ \ 2x + y = 2 \\ \end{cases} \] Solution: C(4 , -6)

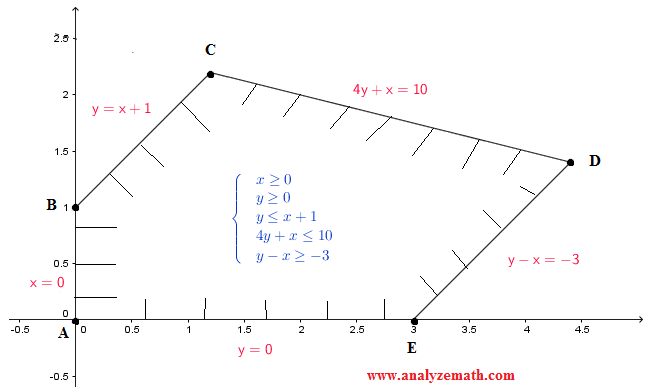
Example 3 Solve graphically the inequality and find the vertices of the region representing the solution set. \[ \begin{cases} \ x \ge 0 \\ \ y \ge 0 \\ \ y \le x + 1 \\ \ 4y + x \le 10 \\ \ y - x \ge - 3 \\ \end{cases} \]

Solution to Example 3

We first solve each inequality and then determine the common region which is the solution set to the given system of inequalities as shown below by a polygon. This is called the feasible region.
There are 5 vertices: A, B, C, D and E. Each point is determined by solving the 2 by 2 system of equations corresponding to the two lines whose intersection is the vertex to be found (see example 2 above).
Point A is the intersection of lines x = 0 and y = 0. Solution A(0 , 0).
Point B is is the intersection of lines x = 0 and y = x + 1. Solution B(0 , 1)
Point C is is the intersection of lines y = x + 1 and 4 y + x = 10. Solution C(6/5 , 11/5)
Point D is is the intersection of lines 4y + x = 10 and y - x = - 3. Solution D(22/5 , 7/5)
Point E is is the intersection of lines y - x = -3 and y = 0. Solution E( 3 , 0)

.