-
A car traveled 281 miles in 4 hours 41 minutes. What was the average speed of the car in miles per hour?
Solution
We first convert the time of 4 hours 41 minutes in minutes
4 hours 41 minutes = 4 × 60 + 41 = 281 minutes
Average speed S is given by distance / time. Hence
S = 281 miles / 281 minutes = 1 mile / minute
= 60 miles / hour
-
In a group of 120 people, 90 have an age of more 30 years, and the others have an age of less than 20 years. If a person is selected at random from this group, what is the probability the person's age is less than 20?
Solution
Number of people whose age is less than 20 is given by
120 - 90 = 30
Probability P that a person selected at random from the group is less than 20 is gieven by
30 / 120 = 0.25
-
The length of a rectangle is four times its width. If the area is 100 m2 what is the length of the rectangle?
Solution
Let L be the length and W be the width of the rectangle. Hence
L = 4 W
We now use the area to write
100 = L × W
Substitute L by 4 W in the equation above
100 = 4 W × W = 4 W2
Solve for W and find L
4 W2 = 100
W2 = 25 , W = 5 and L = 4 W = 20 m
-
A six-sided die is rolled once. What is the probability that the number rolled is an even number greater than 2?
Solution
Out of the 6 possible numbers that may rolled, 3 are even: 2, 4 and 6 BUT only 4 and 6 are greater than 2. Hence the probability that the number rolled is an even number greater than 2 is given by
(number of even numbers greater than 2) / 6 = 2 / 6 = 1 / 3
-
Point A has the coordinates (2,2). What are the coordinates of its image point if it is translated 2 units up and 5 units to the left, and reflected in the x axis?
Solution
A translation of 2 units up will increase the y coordinate by 2 units and a translation by 5 units to the left will decrease the x coordinate by 5. Hence after these translations point (2,2) becomes
(2 - 5 , 2 + 2) = (-3 , 4)
When point (-3 , 4) is reflected in the x axis, its y coordinate changes sign and point (-3 , 4) becomes
(-3 , -4)
-
The length of a rectangle is increased to 2 times its original size and its width is increased to 3 times its original size. If the area of the new rectangle is equal to 1800 square meters, what is the area of the original rectangle?
Solution
If L and W be the original length and width of the rectangle and its area is given by
L × W
After increase the length becomes 2 L and the width becomes 3 W. The area is then given by (2 L) × (3 W) and is known. Hence
(2 L) × (3 W) = 1800
Solve the above equation to find L × W
6 L × W = 1800
L × W = 1800 / 6 = 300 square meters , area of original rectangle
-
Each dimension of a cube has been increased to twice its original size. If the new cube has a volume of 64,000 cubic centimeters, what is the area of one face of the original cube?
Solution
Let x be the length of the edge of the original cube. When increased to twice its original size it becomes 2 x which gives a volume of
2x × 2x × 2x = 8x3
The volume is known. Hence
8x3 = 64,000
x3 = 8,000 which gives x = 20
The area of one face of the original (before the increase) is given by x2
x2 = 202 = 400 square centimeters
-
Pump A can fill a tank of water in 5 hours. Pump B can fill the same tank in 8 hours. How long does it take the two pumps working together to fill the tank?(round your answer to the nearest minute).
Solution
In 1 hour pump A can fill 1/5 of a tank and pump B can fill 1/8 of the same tank. So in 1 hour the two pumps working together can fill
1/5 + 1/8 = 13 / 40 of a tank
Since the rate of the two pumps working together is 13/40, the time t needed to fill the tank by the two pumps is found by solving
(13/40) t = 1
t = 40 / 13 = 39/13 + 1/13 hours
= 3 hours and (1/13)*60 minutes
= 3 hours 5 minutes (rounded to the nearest minute)
-
A water tank, having the shape of a rectangular prism of base 100 square centimeters, is being filled at the rate of 1 liter per minute. Find the rate at which the height of the water in the water tank increases. Express your answer in centimeters per minute.
Solution
The volume of a rectangular prism is given by
area of base × height
The rate at which the tank is being filled is 1 liter per minute which we need to convert
1 liter = 1 dm3
But 1 dm = 10 cm. Hence
1 liter = (10 cm)3 = 1000 cm3
The height h of the water is related to the volume by
volume = area of base × h
In one minute the volume increases by 1 liter or 1000 cm3 and the height increases by
h = volume / area of base = 1000 cm3 / 100 cm2 = 10 cm
-
Dany bought a total of 20 game cards some of which cost $0.25 each and some of which cost $0.15 each. If Dany spent $4.2 to buy these cards, how many cards of each type did he buy?
Solution
Let X be the number of cards that cost $0.25 each and Y the number of cards that cost $0.15 each. The total number of cards is 20. Hence
X + Y = 20
If X is the number of cards at $0.25, then the X cards cost
0.25 X
If Y is the number of cards at $0.15, then the Y cards cost
0.15 Y
The total cost of the X cards and the the Y cards is known to be $4.2 and also given by
0.25 X + 0.15 Y = 4.2
We now need to solve the system of equations
X + Y = 20
0.25 X + 0.15 Y = 4.2
The first equation gives Y = 20 - X. Substitute y by 20 - x in the second equation and solve
0.25 X + 0.15 (20 - X) = 4.2
X(0.25 - 0.15) + 3 = 4.2
0.1 X = 1.2
X = 12 and Y = 20 - 12 = 8
-
The size of the perimeter of the square ABCD is equal to 100 cm. The length of the segment MN is equal to 5 cm and the triangle MNC is isosceles. Find the area of the pentagon ABNMD.
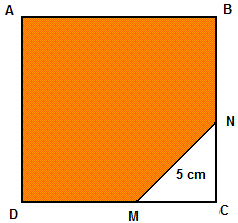
Solution
The area A of the pentagon ABNMD may found by subtracting the area of traingle MNC from the total area of the square.
A = 252 - (1/2) × MC × NC
Since triangle MNC is isosceles, the length of NC and MC are equal (MC = NC) and the above area may be written as.
A = 252 - (1/2) × MC2
Also triangle MNC is a right triangle. Let us use Pythagora's to find MC2.
MC2 + NC2 = 52
Since MC = NC, the above equation may be written as.
2 MC2 25
MC2 = 25 / 2
We now substitute MC2 by 25 / 2 in the area A found above
A = 252 - 25 / 4 = 625 - 6.25 = 618.75 square centimeters
-
Water is being pumped, at a constant rate, into an underground storage tank that has the shape of a rectangular prism. Which of the graphs below best represent the changes in the height of water in the tank as a function of the time?

Solution
When water is pumped into a tank, the height of the water will increase. The graph in the top right side shows a decreasing height and the graph at the bottom right shows a constant height and cannot therefore represent the height as a function of time. The graph at the top left is not the graph of a function. The only graph that may represent the height of the water in the tank being filled is the graph in the bottom left which shows an increasing height.
-
Initially the rectangular prism on the left was full of water. Then water was poured in the right cylindrical container so that the heights of water in both containers are equal. Find the height h of water in both containers.(round your answer to the nearest tenth of a cm).

Solution
The volume of water in the rectangular prism in the left is given by
2 × 4 × 10 = 80 cm3
The volume of water in the middle rectangular prism in given by
2 × 4 × h = 8 h
The volume of water in cylinder on the right is given by
Pi × (1)2 × h = Pi × h , Pi = 3.14
Since all water in the container on the left is poured in both containers on the right, then
80 cm3 = 8 h + Pi × h
Solve to find h
h = 80 / (8 + Pi)
h = 7.2 cm (rounded to the nearest tenth of a cm)
-
Peter drove at a constant speed for 2 hours. He then stopped for an hour to do some shopping and have a rest and then drove back home driving at a constant speed. Which graph best represents the changes in the distance from home as Peter was driving?
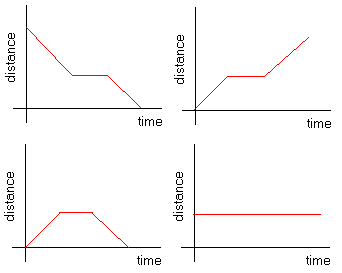
Solution
As peter drives away from home, the distance from home should increase. Only the graphs bottom-left and top-right shows an increase at the start (t=0). While shopping the distance stays constant but as he starts driving back the distance must decrease as he approaches home. Therefore only the graph at the bottem-left shows a decrease of distance and best represents the changes in the distance.
-
Two balls A and B rotate along a circular track. Ball A makes 2 full rotations in 26 minutes. Ball B makes 5 full rotation in 35 minutes. If they start rotating now from the same point, when will they be at the same starting point again?
Solution
If ball A makes 2 rotations in 26 minutes, it makes 1 rotation in 13 minutes. If ball B makes 5 rotations in 35 minutes, it makes 1 rotation in 7 minutes.
The two balls start rotating now and makes several rotations before they are at the SAME starting points. Ball A would have done a WHOLE number X of rotations and ball B would have done a WHOLE number Y of rotations. Also they would have rotated during the same period of time T. Hence
T = 13 X = 7 Y
Hence 13 X = 7 Y
Solve the above for X
X = 7 Y / 13
We want the time when they are FIRST at the same starting point. Therefore X and Y are the smallest whole numbers of the equation X = 7 Y / 13. The smallest value of Y that gives X as a whole number is 13. Hence
X = 7 (13) / 13 = 7
Time T is given by
T = 13 X = 13 × 7 = 91 minutes = 1 hour and 31 minutes
or T = 7 Y = 7 × 13 = 91 minutes = 1 hour and 31 minutes
-
In a certain college, 40% of the senior class students are taking Physics, 30% are taking calculus and 10% are taking both. If 40 students are enrolled in the senior class, how many students are taking neither Physics nor calculus?
-
Joe drove at the speed of 45 miles per hour for a certain distance. He then drove at the speed of 55 miles per hour for the same distance. What is the average speed for the whole trip?
-
If the radius of a cylindrical container is doubled, how do you change the height of the container so that the volume will stay the same?
-
One leg of a right triangle is 18 cm and its area is 108 square cm. Find its primeter.
-
What is the sum of the sizes of the interior angles of a polygon with 53 sides?
-
Jack is taller than Sarah but shorter than both Malika and Tania. Malika is shorter than tania. Natasha is shorter than Sarah. Who is the shortest?
-
What is the height (one of the legs) and the hypotenuse of an isosceles right triangle that has an area of 800 square feet?
-
Find the circumference of a circle inscribed inside a square with a side of 20 meters.
-
Two different schools (A and B) have the same number of pupils. The ratio of the boys in school A and the boys in school B is 2:1 and the ratio of the girls in school A and the girls in school B is 4:5. Find the ratio of the boys in school A to the girls in school A.
-
A water tank has the shape of a rectangular prism of base 50 cm2. This tank is being filled at the rate of 12 liters per minutes. Find the rate at which the height of the water in the water tank increases; express your answer in millimeters per second.
-
One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take each pump working alone to fill the tank?
Answers to the Above Questions
- 60 miles per hour
- 0.25
- 20 meters
- 1/3
- (-3,-4)
- 300 square meters
- 400 square cm
- 3 hours and 5 minutes
- 10 cm per minute
- 12 cards at $0.25 and 8 cards at $0.15
- 618.75 square cm
- graph at the bottom left
- 7.2 cm
- graph at the bottom left
- After 1 hour and 31 minutes
- 16 students
- 49.5 miles per hour
- 1/4 of the original height
- 51.6 cm
- 9180°
- Natasha
- height (leg) = 40 feet , hypotenuse = 40 √(2) feet
- 20? meters
- ratio of the boys in school A to the girls in school A is 1:2
- 40 mm/second
- faster pump: 27 minutes, slower pump: 54 minutes