Geometry Problems
With Solutions and Explanations for Grade 9

Detailed solutions and full explanations to Geometry Problems for grade 9 are presented.

  1. Angles A and B are complementary and the measure of angle A is twice the measure of angle B. Find the measures of angles A and B,
    Solution
    Let A be the measure of angle A and B be the measure of angle B. Hence
    A = 2B
    Angles A and B are complementary; hence
    A + B = 90°
    But A = 2B; hence
    2B + B = 90
    3B = 90
    B = 90 / 3 = 30°
    A = 2B = 60°

  2. ABCD is a parallelogram such that AB is parallel to DC and DA parallel to CB. The length of side AB is 20 cm. E is a point between A and B such that the length of AE is 3 cm. F is a point between points D and C. Find the length of DF such that the segment EF divide the parallelogram in two regions with equal areas.

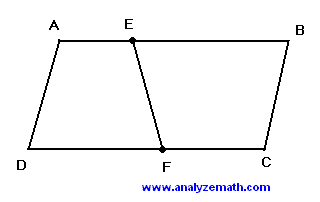    geometry problem 2 .


    Solution
    Let A1 be the area of the trapezoid AEFD. Hence
    A1 = (1/2) h (AE + DF) = (1/2) h (3 + DF) , h is the height of the parallelogram.
    Now let A2 be the area of the trapezoid EBCF. Hence
    A2 = (1/2) h (EB + FC)
    We also have
    EB = 20 - AE = 17 , FC = 20 - DF
    We now substitute EB and FC in A2 = (1/2) h (EB + FC)
    A2 = (1/2) h (17 + 20 - DF) = (1/2) h (37 - DF)
    For EF to divide the parallelogram into two regions of equal ares, we need to have area A1 and area A2 equal
    (1/2) h (3 + DF) = (1/2) h (37 - DF)
    Multiply both sides by 2 and divide thm by h to simplify to
    3 + DF = 37 - DF
    Solve for DF
    2DF = 37 - 3
    2DF = 34
    DF = 17 cm

  3. Find the measure of angle A in the figure below.

    geometry problem 3 .


    Solution
    A first interior angle of the triangle is supplementary to the angle whose measure is 129° and is equal to
    180 - 129 = 51°
    A second interior angle of the triangle is supplementary to the angle whose measure is 138° and is equal to
    180 - 138 = 42°
    The sum of all three angles of the triangle is equal to 180°. Hence
    A + 51 + 42 = 180
    A = 180 - 51 - 42 = 87°

  4. ABC is a right triangle. AM is perpendicular to BC. The size of angle ABC is equal to 55 degrees. Find the size of angle MAC.

    geometry problem 4 .


    Solution
    The sum of all angles in triangle ABC is equal to 180°. Hence
    angle ABC + angle ACM + 90° = 180°
    Substitute angle ABC by 55 and solve for angle ACM
    angle ACM = 180 - 90 - 55 = 35°
    The sum of all angles in triangle AMC is equal to 180°. Hence
    angle MAC + angle ACM + 90° = 180°
    Substitute angle ACM by 35 and Solve for angle MAC
    angle MAC = 180 - 90 - angle ACM = 180 - 90 - 35 = 55°

  5. Find the size of angle MBD in the figure below.

    geometry problem 5 .


    Solution
    The sum of all angles in triangle AMC is equal to 180°. Hence
    56 + 78 + angle AMC = 180
    angle AMC = 180 - 56 - 78 = 46°
    Angles AMC and DMB are vertical angles and therefore equal in measures. Hence
    angle DMB = 46°
    The sum of angles of triangle DMB is equal to 180°. Hence
    angle MBD + angle DMB + 62 = 180
    Substitute angle DMB by 46 and solve for angle MBD.
    angle MBD + 46 + 62 = 180
    angle MBD = 180 - 46 - 62 = 72°

  6. The size of angle AOB is equal to 132 degrees and the size of angle COD is equal to 141 degrees. Find the size of angle DOB.

    geometry problem 6 .


    Solution
    angle AOB = 132 and is also the sum of angles AOD and DOB. Hence
    angle AOD + angle DOB = 132° (I)
    angle COD = 141 and is also the sum of angles COB and BOD. Hence
    angle COB + angle DOB = 141° (II)
    We now add the left sides together and the right sides together to obtain a new equation.
    angle AOD + angle DOB + angle COB + angle DOB = 132 + 141 (III)
    Note that.
    angle AOD + angle DOB + angle COB = 180°
    Substitute angle AOD + angle DOB + angle COB in (III) by 180 and solve for angle DOB.
    180 + angle DOB = 132 + 141
    angle DOB = 273 - 180 = 93°

  7. Find the size of angle x in the figure.

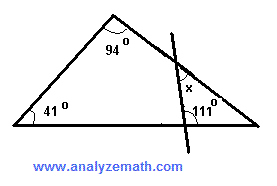    geometry problem 7 .


    Solution
    The interior angle of the quadrilateral on the left that is supplementary to x is equal to
    180 - x
    The interior angle of the quadrilateral on the left that is supplementary to the angle of measure 111° is equal to
    180 - 111 = 69°
    The sum of all interior angles of the quadrilateral is equal to 360°. Hence
    41 + 94 + 180 - x + 69 = 360
    Solve for x
    41 + 94 + 180 - x + 69 = 360
    384 - x = 360
    x = 384 - 360 = 24°

  8. The rectangle below is made up of 12 congruent (same size) squares. Find the perimeter of the rectangle if the area of the rectangle is equal to 432 square cm.

    geometry problem 8.


    Solution
    If the total area of the rectangle is 432 square cm, the area of one square is equal to
    432 / 12 = 36 square cm
    Let x be the side of one small square. Hence the area of one small circle equal to 36 gives
    x2 = 36
    Solve for x
    x = 6 cm
    The length L of the perimeter is equal to 4x and the width W is equal to 3x. Hence
    L = 4 × 6 = 24 cm and W = 3 × 6 = 18 cm
    The perimeter P of the rectangle is given by
    P = 2 (L + W) = 2(24 + 18) = 84 cm

  9. ABC is a right triangle with the size of angle ACB equal to 74 degrees. The lengths of the sides AM, MQ and QP are all equal. Find the measure of angle QPB.

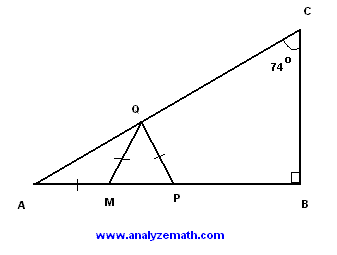    geometry problem 9 .


    Solution
    Angle CAB in the right triangle ACB is given by
    90 - 74 = 16°
    Sides AM and MQ in size and therefore triangle AMQ is isosceles and therefore
    angle AQM = angle QAM = 16°
    The sum of all interior angles in triangle AMQ is equal to 180°. Hence
    16 + 16 + angle AMQ = 180
    Solve for angle AMQ
    angle AMQ = 180 - 32 = 148°
    Angle QMP is supplementary to angle AMQ. Hence
    angle QMP = 180 - angle AMQ = 180 - 148 = 32°
    Lengths of QM and QP are equal; hence triangle QMP is isosceles and therefore angle QPM is equal in size to angle QMP. Hence
    angle QPM = 32°
    Angle QPB is supplementary to angle QPM. Hence
    angle QPM = 180 - angle QPM = 180 - 32 = 148°

  10. Find the area of the given shape.

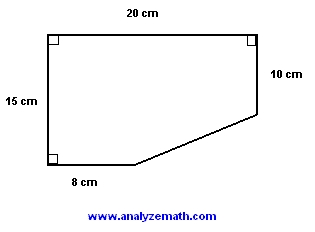    geometry problem 10 .


    Solution
    The area of the given shape may be found by subtracting the area of the right triangle (red) from the area of the large rectangle (see figure below).

    solution to geometry problem 10 .


    Sides of the right triangle (red) are given by
    15 - 10 = 5 cm and 20 - 8 = 12 cm
    Area of given shape = 20 × 15 - (1/2) × 12 × 5 = 270 cm2

  11. Find the area of the shaded region.

    geometry problem 11 .


    Solution
    The area of the given shape may be found by subtracting the area of the rectangle at the top left from the area of the large rectangle.
    Dimensions of the rectangle at top left
    length = 30 - 8 = 22 cm , width = 15 - 4 = 11 cm
    Area of given shape = 30 × 15 - 22 × 11 = 208 cm2

  12. The vertices of the inscribed (inside) square bisect the sides of the second (outside) square. Find the ratio of the area of the outside square to the area of the inscribed square.

    geometry problem 12.


    Solution
    Let 2 x be the size of the side of the large square (see figure below).

    solution geometry problem 12.

    The area of the large square is
    (2 x ) × ( 2x) = 4 x 2
    The area of the inscribed square is
    y × y = y 2
    Use of Pythagora's theorem gives
    y 2 = x 2 + x 2 = 2 x2
    Ratio R of the area of the outside square to the area of the inside square is given by
    R = 4 x 2 / y 2 = 4 x 2 / 2 x 2 = 4 / 2 = 2 / 1

Answers to the Above Questions

  1. measure of A = 60 degrees, measure of B = 30 degrees
  2. length of DF = 17 cm
  3. measure of A = 87 degrees
  4. size of angle MAC = 55 degrees
  5. size of angle MBD = 72 degrees
  6. size of angle DOB = 93 degrees
  7. size of angle x = 24 degrees
  8. perimeter of large rectangle = 84 cm
  9. measure of angle QPB = 148 degrees
  10. area of given shape = 270 square cm
  11. area of shaded region = 208 square cm
  12. ratio of area of outside square to area of inscribed square = 2:1

More References and Links

More Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
More High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
More Primary Math (Grades 4 and 5) with Free Questions and Problems With Answers
Home Page
{ezoic-ad-1}
{ez_footer_ads}