Convert Polar to Rectangular Coordinates and Vice Versa

The rectangular coordinates (x , y) and polar coordinates (R , t) are related as follows.
y = R sin t    and    x = R cos t
R 2 = x 2 + y 2    and    tan t = y / x

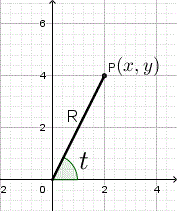
polar-rectangular conversion of coordinates.

To find the polar angle t, you have to take into account the sings of x and y which gives you the quadrant.
Angle t is in the range [0 , 2π) or [0 , 360°).

Examples on Converting Polar and Rectangular Coordinates

Example 1

Convert the polar coordinates (5 , 2.01) and (0.2 , 53°) to rectangular coordinates to three decimal places.

Solution to Example 1

  • For the first point (5 , 2.01), R = 5 and t = 2.01 and is in radians. Set your calculator to radians and use the above formulas for x and y in terms of R and t to obtain:
    x = R cos t = 5 cos 2.01 = -2.126
    y = R sin t = 5 sin 2.01 = 4.525
  • For the second point (0.2 , 53°), R = 0.2 and t = 53° and is in degrees. Set your calculator to degrees and use the above formulas for x and y in terms of R and t to obtain:
    x = R cos t = 0.2 cos 53° = 0.120
    y = R sin t = 0.2 sin 53° = 0.160

Example 2

Convert the rectangular coordinates (1 , 1) and (-2 ,-4) to polar coordinates to three decimal places. Express the polar angle t in degrees and radians.

Solution to Example 2

  • We first find R using the formula R = √ [x 2 + y 2] for the point (1 , 1).
    R = √ [x 2 + y 2] = √ [1 + 1] = √ ( 2 )
  • We now find tan t using the formula tan t = y / x.
    tan t = 1 / 1
  • Using the arctan function of the calculator, we obtain.
    t = Pi / 4 or t = 45 o
  • Point (1 , 1) in rectangular coordinates may be written in polar for as follows.
    ( √ ( 2 ) , π / 4 ) or ( √ ( 2 ) , 45 o )

  • Let us find find R using for the point (-2 , -4).
    R = √ [x 2 + y 2] = √ [4 + 16] = √ ( 20 ) = 2 √ ( 5 )
  • We now find tan t.
    tan t = - 4 / - 2 = 2

  • Using the arctan function of the calculator, we obtain.
    t = 1.107 or t = 63.435 o
  • BUT since the rectangular coordinates x and y are both negative, the point is in quadrant III and we need to add π or 180° to the value of t given by the calculator. Hence the polar angle t is given by
    t = 4.249 or t = 243.435°
  • Point (-2 , -4) in rectangular coordinates may be written in polar for as follows.
    ( 2 √ ( 5 ) , 4.249 ) or ( 2 √ ( 5 ) , 243.435° )

More References and Links to Polar Coordinates and Trigonometry

Convert Polar to Rectangular Coordinates Calculator .
Polar Coordinates.
Trigonometry Tutorials and Problems.

Search