Vertex and Intercepts Parabola Problems


A set of problems, with detailed solutions, related to the vertex and intercepts of parabolas are presented.



SEARCH THIS SITE

Google

Review
The graph of a quadratic function of the form

f(x) = a x 2 + b x + c

is a parabola with vertex at the point (h , k).

where h = - b / 2a
and
and k = f(h) = c - b 2 / 4a

Also the x intercepts (if any) of the graph of f are given by

x1 = [ - b + sqrt (b 2 - 4 a c) ] / 2 a

and

x2 = [ - b - sqrt (b 2 - 4 a c) ] / 2 a

It can be easily shown that h = (x1 + x2) / 2

If the graph of f has x intercepts at x1 and x2 then x1 and x2 are solutions to the equation f(x) = 0 so that f may be given by

f(x) = a (x - x1) (x - x2)

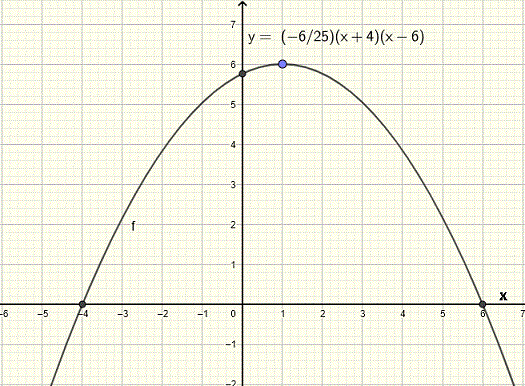
Problem 1 : Find the quadratic function whose graph, which is a parabola, has x intercepts at x = - 4 and x = 6, and its highest point has a y coordinate equal to 5.

Solution to Problem 1:

The x intercepts are given as - 4 and 6 hence f may be written as

f(x) = a (x - (-4)) (x - 6)

The highest point is the vertex. If x1 and x2 are the x intrcepts of the graph then the x coordinate h of the vertex is given by

h = (x1 + x2) / 2 = (- 4 + 6) / 2 = 1

We now know the x (h = 1) and y coordinates (k = 6) of the vertex which is a point on the graph of the parabola. Hence

f( 1 ) = 6

When f( 1 ) = 6 is substituted in f(x) = a (x - (-4)) (x - 6), it gives

a (1 + 4)(1 - 6) = 6

Solve for a to find

a = - 6 / 25

The equation of the parabola is given by

f(x) = ( - 6 / 25) (x + 4) (x - 6)

Problem 2 : A parabola, with verical axis, has a vertex at (1 , - 8) and passes through the point (2 , - 6). Find the x intercepts of this parabola.

Solution to Problem 2:

If h and k are the coordinates of the vertex, the quadratic function in vertex form corresponding to this parabola is given by

f(x) = a (x - h) 2 + k

= a (x - 1) 2 - 8

Use the fact that (2 , - 6) is a point on the graph of the parabola to find coefficient a

- 6 = a (2 - 1) 2 - 8

Solve for a to obtain

a = 2

The equation of the parabola is given by

f(x) = 2 (x - 1) 2 - 8

The x intercepts of the parabola are found by solving

f(x) = 0

Hence

2 (x - 1) 2 - 8 = 0

Solve for x

2 (x - 1) 2 - 8 = 0

2 (x - 1) 2 = 8

(x - 1) 2 = 4

solutions to above equation are

x = 3 and x = -1

The x intercepts are at the points : (3 , 0) and (-1 , 0).

Problem 3 : A quadratic function has a minimum value of - 2 and its graph has y intercept at (0 , 6) and x intercept at (3 , 0). Find a possible equation for this quadratic function.

Solution to Problem 2:

The minimum value of a quadratic function is equal to k in the quadratic function in vertex form which is given by

f(x) = a (x - h) 2 + k

= a (x - h) 2 - 2

We now use the y intercept (0 , 6) given above

6 = a (0 - h) 2 - 2 = a h 2 - 2

Solve the above equation for a

a = 8 / h 2

Use the x intercept (3 , 0) given in the problem above

0 = a (3 - h) 2 - 2

Substitute a = 8 / h 2 into the above equation to obtain

0 = ( 8 / h 2 )(3 - h) 2 - 2

Eliminate the denominators to obtain a quadratic equation in h

h 2 - 8 h + 12 = 0

Solve the above equation for h

h = 6 and h = 2.

Use a = 8 / h 2 to find the corresponding values of a

when h = 6 , a = 2 / 9

and when h = 2 , a = 2

The two quadratic functions that are solutions are given by

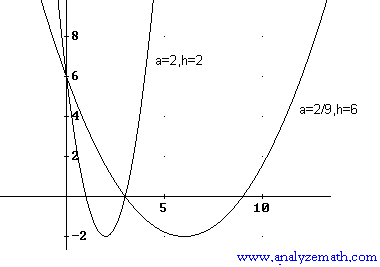
f(x) = 2 (x - 2) 2 - 2

f(x) = (2 / 9) (x - 6) 2 - 2

The graphs (parabolas) of the two quadratic functions obtained are shown below. Check that they have the same x , y intrcepts and minimum value.

graph solution problem 3

More Online Tutorials on Functions and Algebra.

Home Page - Online Calculators - Trigonometry - Antennas - Graphing - Precalculus Tutorials - Calculus Tutorials
Calculus Questions - Geometry Tutorials - Precalculus Applets - Applied Math - Precalculus Questions and Problems -
Equations, Systems and Inequalities - Geometry Calculators - Math Software - Elementary Statistics -
Author - e-mail
Updated: 27 November 2007 (A Dendane)