Find Vertex and Intercepts of Quadratic Functions - Calculator
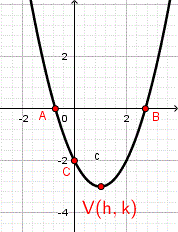
An easy to use calculator to find the vertex, x and y intercepts of the graph of a quadratic function and write the function in vertex form.
The quadratic function to be considered id of the form:
f(x) = ax2 + bx + c
Vertex of the graph of a Parabola
The vertex of the graph of a parabola is the maximum or minimum point of the graph. This online calculator uses the formulas
h = - b / 2a
and
k = f(h)
to find the x and y coordinates h and k,respectively, of the vertex of a parabola.
Figure 1. Graph of a parabola with x (points A and B) and y (point C) intercepts and the vertex V.
Knowing the x and y coordinates k and h of the vertex, the equation of the parabola in vertex form is given by:
f(x) = a(x - h)2 + k
x and y intercepts of the graph of a Parabola
To find the x intercepts, the calculator solves the quadratic equation ax2 + bx + c = 0 using the quadratic formulas:
x1 = (- b + √?) / (2 a)
x2 = (- b - √?) / (2 a)
where ? = b2 - 4 a c is the discriminant.
The y intercept is given by f(0) = c.
Use of Calculator to Find Vertex and Intercepts of Quadratic Functions
1 - Enter the coefficients a, b, c as real numbers and the number decimal places as an integer and press "Solve". The coordinates of the x and y intercepts are displayed.
If the two coordinates are equal, the graph touches the x axis and the two x intercepts have equal x coordinates. The x intercepts may not exist. The x and y coordinates of the vertex and the vertex form of the function are also displayed at the bottom.
