Tutorial on Rational Functions (1)

Solution to Example 1:

1. The graph has y intercepts at (0 , -1) , you can write
   f(0) = -1
   
   
   
2. Which leads to the equation
   -1 = 2 / c
   
   
3. Solve the above equation for c.
   c = -2
   
   
4. The vertical asymptote is given by the zero(s) of the denominator of the equation of the function. A vertical asymptote at x = 2 means that the denominator is equal to zero at x = 2. This leads to
   2b + c = 0
   
   
5. Substitute -2 for c
   2b - 2 = 0
   
   
6. and solve for b.
   b = 1.
   
   
7. The equation of f is given by
   f(x) = 2 / (x -2)
   
   
8. Check answer graphically. Below is shown the graph of f obtained. Check the y intercept and the vertical asymptote.
   
   
   

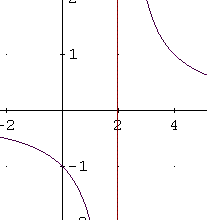
Matched Exercise 1: Find the equation of the rational function f of the form

Example 2 : Find the equation of the rational function f of the form

Solution to Example 2:

1. The x intercept(s) is the zero of the numerator. The numerator is equal to zero at x = 2
   2 + a = 0
   
   
2. Solve the above equation for a.
   a = -2
   
   
3. The horizontal asymptote is given by ratio of the leading coefficients in the numerator and denominator.
   1 / b = 1/2
   
   
4. Solve for b
   b = 2
   
   
5. The vertical asymptote is given by the zero of the denominator. At x = -1 the denominator in f(x) has to be equal to zero.
   -b + c = 0
   
   
6. Substitute 2 for b in the above equation
   -2 + C = 0
   
   
7. Solve the above equation for c
   c = 2
   
   
8. The equation of the rational function is given by
   f(x) = (x - 2)/(2x + 2)
   
   

Check answer graphically: The graph of the rational function obtained is shown below. Check the x intercept, the vertical and the horizontal asymptotes.

Matched Exercise 2: Find the equation of the rational function f of the form

More on rational functions can be found at

Graphs of rational functions

tutorial on graphs of rational functions

self test on graphs of rational functions.