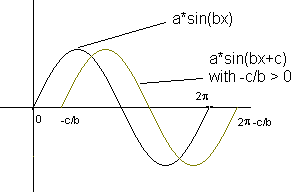|
|
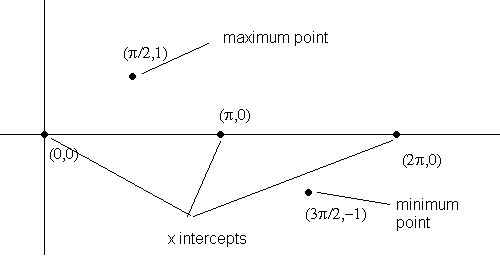
| Las propiedades tales como dominio, rango y las intersecciones de las gráficas de estas funciones son también examinó en detalle. Revisar En primer lugar, comenzar con la gráfica de la función seno de base f (x) = sen (x) El dominio de la función f es el conjunto de todos los números reales. El rango de f es el intervalo [-1,1]. -1 <= sen (x) <= 1 (<= significa menor o igual) También la función f es periódica con período igual a 2 p. La gráfica de f en un período puede ser esbozado por primera búsqueda de los puntos que dan información importante como x intercepta, intersección, máximos y mínimos. Hagamos una tabla de valores de la función f en el intervalo de un período de: [0, 2 p].
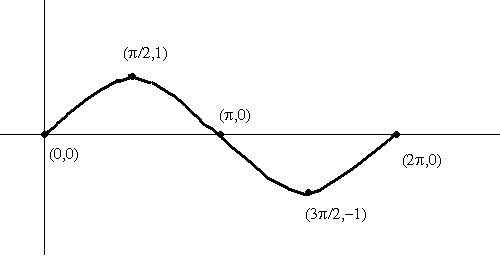
La elección de los valores de x en la tabla corresponden a X e intercepta y, máximos y puntos mínimos. Estos son los puntos útiles para representar gráficamente la función seno durante un período de: [0, 2 p].Para graficar f, primer gráfico los puntos en la tabla a continuación, participar en estos puntos. Por supuesto, usted puede añadir puntos extra si lo desea. Pero los cinco puntos utilizados son los puntos clave. Otro punto importante a destacar es que los 5 puntos clave de dividir el período en 4 partes iguales. Véanse las figuras de abajo.
Para tener una visión completa de por qué la gráfica de la sen (x) cambia con x como se muestra arriba, puede ir a través de un tutorial interactivo en el círculo unitario trigonométricas círculo unidad trigonométricas.
Graphing f (x) = a * sen (bx + c) En primer lugar, necesitamos entender cómo los parámetros a, b y c afectan a la gráfica de f (x) = a * sen (bx + c) cuando se compara con la gráfica de sen (x)? Es posible que desee pasar por un tutorial interactivo en funciones de seno. El dominio de f es el conjunto de todos los números reales. La gama de expresión bx + c es el conjunto de todos los números reales. Por lo tanto, el rango de sen (bx + c) es [-1,1]. Por lo tanto -1 <= sen (bx + c) <= 1 Multiplica ambos lados por a. Si a> 0 -a <= a * sen (bx + c) <= a Si a <0 (símbolos de cambio de la desigualdad) -a> = a*sen (bx + c) = a o <= a*sen (bx + c) <= - a
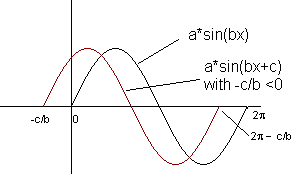
Podemos decir que el parámetro a afectar el rango de f, que se puede escribir como [- | a |, | a |]. | A | se llama la amplitud. Periodo de f Supongamos primero que c = 0 y f (x) = a * sen (bx). Para f para completar un ciclo (período), bx expresión debe variar de 0 a 2 p. 0 <= bx <= 2 p. Dividir todos los términos de la desigualdad por b. Si b> 0 0 <= x <= 2 p / b. Periodo = 2 p / b - 0 = 2 p / b. Si b <0 (símbolos de cambio de las desigualdades) 0> = x> = 2 p / b. Lo que equivale a 2 p / b <= x <= 0. Periodo = 0 - 2 p / b = - 2 p / b Uso de la notación de valor absoluto, podemos escribir el período de f = 2 p / | b |. Phase Shift Consideremos ahora el argumento de toda BX + C. Para f para completar un ciclo (período), la expresión bx + c tiene que variar de 0 a 2 p. 0 <= bx + c <= 2 p. Suponga que b> 0 y resolver para x -c <= bx <= 2 p-c. -c / b <= x <= 2 p / b - c / b. Período de f = 2 p / b - c / b - (-c / b) = 2 p / | b |. C no afecta a la época. Comparemos ahora el ciclo [0, 2 p / b] cuando c = 0 con el ciclo de [-c / b, 2 p / b - c / b]. Esto indica que hay un cambio de -c/b. -c/b se llama el cambio de fase. Si -c / b <0, el cambio será a la izquierda. Si -c/b> 0, el cambio será el de la derecha.
Ejemplo 1: f es una función dada por f (x) = 2sen (3x - p / 2)
a - Encontrar el dominio de f y el rango de f. b - Determinar el periodo y el cambio de fase de la gráfica de f. c - Dibuje la gráfica de la función f en un período. Respuesta a la Ejemplo 1 a - El dominio de f es el conjunto de todos los números reales. La gama está dado por el intervalo [-2, 2]. b - Período = 2 p / | b | = 2 p / 3 Diferencia de fase = - c / b = - (- p / 2) / 3 = P / 6 c - Para dibujar la gráfica de f en un período, tenemos que encontrar los 5 primeros puntos clave. Que 3x - p / 2 variar de 0 a 2 p, a fin de tener un período completo a continuación, encontrar los valores de f (x).Ver tabla de abajo.
Ahora tenemos que encontrar los valores correspondientes de x. La primera fila de la tabla de arriba da 0 <= 3x - p / 2 <= 2 p Resuelva para x p / 2 <= 3x <= 2 p + p / 2 p / 2 <= 3x <= 5p / 2 p / 6 <= x <= 5p / 6 Ahora completa el cuadro con los valores de x. Una vez que los valores de x p / 6 y 5p / 6 que describe toda una época se encuentran, los otros 3 puntos se encuentran las siguientes: El valor medio = (p / 6 + 5p / 6) / 2 = 3p / 6 Valor en el primer trimestre = (p / 6 + 3p / 6) / 2 = 2p / 6 Valor en el tercer trimestre = (3p / 6 + 5p / 6) / 2 = 4p / 6 Las fracciones no se han reducido, esto hará más fácil de escalar el eje x en unidades de P / 6 y gráfico de los puntos.
Ahora ponemos los puntos dados (x, f (x)) y unirse a ellos por una curva suave.
Igualados Problema: f es una función dada por f (x) = (1 / 2) sen (4x + p / 2)
a - Encontrar el dominio de f y el rango de f. b - Determinar el periodo y el cambio de fase de la gráfica de f. c - Dibuje la gráfica de la función f en un período.
Más referencias y enlaces a gráficos, gráficos de funciones y funciones de seno. |