| Una aplicación interactiva se utiliza para explorar las funciones logarítmicas y las propiedades de sus gráficas como de dominio, rango, intercepciones y asíntota vertical. Los parámetros incluidos en la definición de la función logarítmica se puede cambiar, utilizando controles deslizantes, para investigar sus propiedades. La continua (pequeños incrementos) los cambios de estos parámetros ayudan a obtener un profundo conocimiento de las funciones logarítmicas. La función a ser explorado tiene la forma f (x) = a * log B [b (x + c) + d] a, b, cyd son coeficientes y B es la base de los logaritmos.
Definición de la función logarítmica La función logarítmica se define como la inversa de la función exponencial.
Para B> 0 y B no es igual a 1,
y = log x B es equivalente a x = B y
Nota: El logaritmo en base e es ln escrito (x). Ejemplo - f (x) = log2 x
- g (x) = log4 x
- h (x) = log0,5 x
Tutorial interactivo (1)
1 - Haga clic en el botón de arriba ", haga clic aquí para empezar" y maximizar la ventana obtenidos. 2 - Utilice los controles deslizantes en la parte izquierda del panel de control del applet para establecer a = 1, b = 1, c = 0, d = 0 y B = 2. Estos valores definen la función f, en parte, a), del ejemplo anterior. Revise algunos puntos en el gráfico como log 2 1 = 0, registro de 2 2 = 1, log 2 4 = 2. Utilice el zoom dentro y fuera si es necesario. 3 - Mantener los mismos valores para a, b, c, y que el anterior y el conjunto B = 4 a definir la función g en el apartado b) anterior. 4 - Mantener los mismos valores para a, b, c, y que el anterior y el conjunto B = 0,5 a definir la función g en la parte c).
Dominio y rango de la función logarítmica Sea f (x) = log B x Dado que la función exponencial es la inversa de la función logarítmica, el rango de la función logarítmica es el dominio de la función exponencial, que es el conjunto de todos los números reales. El dominio de la función logarítmica es el rango de la función exponencial, dada por el intervalo (0, + infinito). Tutorial interactivo (2) 1 - Utilice los controles deslizantes en la parte izquierda del panel de control del applet para establecer a = 1, b = 1, c = 0, d = 0 y cambio de base B. Observar el dominio y el rango de la función logarítmica.
Vertical asíntota de la función logarítmica log B 0 es indefinido. Sin embargo, es posible investigar el comportamiento de la gráfica de la función logarítmica a medida que x se acerca a cero por la derecha (x> 0). Ejemplo Sea f (x) = log 3 x, y encontrar los valores de f (x) cuando x se aproxima a cero. Los resultados se muestran en el cuadro siguiente. 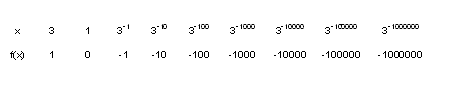 Cuando x se acerca a cero, f (x) decrece sin límite. En el gráfico se acerca al eje y (x = 0). La línea vertical x = 0 se denomina a la asíntota vertical. Tutorial interactivo (3) 1 - Utilice los controles deslizantes en la parte izquierda del panel de control del applet para establecer a = 1, b = 1, c = 0, d = 0 y el cambio de la base. Observar el comportamiento de la gráfica cerca del eje y.
El cambio, de escala y reflexión de la gráfica de funciones logarítmicas Tutorial interactivo (4) Respuestas y soluciones a Tutorial (4) . 1 - Investigar base B: set a = 1, b = 1, c = 0 y d = 0 usando la barra de desplazamiento. La serie B con valores entre 0 y 1 y con los valores mayores que uno, tome nota de los diferentes gráficos obtenidos y explicar. 2 - Investigar los efectos de un parámetro de escala (vertical) mediante el establecimiento de B = e, b = 1, c = 0 y d = 0. 3 - Investigar los efectos del parámetro b (escala horizontal) mediante el establecimiento de un = 1, c = 0, d = 0 y B = e. 4 - el conjunto B = E, A = 1, b = 1 e investigar los efectos de la c (horizontal cambiando) y D (traslación vertical). 5 - de la serie B, A y D para algunos valores y explicar cómo los parámetros b y c afectar al dominio de la función logarítmica. Explique analíticamente. 6 - ¿Qué parámetro (s) x afectar a la intercepción? ¿Siempre hay una x intercepción? Explique analíticamente. 7 - ¿Qué parámetro (s) afectan a la intersección y? ¿Hay siempre ay intercepción? Explique analíticamente. 8 - ¿Qué parámetro (s) afectan a la asíntota vertical? Explique analíticamente. Más tutoriales y pruebas de autoevaluación sobre las funciones logarítmicas.
Calcular Exponenciales y logaritmos a cualquier Base: .
graficación de funciones logarítmicas .
Comprobación automática en la solución de ecuaciones logarítmicas .
Tutoriales sobre Solución de ecuaciones logarítmicas .
Auto prueba gráfica de funciones logarítmicas . |