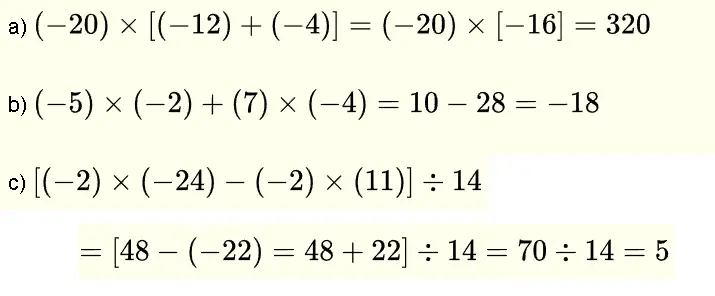Loading [MathJax]/extensions/tex2jax.js
Soluciones al Examen de Práctica de Matemáticas de 7º Grado
Se presentan las soluciones a las preguntas del examen de práctica de matemáticas de 7º grado.
1 - Números Enteros
Soluciones
-
El valor absoluto de un número es siempre positivo o cero, por lo que solo la parte b) es verdadera.
Todos los números involucrados en las desigualdades dadas están representados en la recta numérica a continuación. Dados dos números en la recta numérica, el que está a la derecha es mayor que el que está a la izquierda o viceversa.
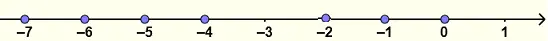
Por lo tanto:
a)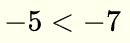 
NO ES VERDADERO (-5 a la derecha de - 7) b) 
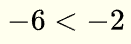ES VERDADERO ,
c)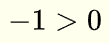 
NO ES VERDADERO (-1 a la izquierda de 0) d) 
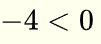ES VERDADERO
-
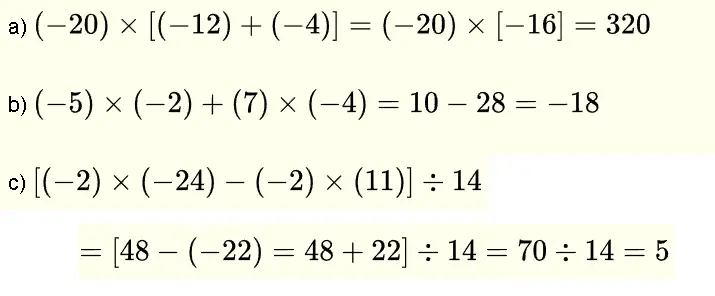
2 - Decimales
Soluciones
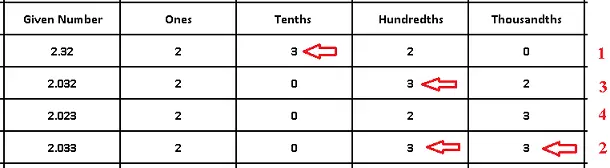
Escribe los números en una tabla que incluya el valor posicional como se muestra a continuación
\( \)\( \)\( \)\( \)
\( \require{cancel} \)
1) Comparamos los dígitos en las unidades y todos son iguales
2) Luego comparamos las décimas y la más alta es la correspondiente al número en la primera fila. \( 2.32 \) es el más grande.
3) Luego comparamos los centésimos y los dos más altos están en la segunda y cuarta filas.
4) Luego comparamos los milésimos de los números en la segunda y cuarta filas y el de la cuarta fila es el más alto. \( 2.033 \) es el segundo más grande.
5) \( 2.032 \) es el tercero más grande y \( 2.032 \) es el cuarto más grande.
El orden de mayor a menor es: \( 2.32 \), \( 2.033 \), \( 2.032 \), \( 2.023 \)
a) \( 4.01 \) tiene un \( 0 \) en las décimas, por lo tanto, no hay cambio en las unidades y, por lo tanto, la respuesta es \( 4 \)
b) \( 6.8 \) tiene un \( 8 \) en las décimas, por lo tanto, sumamos \( 1 \) a las unidades y, por lo tanto, la respuesta es \( 7 \)
c) \( 11.5 \) tiene un \( 5 \) en las décimas, por lo tanto, sumamos \( 1 \) a las unidades y, por lo tanto, la respuesta es \( 12 \)
a) \( 0.15 \div 3 = 0.05\)
b) \( 5 - 1.2 \times 0.2 = 5 - 0.24 = 4.76 \)
c) \( 2.3 - 0.7 \div 7 = 2.3 - 0.1 = 2.2\)
3 - Factores, Múltiplos y Divisibilidad de Números
Soluciones
Los factores de \( 18 \) son: \( 1, 2, 3, \color{red}6, 9, 18 \)
Los factores de \( 24 \) son: \( 1, 2, 3, 4, \color{red}6, 8, 12, 24 \)
El Mayor Común Factor (MCF) de \( 24 \) y \( 18 \) es \( \color{red}6 \)
Los múltiplos de \( 8\) son: \( 8, 16, 24, 32, 40, 48, 56, 64,\color{red}{72}, 80 \)
Los múltiplos de \( 18 \) son: \( 18, 36, 54, \color{red}{72}, 90 \)
El Mínimo Común Múltiplo (MCM) de \( 8 \) y \( 18 \) es \( \color{red}{72} \)
Un número cuyo último dígito en las unidades (más a la derecha) es \( 0 \) o \( 5 \) es divisible por \( 5 \).
Por lo tanto, los números en la parte b) \( 303090 \) y c) \( 145055 \) son divisibles por \( 5 \).
Un número cuyo último dígito en las unidades (más a la derecha) es \( 0, 2, 4, 6 , 8 \) es divisible por \( 2 \).
Por lo tanto, los números en la parte a) \( 2798 \) y c) \( 6476 \) son divisibles por \( 2 \).
Un número es divisible por \( 3 \) si la suma de todos sus dígitos en el número es divisible por \( 3 \) (o es un múltiplo de \( 3 \))
a) \( 9240 \) : suma de dígitos: \( 9+2+4+0 = 15 \) , \( 15 \) es divisible por \( 3 \) y, por lo tanto, \( 9240 \) es divisible por 3.
b) \( 4 909 \): suma de dígitos: \( 4+9+0+9 = 22 \) , \( 22 \) no es divisible por \( 3 \) y, por lo tanto, \( 4 909 \) NO es divisible por 3.
c) \( 3 282 900 \) : suma de dígitos: \( 3+2+8+2+9+0+0 = 24 \) , \( 24 \) es divisible por \( 3 \) y, por lo tanto, \( 3 282 900 \) es divisible por 3.
4 - Fracciones y Números Mixtos
Soluciones
Podemos obtener una fracción equivalente a una dada multiplicando o dividiendo el numerador y el denominador de la fracción dada por el mismo número.
a)
Dada \( \displaystyle \frac{10}{15} = \frac{?}{3} \)
Para pasar de un denominador igual a \( 15 \) en la fracción de la izquierda a un denominador igual a \( 3 \) en la fracción de la derecha, dividimos por \( 5 \). Por lo tanto,
\( \displaystyle \frac{10}{15} = \frac{10 \color{red}{\div 5}}{15 \color{red}{\div 5}} = \frac{2}{3} \)
b)
Dada \( \displaystyle \frac{17}{3} = \frac{34}{?} \)
Para pasar de un numerador igual a \( 17 \) en la fracción de la izquierda a un numerador igual a \( 34 \) en la fracción de la derecha, multiplicamos por \( 2 \). Por lo tanto,
\( \displaystyle \frac{17}{3} = \frac{17 \color{red}{\times 2} }{3 \color{red}{\times 2} } = \frac{34}{6} \)
c)
Dada \( \displaystyle \frac{11}{2} = \frac{?}{8} \)
Para pasar de un denominador igual a \( 2 \) en la fracción de la izquierda a un denominador igual a \( 8 \) en la fracción de la derecha, multiplicamos por \( 4 \). Por lo tanto,
\( \displaystyle \frac{11}{2} = \frac{11 \color{red}{\times 4}}{2 \color{red}{\times 4}} = \frac{44}{8} \)
a)
Convierte la fracción \( \displaystyle \frac{2}{5} \) a una fracción equivalente con denominador igual a \( 10 \)
\( \displaystyle \frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10} \)
Sustituye la fracción \( \displaystyle \frac{2}{5} \) por su equivalente en la expresión dada
\( \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} = \frac{4}{10} + \frac{3}{10} - \frac{1}{10} \)
Las fracciones en la suma/resta tienen el mismo denominador y, por lo tanto, las sumamos/restamos de la siguiente manera
\( \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} = \frac{4}{10} + \frac{3}{10} - \frac{1}{10} \\
= \displaystyle \frac{4}{10} + \frac{3}{10} - \frac{1}{10} = \frac{4+3-1}{10} = \frac{6}{10} \)
Reduce la fracción dividiendo el numerador y el denominador por \( 2 \) y, por lo tanto,
\( \displaystyle \frac{2}{5} + \frac{3}{10} - \frac{1}{10} = \frac{3}{5} \)
b)
\( \displaystyle \frac{5}{9} \times \frac{3}{4} = \frac {5 \times 3}{9 \times 4} = \frac{15}{36}\)
Divide el numerador y el denominador por el MCD de \( 15 \) y \( 36 \) que es \( 3 \)
\( \displaystyle = \frac{15 \div 3}{36 \div 3} = \frac{5}{12}\)
c)
Para dividir una fracción por otra, multiplicamos la primera por el inverso de la segunda. Por lo tanto,
\( \displaystyle \frac{11}{2} \div \frac{1}{8} = \frac{11}{2} \times \frac{8}{1} = \frac{88}{2} = 44\)
d)
\( \displaystyle 4 \frac{3}{4} - 1 \frac{1}{2} = (4 - 1) + (\frac{3}{4} - \frac{1}{2}) \)
Convierte \( \displaystyle \frac{1}{2} \) a una fracción equivalente con denominador igual a \( 4 \) y sustituye
\( \displaystyle = 3 + (\frac{3}{4} - \frac{2}{4}) = 3 \frac{1}{4} \)
e)
Convierte el número mixto \( \displaystyle 6 \frac{3}{4} \) a una fracción
\( \displaystyle 6 \frac{3}{4} = 6 + \frac{3}{4} = \frac{24}{4} + \frac{3}{4} = \frac{27}{4} \)
La división se hace multiplicando por el inverso de \( 2 \). Por lo tanto,
\( \displaystyle \frac{27}{4} \times \frac{1}{2} = \frac{27}{8}\)
Convierte a un número mixto
\( \displaystyle \frac{27}{8} = \frac{24+3}{8} = 3 \frac{3}{8}\)
f)
Escribe \( 3 \) como fracción.
\( \displaystyle 3 = \frac{3}{1} \)
La división se convierte en una multiplicación por el inverso de \( \displaystyle \frac{3}{5} \). Por lo tanto,
\( \displaystyle 3 \div \frac{3}{5} = \frac{3}{1} \times \frac{5}{3} = 5 \)
g)
Convierte los números mixtos a fracciones impropias
\( \displaystyle 2 \frac{3}{5} = 2 + \frac{3}{5} = \frac{2}{1} + \frac{3}{5} = \frac{2 \times 5}{1 \times 5} + \frac{3}{5} = \frac{13}{5} \)
\( \displaystyle 3 \frac{3}{5} = 3 + \frac{3}{5} = \frac{3 \times 5}{1 \times 5} + \frac{3}{5} = \frac{18}{5} \)
Sustituye los números mixtos por las fracciones equivalentes encontradas anteriormente
\( \displaystyle 2 \frac{3}{5} \div 3 \frac{3}{5} = \frac{13}{5} \div \frac{18}{5} \)
Una división de fracciones se convierte en una multiplicación por el inverso.
\( \displaystyle 2 \frac{3}{5} \div 3 \frac{3}{5} = \frac{13}{5} \times \frac{5}{18} = \frac{13}{18} \)
a)
El número tiene el dígito \( 2 \) en las décimas. Por lo tanto,
\( 0.2 = \displaystyle \frac {2}{10} \)
Reduce las fracciones
\( = \displaystyle \frac {1}{5} \)
b)
El número tiene \(1 \) en las unidades, \( 2 \) en las décimas y \( 4 \) en las centésimas. Por lo tanto,
\( \displaystyle 1.24 = 1 + \frac{2}{10} + \frac{4}{100} = 1 + \frac{2 \times 10}{10 \times 10} + \frac{4}{100} = 1 \frac{24}{100} \)
Reduce la fracción
\( \displaystyle = 1 \frac{6}{25} \)
c)
\( \displaystyle 2.326 = 2 + \frac{3}{10} + \frac{2}{100} + \frac{6}{1000} = 2 \frac{163}{500} \)
Usa las reglas de división por \( 10 \), \( 100\), \( 1000 \), \( 10000 \), ...
a)
\( \displaystyle \frac{9}{100} = 0.09 \)
b)
\( \displaystyle \frac{17}{10000} = 0.0017\)
c)
\( \displaystyle 3 \frac{11}{100000} = 0.00011\)
a)
Convierte las fracciones al mismo denominador
\( \displaystyle \frac{2}{5} = \frac{8}{20} \)
\( \displaystyle \frac{3}{4} = \frac {15}{20} \)
Por lo tanto, la afirmación \( \displaystyle \frac{2}{5} \lt \frac{3}{4} \) es verdadera
b)
Convierte las fracciones al mismo denominador
\( \displaystyle \frac{1}{3} = \frac{10}{30} \)
\( \displaystyle \frac{3}{10} = \frac {9}{30} \)
Por lo tanto, la afirmación \( \displaystyle \frac{1}{3} \lt \frac{3}{10} \) NO es verdadera
5 - Exponentes
Soluciones
a)
\( 3 \times 3 \times 3 \times 3 = 3^4 \)
b)
\( 7 \times 4 \times 4 \times 4 \times 5 \times 5 = 7 \times (4 \times 4 \times 4 \times) \times (5 \times 5) = 7 \times 4^3 \times 5^2\)
a)
\( 2^4 = 2 \times 2 \times 2 \times 2 = 16 \)
b)
\( 3^2 \times 4^2 = (3 \times 3) \times (4 \times 4) = 9 \times 16 = 144\)
c)
Observa que \( 10^0 = 1 \), por lo tanto,
\( 10^0 \times 4^2 = 1 \times 4 \times 4 = 16 \)
6 - Razones, Tasas y Problemas Relacionados
Soluciones
a) triángulos a cuadrados : 4 a 7 b) cuadrados a triángulos : 7 a 4 c) cuadrados al total de figuras: 7:11
Escuela A: \( 1200 \) estudiantes , \( 400 \) niños , niñas \( 1200 - 400 = 800\), razón niñas a niños como fracción: \( \displaystyle \frac{800}{400} \) que se reduce a \( \displaystyle \frac{2}{1} \)
Escuela B: \( 800 \) estudiantes , \( 300 \) niños , niñas \( 800 - 300 = 500\), razón niñas a niños como fracción: \( \displaystyle \frac{500}{300} \) que se reduce a \( \displaystyle \frac{5}{3} \)
Compara las razones dadas por las fracciones y conviértelas a un denominador común
Escuela A: \( \displaystyle \frac{2}{1} = \frac{6}{3} \)
Escuela B: \( \displaystyle \frac{5}{3} \)
Comparando las razones dadas por las fracciones, la escuela A tiene una mayor proporción de niñas a niños.
Tasa unitaria: \( \displaystyle \frac{\$15}{5 \; \text{kg}} = 3 \; \$/\text{kg} \)
Tasa unitaria: \( \displaystyle \frac{350 \; \text{km}}{5 \; \text{hrs}} = 70 \; \text{km} / \text{hrs}\)
7 - Proporcionalidad y Problemas Relacionados
Soluciones
La distancia es proporcional al tiempo de la siguiente manera:
Distancia = velocidad × tiempo , la velocidad (o tasa) es constante
velocidad = \( \displaystyle \frac{240 \; \text{km}}{3 \; \text{hrs}} = 80 \; \text{km/hrs} \)
\( 400 \; \text{km} \) = velocidad × tiempo
tiempo = \( \displaystyle \frac{400 \; \text{km}}{80 \; \text{km/hrs} } = 5 \; \text{hrs}\)
Sea \( x \) la cantidad en dólares necesaria para comprar 320 dírhams.
Tasa de cambio: \( 4 \; \text{Dhs/\$} \) y es constante
\( 320 \; \text{Dhs} = x \times \; 4 \; \text{Dhs/\$}\)
\( x = \displaystyle \frac{320 \; \text{Dhs} }{4 \; \text{Dhs/\$}} = 80 \; \text{\$} \)
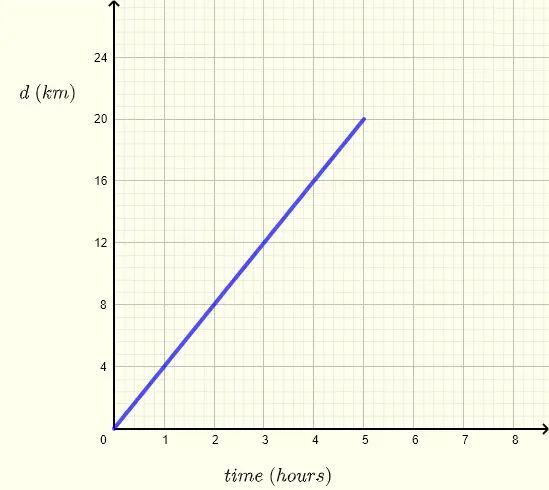
a)
Distancia = \( k \times\) tiempo
Del gráfico, en el tiempo \( 2 \) hrs la distancia \( d = 8 \) km
Por lo tanto,
\( 8 = k \times 2 \)
Calcula \( k \)
\( k = 8/2 = 4 \)
para el tiempo = 2.5 hrs;
d = \( 4 \times 2.5 = 10 \) km
b)
Es la constante \( k = 4 \) km/hrs
c)
Usando la fórmula Distancia = \( k \times \) tiempo, escribimos
\( 32 = 4 \times \) tiempo
El tiempo necesario para recorrer \( 32 \) km es \( 32 / 4 = 8 \) hrs,
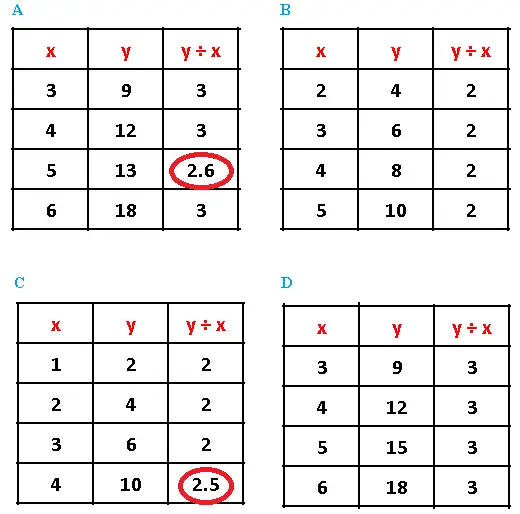
Para que \( y \) sea proporcional a \( x \), necesitamos tener la relación
\[ y = k x \]
donde \( k \) debe ser constante
La relación anterior también se puede escribir como
\[ \frac{y}{x} = k \]
A continuación se muestra la misma tabla completada por la razón \( y \div x \) a la derecha
Las razones \( y \div x \) en las tablas A) y C) NO son constantes (ver círculo rojo).
Sin embargo, las razones \( y \div x \) en las tablas B) y D) son constantes e iguales a \( 2 \) y \( 3 \) respectivamente.
Por lo tanto, \( y \) es proporcional a \( x \) en las tablas B) y D), pero no en A) y C)
8 - Porcentaje y Problemas Relacionados
Soluciones
\( \displaystyle 20\% \) de \( \displaystyle 10 = \frac{20}{100} \times 10 = \frac{200}{100} = 2 \)
\( 50\% \) de \( \displaystyle \frac{1}{4} = \frac{50}{100} \times \frac{1}{4} = \frac{50}{400} = \frac{1}{8} \)
Un porcentaje es una fracción con denominador igual a 100. Por lo tanto, para pasar de un denominador igual a \( 5 \) a un denominador igual a \( 100 \), multiplicamos por \( 20 \).
\( \displaystyle \frac {3}{5} = \frac {3 \times 20}{5 \times 20} = \frac{60}{100} = 60\% \)
Porcentaje de su salario mensual gastado en ropa = \( \displaystyle \frac {600}{3000} = \frac {600 \div 30}{3000 \div 30 } = \frac{20}{100} = 20\% \)
Cambio en porcentaje = \( \displaystyle \frac{100 - 120}{100} = \frac{-20}{100} = - 20 \% \)
Sea \( x \) el número tal que \( 10\% \) de \( x = 3 \)
\( 10\% \) de \( x = \displaystyle \frac {10}{100}\times x = \frac{10 x}{100} \)
Por lo tanto, la ecuación
\( \displaystyle \frac{10 x}{100} = 3 \)
Multiplica ambos lados de la ecuación por \( 100 \)
\( \displaystyle \frac{10 x}{100} \times 100= 3 \times 100 \)
Simplifica
\( 10 x = 300 \)
Resuelve para \(x \)
\( x = 30 \)
Después del aumento del 20%, el precio se vuelve
\( 40 + 20\% \times 40 = \$48 \)
Después de la disminución del 20% (del último precio) el precio final de la camisa es
\( 48 - 20\% \times 48 = 48 - 9.6 = \$38.4\)
9 - Convertir Unidades de Medida
Soluciones
Divide ambos lados de la igualdad dada \( 1 \text{ km} = 1000 \text{ m} \) por \( 1 \text{ km} \) para obtener un factor de conversión dado por
\[ \frac {1000 \text{ m}}{1 \text{ km}} = 1\]
Ahora escribimos que
\( 1.2 \text{ km} = 1.2 \text{ km} \times 1 \)
El factor de conversión encontrado anteriormente también es igual a 1 , por lo tanto, la sustitución
\[ \displaystyle 1.2 \text{ km} = 1.2 \text{ km} \times \frac {1000 \text{ m}}{1 \text{ km}} \]
Cancela \( \text{ km} \)
\[ \displaystyle 1.2 \text{ km} = 1.2 \cancel{\text{ km}} \times \frac {1000 \text{ m}}{1 \cancel{\text{ km}}} \]
Simplifica y evalúa
\[ 1.2 \text{ km} = 1200 \text{ m} \]
Divide ambos lados de la igualdad dada \( 1 \text{ galón estadounidense} = 3.78541 \text{ L} \) por \( 3.78541 \text{ L} \) para escribir el factor de conversión
\[ \displaystyle \frac{1 \text{ galón estadounidense}}{3.78541 \text{ L}} = 1 \]
Ahora escribimos
\[ 120 \text{ L} = 120 \text{ L} \times 1 \]
y sustituimos \( 1 \) por el factor de conversión que también es igual a \( 1 \)
\[ \displaystyle 120 \text{ L} = 120 \text{ L} \times \frac{1 \text{ galón estadounidense}}{3.78541 \text{ L}} \]
Cancela \( \text{ L} \)
\[ \displaystyle 120 \text{ L} = 120 \cancel{\text{ L}} \times \frac{1 \text{ galón estadounidense}}{3.78541 \cancel{\text{ L}}} \]
Simplifica y evalúa
\[ \displaystyle 120 \text{ L} = \frac{120 \times 1 \text{ galón estadounidense}}{3.78541 } = 31.70066 \text{ galones estadounidenses} \]
Observa que el símbolo \( m^2 \) que se lee como "metro cuadrado" se puede escribir como \( m^2 = m \times m\) y el símbolo \( ft^2 \) que se lee como "pies cuadrados" se puede escribir como \( ft^2 = ft \times ft\).
Multiplica ambos lados de la igualdad dada \( 1 \text{ m} = 3.28084 \text{ ft} \) por sí misma (elevar al cuadrado) para obtener
\[ (1 \text{ m})(1 \text{ m}) = (3.28084 \text{ ft})(3.28084 \text{ ft}) \]
Simplifica para obtener una igualdad con \( m^2 \) y \( ft^2 \)
\[ 1 \; m^2 = 10.76391 \; ft^2 \]
Divide ambos lados por \( 1 \; m^2 \) para obtener un factor de conversión dado por
\[ \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; m^2} = 1 \]
Escribe \( 0.3 \; m^2 \) como
\[ 0.3 \; m^2 = 0.3 \; m^2 \times 1 \]
Sustituye \( 1 \) por el factor de conversión que también es igual a \( 1 \)
\[ 0.3 \; m^2 = 0.3 \; m^2 \times \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; m^2} \]
Cancela \( m^2 \)
\[ 0.3 \; m^2 = 0.3 \; \cancel{m^2} \times \displaystyle \frac{ 10.76391 \; ft^2 }{1 \; \cancel{m^2}} \]
Simplifica y evalúa
\[ 0.3 \; m^2 = \displaystyle \frac{ 0.3 \times 10.76391 \; ft^2 }{1} = 3.229173 \; ft^2 \]
Dada la tasa \( 60 \) kilómetros por hora se puede escribir como
\[ \displaystyle \frac{60 \; km}{hr} \]
Convierte \( km \) a \( m \) y \( hr \) a minutos ( \(min\) ) usando el hecho de que \(1 km = 1000 \; m \) y \( 1 \; hr = 60 \; min \)
\[ \displaystyle \frac{60 \; km}{hr} = \frac{60 \times 1000 \; m }{60 \; min} \]
Simplifica
\[ \displaystyle \frac{60 \; km}{hr} = \frac{60 \times 1000 \; m}{60 \; min} = 1000 \; m/min\]
10 - Evaluar Expresiones
Soluciones
Expresión dada \( \; 2x - 2 \; \)
Sustituye \( x \) por \( -2 \) en la expresión dada
\[ 2 \times(-2) - 2 \]
Evalúa
\[ = -4 -2 = -6\]
Expresión dada \( \; | -5 + b | \; \)
Sustituye \( b \) por \( -10 \) en la expresión dada
\[ \; | -5 + (-10) | \; \]
Evalúa
\[ = | -5 -10 | = | -15 | = 15 \]
Expresión dada \( \; a - b \; \)
Sustituye \( a \) por \( -5 \) y \( b \) por \( -8 \) en la expresión dada
\[ \; -5 - (-8) = - 5 + 8 = 3 \; \]
11 - Álgebra
Soluciones
a)
Agrupa términos semejantes
\[ 3x - 2 + 4 x - 5 = (3x+4x) + (-2-5)\]
Simplifica
\[ = 7x + (-7) = 7 x - 7\]
b)
Expande los corchetes
\[ 3 (a + b + 2 ) + a + 4b - 12 = 3 a + 3 b + 6 + a + 4b - 12 \]
Agrupa términos semejantes
\[ = (3a + a) + (3b+4b) + (6-12) \]
Simplifica
\[ = 4 a + 7 b - 6\]
c)
\[ \displaystyle \frac{1}{3}( 6 x + 9) + 3 \]
Expande los corchetes
\[ = \displaystyle \frac{1}{3}( 6 x) + \frac{1}{3} (9) + 3 \]
Simplifica
\[ 2x + 3 + 3 = 2x + 6\]
d)
Usa el factorización para escribir la expresión dada de la siguiente manera
\[ 0.2 x + x = (0.2+1) x \]
Simplifica
\[ = 1.2 x \]
Factoriza las expresiones
a)
\( 14 x - 2 = \color{red}2 \times 7 x - \color{red}2 \times 1 = \color{red}2 (7x-1)\)
b)
\( 9 - 18 x = \color{red}9 \times 1 - \color{red}9 \times 2x = \color{red}9(1 - 2x)\)
c)
\( 4 b - 16 a + 4 = \color{red}4 \times b - \color{red}4 \times 4 a + \color{red}4 \times 1 = \color{red}4 (b - 4a +1) \)
12 - Ecuación con una Variable y Problemas Relacionados
Soluciones
a)
Dada la ecuación \( 3x - 2 = 4 \)
Suma \( 2 \) a ambos lados
\[ 3x - 2 + \color{red}2 = 4 + \color{red}2 \]
Simplifica
\[ 3x = 6\]
Divide ambos lados por \(3 \)
\[ \displaystyle \frac{3x}{3} = \frac{6}{3} \]
Simplifica
\[ x = 2 \]
b)
Dada la ecuación \( 9 - 3 = - x + 5 \)
Simplifica el lado izquierdo
\[ 6 = - x + 5 \]
Suma \( -5 \) a ambos lados
\[ 6 + \color{red}{-5} = - x + 5 + \color{red}{-5} \]
Simplifica
\[ 1 = - x \]
Multiplica ambos lados por \( -1 \)
\[ 1 (-1) = - x (-1) \]
Simplifica
\[ -1 = x \]
c)
Dada \( \displaystyle \frac{x}{3} = - 7 \)
Multiplica ambos lados por \( 3 \)
\[ \displaystyle \frac{x}{3} \times \color{red}{3} = - 7 \times \color{red}{3} \]
Simplifica
\[ x = - 21 \]
d)
Dada \( 4 \left(x + \displaystyle \frac{1}{4} \right) = -15\)
Expande los corchetes
\[ 4 x + 4 \times \displaystyle \frac{1}{4} = - 15 \]
Simplifica
\[ 4 x + 1 = - 15 \]
Resta \( -1 \) a ambos lados
\[ 4 x + 1 \color{red}{-1} = - 15 \color{red}{-1} \]
Simplifica
\[ 4 x = - 16 \]
Divide ambos lados por \( 4 \)
\[ \displaystyle \frac{4x}{4} = \frac{-16}{4} \]
Simplifica
\[ x = - 4 \]
e)
Dada \( \displaystyle \frac{x+2}{-3} = 3 \)
Multiplica ambos lados por \( -3 \)
\[ \displaystyle \frac{x+2}{-3} \times \color{red}{(-3)} = 3 \color{red}{(-3)} \]
Simplifica
\[ x + 2 = - 9 \]
Resta \( -2 \) a ambos lados y simplifica
\[ x = - 11 \]
f)
\( 2(x-1) = 3(x+2) \)
Expande los corchetes
\[ 2x - 2 = 3x + 6 \]
Resta \( -6 \) a ambos lados
\[ 2x - 2 + \color{red}{(-6 )} = 3x + 6 + \color{red}{(-6 )} \]
Simplifica
\[ 2x - 8 = 3x \]
Resta \( 2 x \) a ambos lados
\[ 2x - 8 \color{red}{-2x} = 3x \color{red}{-2x} \]
Simplifica
\[ - 8 = x \]
g)
Dada \(\displaystyle x - 2 \frac{1}{4} = 3 \)
Añade el número mixto \( 2 \frac{1}{4} \) a ambos lados
\[\displaystyle x - 2 \frac{1}{4} \color{red}{ + 2 \frac{1}{4}} = 3 \color{red}{ + 2 \frac{1}{4}} \]
Simplifica
\[\displaystyle x = 5 \frac{1}{4} \]
El perímetro de un jardín rectangular es de 340 m y su longitud es de 120 m. Sea \( x \) el ancho del jardín.
a)
Fórmula: Perímetro \( = 2 \times \text{longitud} + 2 \times \text{ancho} \)
Sustituye el perímetro por 340, la longitud por 120 y el ancho por \( x \)
\[ 340 = 2 \times 120 + 2 \times x \]
Simplifica
\[ 340 = 240 + 2 x \]
b)
Resuelve la ecuación en la parte a)
\[ x = 50 \]
c)
Verifica la respuesta
Perímetro = \( 2 \times \text{longitud} + 2 \times \text{ancho} \)
Sustituye la longitud y el ancho ( \( x = 50\) ) encontrados anteriormente
Perímetro = \[ 2 \times 120 + 2 \times 50 = 340 \]
como se da en el problema.
13 - Desigualdad con una Variable
Soluciones
Las tres desigualdades se representan en las rectas numéricas a continuación en rojo. Un círculo cerrado (rojo) significa que el valor está incluido. Un círculo abierto (rojo) significa que el valor está excluido
a), b) y c)
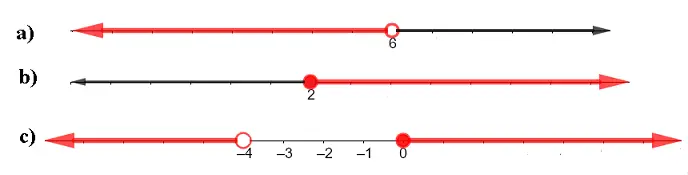
a) Dada \( 4x - 2 \gt 18 \)
Añade \( 2 \) a ambos lados de la desigualdad
\[ 4x - 2 \color{red}{+2} \gt 18 \color{red}{+2} \]
Simplifica
\[ 4x \gt 20 \]
Divide ambos lados por \( 4 \)
\[ \displaystyle \frac{4 x}{4} \gt \frac{20}{4} \]
Simplifica para obtener la solución de la desigualdad dada
\[ x \gt 5 \]
b)
\( 2(x + 3) \le 6 \)
Expande los corchetes en el lado izquierdo
\[ 2 x + 6 \le 6 \]
Resta \( 6 \) a ambos lados de la desigualdad
\[ 2 x + 6 \color{red}{-6} \le 6 \color{red}{-6} \]
Simplifica
\[ 2 x \le 0 \]
Divide ambos lados por \( 2 \)
\[ \displaystyle \frac{2 x}{2} \le \frac{0}{2} \]
Simplifica para obtener la solución de la desigualdad dada
\[ x \le 0 \]
14 - Figuras Bidimensionales
Soluciones
Se nos dan las medidas de dos ángulos; sea \( x \) la medida del tercer ángulo y la suma de los tres ángulos de un triángulo es igual a \( 180^{\circ} \), por lo tanto
\[ 36^{^{\circ}} + 54^{^{\circ}} + x = 180^{\circ} \]
Simplifica el lado izquierdo
\[ 90^{^{\circ}} + x = 180^{\circ} \]
Resuelve para \( x \) para obtener
\[ x = 90^{^{\circ}} \]
Por lo tanto, el triángulo dado es un triángulo rectángulo y b) es verdadero.
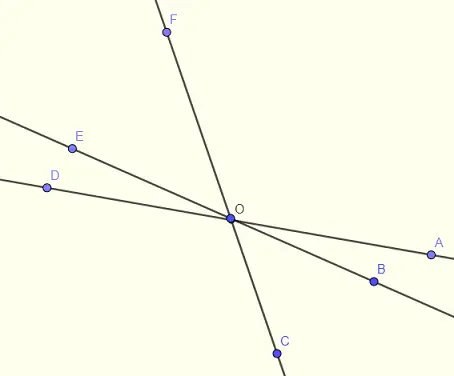
El ángulo \( \angle AOC \) es un ángulo recto y, por lo tanto, los ángulos \( \angle AOB \) y \( \angle COB \) son ángulos suplementarios y su suma es igual a \( 180^{\circ} \). Por lo tanto,
\[ \angle AOB + 27^{\circ} = 180^{\circ} \]
Resuelve para \( \angle AOB \) para obtener
\( \angle AOB = 153^{\circ} \)
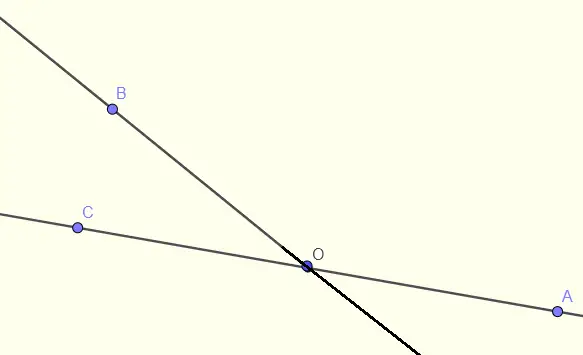
Lista de los pares de ángulos verticales en la figura de abajo:
\( \angle AOB \; \text{y} \; \angle DOE \quad \) , \( \angle BOC \; \text{y} \; \angle EOF \quad \) , \( \angle COD \; \text{y} \; \angle FOA \)
\( \angle FOB \; \text{y} \; \angle COE \quad \) , \( \angle AOC \; \text{y} \; \angle DOF \quad \) , \( \angle BOD \; \text{y} \; \angle EOA \)
a) Hexágono: 6 lados b) Pentágono: 5 lados c) Octágono: 8 lados
Un triángulo equilátero tiene 3 líneas de simetría como se muestra a continuación.
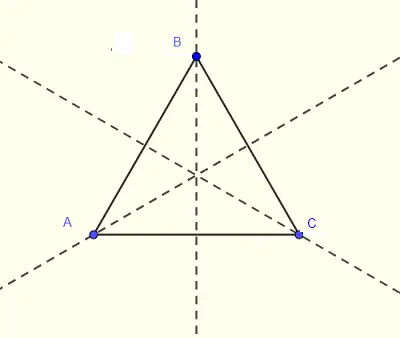
15 - Perímetro y Área de Figuras Planas
Soluciones
\( \text{radio} = \displaystyle \frac{\text{diámetro}}{ 2} = \frac{20 \; cm}{2} = 10 \; cm \)
\( \text{Área} = 3.14 \times \text{radio} \times \text{radio} = 3.14 \times 10 \times 10 = 314 \; cm^2\)
Perímetro del rectángulo = \( 2 \times \text{longitud} + 2 \times \text{ancho} \)
Sustituye la longitud y el ancho por los valores dados
Perímetro = \( 2 \times 10 + 2 \times 8 = 36 \text{ pulgadas} \)
Área del triángulo = \( \frac{1}{2} \times \text{altura} \times \text{base} \)
Sustituye la altura y la base por los valores dados
Área del triángulo = \( \frac{1}{2} \times 10 \times 5 = 25 \; cm^2 \)
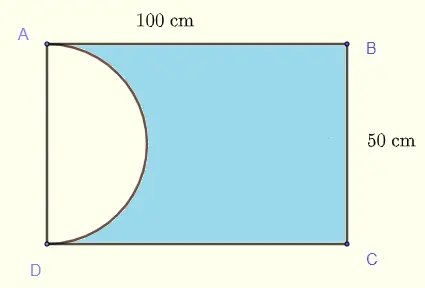
Para encontrar el área sombreada, resta el área de la semicircunferencia del área del rectángulo principal.
Área sombreada = área del rectángulo - área de la semicircunferencia
\( \text{El radio de la semicircunferencia = diámetro} / 2 = 50/2 = 25 \; cm \)
Área del rectángulo \( = \text{longitud} \times \text{ancho} = 100 \times 50 = 5000 cm^2 \)
Área de la semicircunferencia \( = \frac{1}{2} \times 3.14 \times \text{radio} \times \text{radio} = \frac{1}{2} \times 3.14 \times 25 \times 25 = 981.25 \; cm^2 \)
Área sombreada \( = 5000 \; cm^2 - 981.25 \; cm^2 = 4018.75 \; cm^2 \)
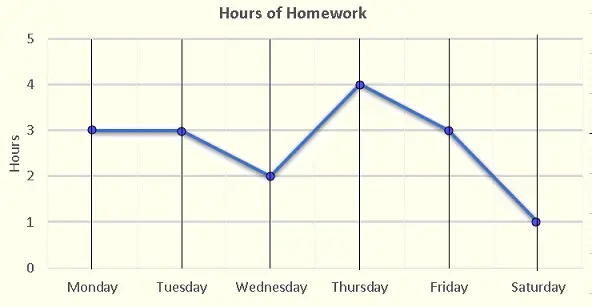
16 - Datos e Interpretación de Gráficos
Soluciones
a) Sábado
b) Jueves
c)
Número total de horas dedicadas a la tarea \( = 3 + 3 + 2 + 4 + 3 + 1 = 16 \; horas \)
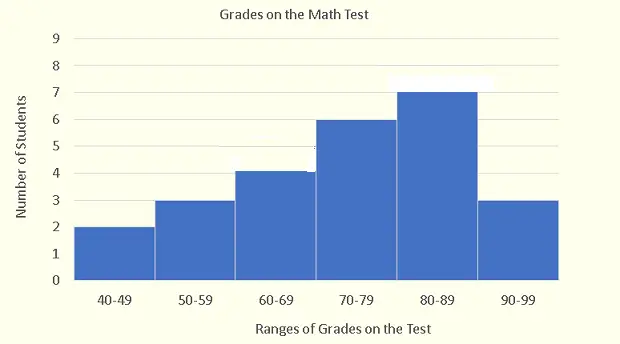
a) El número de estudiantes en esta clase se obtiene sumando el número de estudiantes (en el eje vertical) correspondiente a cada rango.
Número de estudiantes en esta clase \( = 2 + 3 + 4 + 6 + 7 + 3 = 25 \)
b)
De 70 a 89, tenemos dos rangos: de 70 a 79 con 6 estudiantes y de 80 a 89 con 7 estudiantes.
Hence \( 6 + 7 = 13 \) estudiantes obtuvieron entre 70 y 89 inclusive.
c)
El número de estudiantes que reprobaron son los rangos de 40 a 49 y 50 a 59 y el número de estudiantes en cada rango son 2 y 3 respectivamente. Por lo tanto,
El número de estudiantes que reprobaron \( = 2 + 3 = 5\)
El porcentaje del número total de estudiantes que reprobaron el examen \( = \frac{5}{25} = 20\% \)
17 - Estadísticas
Soluciones
Media \( = \displaystyle \frac{9 + 4 + 3 + 2 + 3 + 2 + 3 + 1 + 9}{9} = 4 \)
Ordena los datos dados de menor a mayor
\( \{ 1, 2, 2, 3, \color{red}3, 3, 4, 9, 9 \} \)
El valor de datos \( 3 \) tiene el mayor número de ocurrencias y, por lo tanto, es la moda
Hay 9 valores de datos y el valor de datos \( 3 \) (en rojo) está en el medio y, por lo tanto, es la mediana
Deja que \( x \) sea la puntuación del cuarto cuestionario de Joel. La media se da como 90, por lo tanto
Media \( = \displaystyle \frac{78+95+92+x}{4} = 90 \)
Simplifica y escríbelo como una ecuación
\( \displaystyle \frac{265+x}{4} = 90 \)
Multiplica ambos lados de la ecuación por \( 4 \)
\( \displaystyle \frac{265+x}{4} \times 4 = 90 \times 4 \)
Simplifica
\( 265 + x = 360 \)
Por lo tanto
\( x = 360 - 265 = 95 \)
Joel debería obtener 95 en su cuarto cuestionario para que el promedio de los 4 cuestionarios sea 90.
18 - Principio de Conteo
Soluciones
La cantidad de formas en que se puede servir el almuerzo en este restaurante es
\( 3 \times 5 \times 4 = 60 \)
El primer concesionario de automóviles tiene \( 3 \times 4 \times 3 = 36 \) opciones
El segundo concesionario de automóviles tiene \( 2 \times 5 \times 4 = 40 \) opciones
El segundo concesionario tiene más opciones.
19 - Probabilidades
Soluciones
Una medida de probabilidad toma valores entre 0 y 1 inclusive. Por lo tanto,
b) -0.5 y c) 2 no pueden ser medidas de probabilidades
Lanzar una moneda tiene 2 resultados: cara y cruz
Seleccionar una carta de cinco cartas diferentes tiene 5 resultados.
Usa el principio de conteo para encontrar el número de resultados cuando lanzas una moneda y seleccionas una de las cinco cartas al azar.
\( 2 \times 5 = 10 \) posibles resultados
a) El dado no tiene una cara con un cero y, por lo tanto, la probabilidad de obtener un cero es igual a cero.
b) Una cara de las 6 tiene un 5, la probabilidad es igual a 1/6
c) Las caras con 5 y 6 tienen números mayores que 4. Por lo tanto, dos caras de las 6 son mayores que 4, la probabilidad es igual a 2/6 = 1/3.
En este experimento, 5 estudiantes eligieron el azul como su color favorito y, por lo tanto, 15 eligieron un color favorito que no es azul.
Por lo tanto, si se encuesta a un estudiante, la probabilidad de que elija un color que no sea azul es igual a 15/20 = 3/4.
Más referencias y enlaces
- Temas de matemáticas de séptimo grado
- Preguntas y problemas de fracciones con soluciones