This is tutorial on finding the points of intersection of two ellipses given by their equations.
We first multiply all terms of the first equation by \( 16 \) and all the terms of the second equation by \( - 2 \) and simplify to obtain equivalent equations given by:
\( x^2 + 4 (y + 1)^2 = 16 \)
\( - x^2 - \dfrac{1}{6} (y + 2)^2 = - 2 \)
We now add side by side the two equations to obtain a quadratic equation
\( 4 (y + 1)^2 - \dfrac{1}{6} (y + 2)^2 = 14 \)
Multiply all terms by 6, group like terms and rewrite the equation as
\( 23 y^2 + 44y - 64 = 0 \)
Solve the quadratic equation for \( y \) to obtain two solutions
\( y \approx 0.97 \) and \( y \approx -2.88 \)
We now substitute the values of \( y \) already obtained into the equation \( x^2 + 4 (y + 1)^2 = 16 \)
and solve it for \( x \) to obtain the \( x \) values
for \( y \approx 0.97 \); \( x \) values are given by: \( x \approx 0.730365 \) and \( x \approx -0.730365 \)
for \( y \approx -2.88 \); \( x \) values are given by: \( x \approx 1.36788 \) and \( x \approx -1.36788 \)
The 4 points of intersection of the two ellipses are
\( ( 0.730365 , 0.97) \); \( ( -0.73 , 0.97) \); \( (1.37 , -2.88) \); \( (- 1.36788 , -2.88) \)
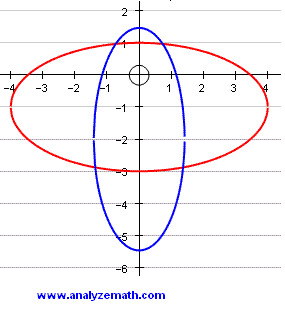
The graph of the two ellipses given above by their equations are shown below with their points of intersection.
