Solve right triangle problems including problems involving area, perimeter hypotenuse and sides and any relationship between them.
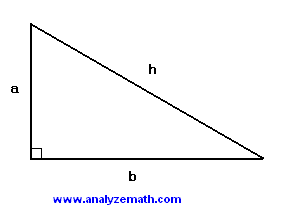
Any triangle with one of the angles equal to 90° is called a right angled triangle or simply a right triangle.
The area A of a right triangle with sides a and b is given by
A = (1 / 2) a × b
The perimeter P of a right triangle with sides a and b and hypotenuse h is given by
P = a + b + h
Using the Pythagorean theorem, we can write
h 2 = a 2 + b 2
which gives
h = √(a 2 + b 2)
Hence the perimeter can be written in terms of a and b only as follows:
P = a + b + √(a 2 + b 2)

Problem 1
Find the area and perimeter of a right angled triangle with sides of lengths 0.4 ft and 0.3 ft.
Solution to Problem 1
Let side a = 0.4, b = 0.3 and h being the hypotenuse.
Area = (1 / 2) a b = (1 / 2) 0.4 × 0.3 = 0.06 ft 2
Perimeter = a + b + h = a + b + √(a 2 + b 2)
= 0.4 + 0.3 + √(0.4 2 + 0.3 2) = 1.2 ft
Problem 2
Find the area and perimeter of an isosceles right angled triangle with hypotenuse of length 50 cm.
Solution to Problem 2
If a and b are the sides of the isosceles right angled triangle, then a = b
The Pythagorean theorem gives
a 2 + a 2 = 50 2
2 a 2 = 2500
a 2 = 1250
Area = (1 / 2) a 2 = (1/ 2) 1250 = 625 cm 2
Perimeter = 2 a + 50 = 2 √1250 + 50 = 50(√ 2 + 1) ≈ 120.7 cm
Problem 3
The first side of a right angled triangle is 200 m longer the second side. Its hypotenuse has a length of 1000 m. Find the lengths of the two sides, the area and the perimeter of this triangle.
Solution to Problem 3
Let the length of the second side be a = x.
The first side is 200 m longer the second side, hence it has a length b = x + 200
The hypotenuse h = 1000
Use the Pythagorean theorem to write
a 2 + b 2 = h 2
Substitute a, b and h by their algebraic expressions and/or values to write the equation
x 2 + (x + 200) 2 = 1000 2
Expand and simplify the terms in the above equation and write it in standard form
2 x 2 + 400 x - 960000 = 0
Solve to obtain two solutions
x = 600 and x = - 800
We select the positive solution x = 600 since x is a length.
The second side is a = x = 600 m
The first side is b = x + 200 = 800 m
Area = (1 / 2) a × b = (1/2) 600 × 800 = 240000 m 2
Perimeter = a + b + h = 600 + 800 + 1000 = 2400 m
Problem 4
A right angled triangle has one side that is 4/3 of the second. Its hypotenuse has a length of 30 ft. Find the sides, the area and the perimeter of this triangle.
Solution to Problem 4
Let the length of the second side be a = x.
The first side is 4/3 the second side, hence it has a length b = (4/3) x
The hypotenuse h = 30
Use the Pythagorean theorem to write
a 2 + b 2 = h 2
Substitute a, b and h by their values or algebraic expressions in the above equation.
x 2 + ( (4/3) x ) 2 = 30 2
Expand
x 2 + 16 x 2 / 9 = 900
Multiply all terms by 9 and simplify to eliminate the denominator
9 x 2 + 16 x 2 = 8100
25 x 2 = 8100
x 2 = 8100 / 25 = 324
x = √ 324 = 18
side a = x = 18 ft
side b = (4/3) x = 4 x / 3 = 4 × 18 / 3 = 24 ft
Area = (1 / 2) a × b = (1 / 2) × 18 × 24 = 216 ft 2
Perimeter = a + b + h = 18 + 24 + 30 = 72 ft
Problem 5
ABC is a right triangle with a perimeter equal to 60 units and an area is equal 150 units2. Find its two sides and hypotenuse.
Solution to Problem 5
The perimeter, the area and the Pythagorean theorem gives three equations as follows
Perimeter: a + b + h = 60
Area: (1 / 2) a b = 150 or a b = 300
Pythagorean Theorem: a 2 + b 2 = h 2
Rewrite the equation a + b + h = 60 as follows
a + b = 60 - h
Square both sides
(a + b)2 = (60 - h)2
Expand both sides
a2 + b2 + 2 a b = 602 + h2 - 120 h
Use the Pythagorean theorem
a 2 + b 2 = h 2
to substitute a 2 + b 2 by h 2 in the above equation to obtain
h2 + 2 a b = 602 + h2 - 120 h
Group like terms
2 a b = 602 - 120 h
A sustitution of (a b) by 300, since ab = 300, the above equation becomes
600 = 602 - 120 h
Solve for h to obtain
h = 25 units
Substitute h by 25 in the equation a + b + h = 60 to obtain
a + b = 60 - 25 = 35
Since a b = 300, then b = 300 / a which is substituted in the equation a + b = 35 to obtain
a + 300 / a - 35 = 0
Multiply all terms by a to obtain the quadratic equation
a 2 + 300 - 35 a = 0
Solve the above to obtain two solutions
a = 20 and a = 15
Use the equation a b = 300 to find b
when a = 20 , b = 15 and when a = 15 , b = 20
The lengths of the two sides of the right triangle are
15 units, 20 units
and the length of the hypotenuse is
25 units.
As an exercise check the perimeter and area given in the problem.
Problem 6
The right angled triangles shown below have angles ACB and DFE equal in size. The ratio of the hypotenuses AC and DF is AC / DF = 3 / 2. The area of triangle DEF is 100 unit2 . What is the area of triangle ABC?
