
Learn about similar triangles through definitions, theorems, worked examples, and practice problems with detailed step-by-step solutions.
Two triangles \( \triangle ABC \) and \( \triangle A'B'C' \) are similar if their corresponding angles are congruent and corresponding sides are proportional:
\[ \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{CA}{C'A'} \]

If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
Example 1:
Let \( \triangle ABC \) be a triangle and \( \overline{A'C'} \) parallel to \( \overline{AC} \). What can you say about \( \triangle ABC \) and \( \triangle A'BC' \)?

If corresponding sides of two triangles are proportional, the triangles are similar.
Example 2:
Given vertices \( A(-2,0), B(0,4), C(2,0) \) and \( P(-1,1), Q(0,3), R(1,1) \), show that \( \triangle ABC \sim \triangle PQR \).

If an angle of one triangle is congruent to an angle of another triangle, and the including sides are proportional, the triangles are similar.
Example 3:
Show that \( \triangle ABC \sim \triangle A'BC' \).

Problem 1:
In the diagram, \( \overline{A'C'} \parallel \overline{AC} \). Find length \( y = BC' \) and \( x = A'A \).

Problem 2:
A light source at \( L \) (height 2 m) shines through pole top \( P' \) to mountain top \( M' \). Pole height = 20 m. Distance mountain-pole = 1000 m, pole-laser = 10 m. Find mountain height \( h \).

Problem 3:
Given \( \triangle ABC \sim \triangle A'B'C' \) with ratio \( k \), find ratio \( \frac{BH}{B'H'} \) of their altitudes.

Problem 4:
Chords \( \overline{BA'} \) and \( \overline{AB'} \) intersect at \( C \). Find a relationship between segments \( AC, BC, B'C, A'C \).

Problem 5:
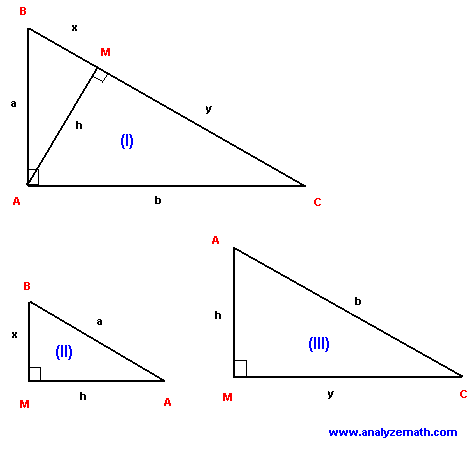
In right \( \triangle ABC \), \( \overline{AM} \perp \overline{BC} \). How many similar triangles are there?
Since \( \overline{A'C'} \parallel \overline{AC} \):
\( \angle BA'C' \cong \angle BAC \) (corresponding angles)
\( \angle BC'A' \cong \angle BCA \) (corresponding angles)
By AA similarity, \( \triangle ABC \sim \triangle A'BC' \).
Calculate side lengths:
\( AB = \sqrt{(0+2)^2 + (4-0)^2} = \sqrt{4 + 16} = 2\sqrt{5} \)
\( BC = \sqrt{(2-0)^2 + (0-4)^2} = \sqrt{4 + 16} = 2\sqrt{5} \)
\( CA = \sqrt{(-2-2)^2 + (0-0)^2} = 4 \)
\( PQ = \sqrt{(0+1)^2 + (3-1)^2} = \sqrt{1 + 4} = \sqrt{5} \)
\( QR = \sqrt{(1-0)^2 + (1-3)^2} = \sqrt{1 + 4} = \sqrt{5} \)
\( RP = \sqrt{(-1-1)^2 + (1-1)^2} = 2 \)
Ratios: \( \frac{AB}{PQ} = \frac{2\sqrt{5}}{\sqrt{5}} = 2 \), \( \frac{BC}{QR} = 2 \), \( \frac{CA}{RP} = 2 \)
Since \( \frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} \), by SSS similarity \( \triangle ABC \sim \triangle PQR \).
\( \angle ABC \cong \angle A'BC' \) (given)
Check including sides: \( \frac{BA}{BA'} = \frac{10}{4} = 2.5 \), \( \frac{BC}{BC'} = \frac{5}{2} = 2.5 \)
Since the ratios are equal and the included angles congruent, by SAS similarity \( \triangle ABC \sim \triangle A'BC' \).
Separate triangles: \( \triangle ABC \) and \( \triangle A'BC' \)
Since \( \overline{A'C'} \parallel \overline{AC} \), triangles are similar (AA).
Set up proportions: \( \frac{30 + x}{30} = \frac{22}{14} = \frac{y + 15}{y} \)
Solve for \( x \): \( \frac{30 + x}{30} = \frac{22}{14} \Rightarrow 14(30 + x) = 660 \)
\( 420 + 14x = 660 \Rightarrow 14x = 240 \Rightarrow x \approx 17.1 \)
Solve for \( y \): \( \frac{22}{14} = \frac{y + 15}{y} \Rightarrow 22y = 14y + 210 \)
\( 8y = 210 \Rightarrow y = 26.25 \)
Triangles \( \triangle LPP' \) and \( \triangle LMM' \) are similar (AA).
Proportions: \( \frac{LM}{LP} = \frac{MM'}{PP'} \Rightarrow \frac{1000 + 10}{10} = \frac{h - 2}{20 - 2} \)
\( \frac{1010}{10} = \frac{h - 2}{18} \Rightarrow 101 = \frac{h - 2}{18} \)
\( h - 2 = 1818 \Rightarrow h = 1820 \text{ meters} \).
Since triangles are similar, \( \angle B \cong \angle B' \) and \( \angle BAH \cong \angle B'A'H' \).
Right triangles \( \triangle BHA \) and \( \triangle B'H'A' \) are similar (AA).
Therefore: \( \frac{BH}{B'H'} = \frac{AB}{A'B'} = k \).
Join \( \overline{BA} \) and \( \overline{B'A'} \).
\( \angle ABA' \cong \angle AB'A' \) (subtend same arc)
\( \angle BAB' \cong \angle BA'B' \) (subtend same arc)
So \( \triangle ABC \sim \triangle A'B'C \) (AA).
Proportions: \( \frac{BC}{B'C} = \frac{CA}{CA'} \)
Cross multiply: \( BC \cdot CA' = B'C \cdot CA \).
Three similar triangles:
1. \( \triangle ABC \sim \triangle MBA \) (AA: right angle and \( \angle B \))
2. \( \triangle ABC \sim \triangle MAC \) (AA: right angle and \( \angle C \))
3. Consequently, \( \triangle MBA \sim \triangle MAC \).
Intercept Theorem and Problems
Geometry Tutorials and Problems
Congruent Triangles Examples