Overlapping circles area problems with detailed solutions.
The distance between the centers of two circles \( C_1 \) and \( C_2 \) is equal to 10 cm. The circles have equal radii of 10 cm. \( O \) is the center of \( C_2 \) and \( P \) is the center of \( C_1 \). Find the overlapping area of the two circles. Approximate your answer to one decimal place.
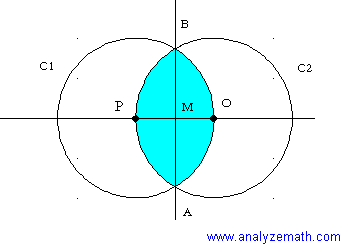
The overlapping area consists of two equal parts. We find one part (shown in blue below) and then multiply it by 2. Since the two circles have equal radii, \( M \) is the midpoint of segment \( OP \). Given \( OP = 10 \) cm, we find:
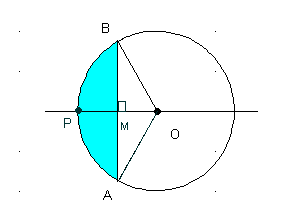
\[ d(O, M) = \frac{10}{2} = 5 \text{ cm} \] Using the cosine rule:
\[ \cos(\angle BOM) = \frac{d(O, M)}{OB} = \frac{5}{10} = \frac{1}{2} \]
Taking the arccos function:
\[ \angle BOM = 60^\circ \]
Since \( \angle AOB = 2 \times \angle BOM \):
\[ \angle AOB = 120^\circ \]
The area of the blue region is the difference between the area of sector \( OBPA \) and the area of triangle \( AOB \).
The area of sector \( OBPA \) is:
\[ \text{sector area} = \frac{1}{2} r^2 \theta \]
\[ = \frac{1}{2} (10)^2 \times \frac{120 \pi}{180} \]
\[ = \frac{100\pi}{3} \]
The area of triangle \( OBA \) is:
\[ \text{triangle area} = \frac{1}{2} r^2 \sin(120^\circ) \]
\[ = \frac{1}{2} (10)^2 \times \frac{\sqrt{3}}{2} \]
\[ = \frac{50\sqrt{3}}{2} \]
The blue region (Area 1) is:
\[ \text{Area 1} = \frac{100\pi}{3} - \frac{50\sqrt{3}}{2} \]
The total overlapping area (Area 2) is:
\[ \text{Area 2} = 2 \times \left( \frac{100\pi}{3} - \frac{50\sqrt{3}}{2} \right) \]
\[ \approx 122.8 \text{ cm}^2 \]