In this geometry problem, a triangle is tangent to a circle at two points. We are given specific lengths and must determine the radius of the circle using right triangle relationships and algebra.
Problem Statement
In the figure below, triangle \(ABC\) is tangent to a circle with center \(O\) at two points. The lengths are:
\[ AM = 6 \text{ cm}, \quad BC = 18 \text{ cm} \]Find the radius \(r\) of the circle.
Step-by-Step Solution
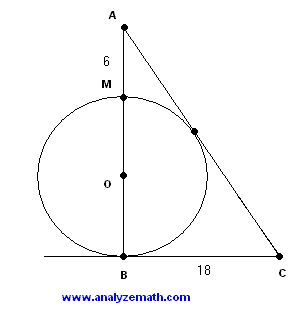
Let \(B\) and \(N\) be the points of tangency. Since a radius is perpendicular to the tangent at the point of tangency, several right triangles are formed.
Step 1: Apply the Pythagorean Theorem to Triangle \(AON\)
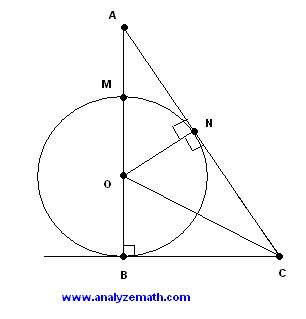
Let \(r\) be the radius of the circle. Then:
\[ AN^2 + r^2 = (r + 6)^2 \]Simplifying:
\[ AN^2 = 36 + 12r \implies AN = \sqrt{36 + 12r} \]Step 2: Use Congruent Right Triangles
Triangles \(ONC\) and \(OBC\) are right triangles with \(ON = OB = r\). Therefore, they are congruent and:
\[ NC = BC = 18 \]Step 3 & 4: Apply Pythagorean Theorem to Triangle \(ABC\) & Simplify
Expanding and simplifying yields:
\[ 4r^2 + 12r = 36AN \]Substitute \(AN = \sqrt{36 + 12r}\):
\[ r^2 + 3r = 9\sqrt{36 + 12r} \]Step 5 & 6: Square Both Sides and Solve the Equation
Square both sides:
\[ (r^2 + 3r)^2 = 81(36 + 12r) \]Expanding:
\[ r^4 + 6r^3 + 9r^2 - 972r - 2916 = 0 \]Solving the equation for the positive real solution valid for a radius:
\[ r = 9 \text{ cm} \]