Kite Questions with Solutions

Formulas, Properties, and Step-by-Step Solutions for Kite Geometry

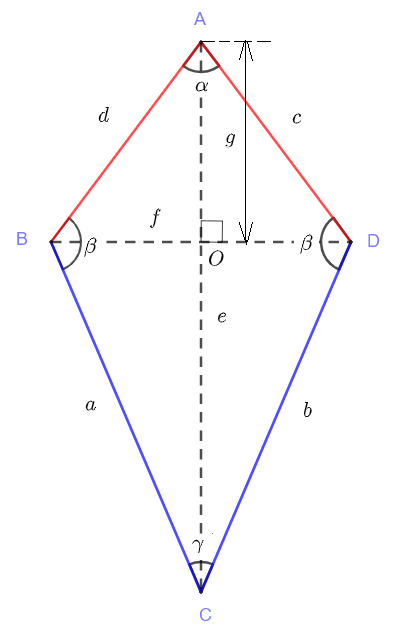
A kite is a quadrilateral with two pairs of adjacent sides equal in length. Formulas and comprehensive questions on kites are presented along with examples and detailed solutions.

Kite Formulas

In the diagram below, sides \(AB\) and \(AD\) have equal lengths, and sides \(CB\) and \(CD\) have equal lengths. The diagonal axis \(AC\) and the second diagonal \(BD\) intersect at an angle of \(90^\circ\).

kite diagram

We define the length of segments \(AC\), \(BD\), and \(AO\) using letters as follows: \(AC = e\), \(BD = f\), and \(AO = g\).
Note that: \(OC = AC - AO = e - g\) and \(BO = OD = \frac{f}{2}\).

  • Area \(A\) of Kite: \[ A = \dfrac{f \cdot e}{2} \]
  • Sides \(a\) and \(b\): \[ a = b = \sqrt{\left(\dfrac{f}{2}\right)^2 + (e - g)^2} \]
  • Sides \(c\) and \(d\): \[ d = c = \sqrt{\left(\dfrac{f}{2}\right)^2 + g^2} \]
  • Perimeter \(p\): \[ p = 2a + 2d \]
  • Angle \(\alpha\): \[ \alpha = 2 \arctan\left(\dfrac{f}{2g}\right) \]
  • Angle \(\gamma\): \[ \gamma = 2 \arctan\left(\dfrac{f}{2(e - g)}\right) \]
  • Angle \(\beta\): \[ \beta = 180^\circ - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} \]

A kite calculator is available and may be used to check answers to calculations.

Questions with Solutions

Question 1: Calculate sides, area, perimeter, and angles of a kite given diagonals and segment \(AO\)

Question: Calculate the sides \(a\) and \(d\), the area, the perimeter, and the angles \(\alpha\), \(\beta\), and \(\gamma\) of a kite with the diagonal axis of \(0.8\) meters, the second diagonal \(0.40\) meters, and distance \(AO\) of \(0.2\) meters.

Solution:

  • Given: \(e = 0.8\), \(f = 0.4\), and \(g = 0.2\)
  • Area: \[ A = \dfrac{f \cdot e}{2} = \dfrac{0.4 \cdot 0.8}{2} = 0.16 \, \text{square meters} \]
  • Side \(a\): \[ a = \sqrt{\left(\dfrac{f}{2}\right)^2 + (e - g)^2} = \sqrt{\left(\dfrac{0.4}{2}\right)^2 + (0.8 - 0.2)^2} \approx 0.63 \, \text{meters} \]
  • Side \(d\): \[ d = \sqrt{\left(\dfrac{f}{2}\right)^2 + g^2} = \sqrt{\left(\dfrac{0.4}{2}\right)^2 + 0.2^2} \approx 0.28 \, \text{meters} \]
  • Perimeter: \[ p = 2a + 2d = 2(0.63) + 2(0.28) = 1.82 \, \text{meters} \]
  • Angle \(\alpha\): \[ \alpha = 2 \arctan\left(\dfrac{f}{2g}\right) = 2 \arctan\left(\dfrac{0.4}{2 \cdot 0.2}\right) = 90^\circ \]
  • Angle \(\gamma\): \[ \gamma = 2 \arctan\left(\dfrac{f}{2(e - g)}\right) = 2 \arctan\left(\dfrac{0.4}{2(0.8 - 0.2)}\right) \approx 36.87^\circ \]
  • Angle \(\beta\): \[ \beta = 180^\circ - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} = 180^\circ - \dfrac{36.87^\circ}{2} - \dfrac{90^\circ}{2} \approx 116.57^\circ \]
Question 2: Calculate sides, angles, area, and perimeter given diagonals and angle \(\alpha\)

Question: Calculate the sides \(a\) and \(d\), the angles \(\beta\), \(\gamma\), the area, and the perimeter of a kite with the diagonal axis of \(e = 1.5\) meters, the second diagonal \(f = 0.50\) meters, and angle \(\alpha = 30^\circ\).

Solution:

  • Use triangle \(AOB\) to write: \(\sin(\alpha/2) = \dfrac{f/2}{d}\)
  • Solving for \(d\): \[ d = \dfrac{f/2}{\sin(\alpha/2)} = \dfrac{0.5/2}{\sin(15^\circ)} \approx 0.97 \, \text{meters} \]
  • Use triangle \(AOB\) to write: \(\tan(\alpha/2) = \dfrac{f/2}{OA}\)
  • Solving for \(g = OA\): \[ g = \dfrac{f/2}{\tan(\alpha/2)} = \dfrac{0.5/2}{\tan(15^\circ)} \approx 0.933 \, \text{meters} \]
  • Use triangle \(BOC\) to write: \(\tan(\gamma/2) = \dfrac{f/2}{e - g} = \dfrac{0.5/2}{1.5 - 0.933} \approx 0.44091\)
  • Solving for \(\gamma\): \[ \gamma = 2 \arctan(0.44091) \approx 47.59^\circ \]
  • Side \(a\): \[ a = \sqrt{(1.5 - 0.933)^2 + (0.5/2)^2} \approx 0.63 \, \text{meters} \]
  • Angle \(\beta\): \[ \beta = 180^\circ - \dfrac{\gamma}{2} - \dfrac{\alpha}{2} = 180^\circ - \dfrac{47.59^\circ}{2} - \dfrac{30^\circ}{2} \approx 141.21^\circ \]
  • Perimeter: \[ p = 2a + 2d = 2(0.63) + 2(0.97) \approx 3.2 \, \text{meters} \]
  • Area: \[ A = \dfrac{f \cdot e}{2} = \dfrac{0.5 \cdot 1.5}{2} = 0.375 \, \text{square meters} \]
Question 3: Find diagonal axis and angles given second diagonal and two interior angles

Question: Given the second diagonal \(f = 0.60\) meters and angles \(\alpha = 30^\circ\) and \(\beta = 120^\circ\), calculate the lengths of the diagonal axis \(AC = e\), the second diagonal \(BD = f\), and angle \(\gamma\).

Solution:

  • Use triangle \(AOB\) to write: \(\tan(\alpha/2) = \dfrac{f/2}{OA}\)
  • Solving for \(g = OA\): \[ g = \dfrac{f/2}{\tan(\alpha/2)} = \dfrac{0.60/2}{\tan(15^\circ)} \approx 1.12 \, \text{meters} \]
  • Use triangle \(ABC\) to write the sum of angles: \(\dfrac{\alpha}{2} + \dfrac{\gamma}{2} + \beta = 180^\circ\)
  • Solving for \(\gamma\): \[ \gamma = 2\left(180^\circ - \dfrac{\alpha}{2} - \beta\right) = 2\left(180^\circ - 15^\circ - 120^\circ\right) = 90^\circ \]
  • Use triangle \(BOC\) to write: \(\tan(\gamma/2) = \dfrac{BO}{OC}\)
  • Solving for \(OC = e - g\): \[ e - g = \dfrac{BO}{\tan(\gamma/2)} = \dfrac{0.6/2}{\tan(45^\circ)} = 0.3 \, \text{meters} \]
  • Therefore, diagonal axis \(e\): \[ e = 0.3 + g = 0.3 + 1.12 = 1.42 \, \text{meters} \]

More References and Links