Rhombus Geometry Problems

Rhombus problems with detailed solutions. Also see our Rhombus Calculator and Solver.

Definition and Properties

A rhombus is a parallelogram with four congruent sides. A square is a special case of a rhombus.

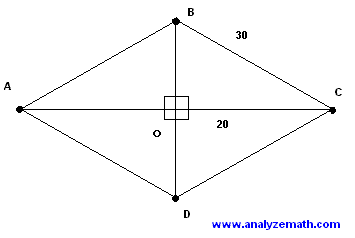
For rhombus \(ABCD\) above:

All sides are congruent: \(AB = BC = CD = DA = a\)
Opposite sides are parallel: \(AD \parallel BC\) and \(AB \parallel DC\)
Diagonals are perpendicular: \(AC \perp BD\)
Opposite angles are congruent: \(\angle A = \angle C\) and \(\angle B = \angle D\)
Consecutive angles are supplementary: \(\angle A + \angle B = 180^\circ\), \(\angle B + \angle C = 180^\circ\), \(\angle C + \angle D = 180^\circ\), \(\angle D + \angle A = 180^\circ\)

Area Formulas

Base × height: \(A = a \times h\)
Side and angle: \(A = a^2 \sin \theta\) (where \(\theta\) is any angle)
Diagonals: \(A = \frac{1}{2} d_1 d_2\)

Problems

Problem 1

The obtuse angle of a rhombus is twice its acute angle. The side length is 10 feet. Find the area.

Problem 2

The diagonals of a rhombus are 20 m and 48 m. Find the perimeter.

Problem 3

The perimeter of a rhombus is 120 feet and one diagonal is 40 feet. Find the area.

Solutions

Solution to Problem 1

Let \(x\) = acute angle, then \(2x\) = obtuse angle.
Since consecutive angles are supplementary:
\(x + 2x = 180^\circ\)
\(3x = 180^\circ\)
\(x = 60^\circ\)

Using area formula: \(A = a^2 \sin \theta\)
\(A = (10)^2 \sin 60^\circ = 100 \times \frac{\sqrt{3}}{2} \approx 86.6 \text{ ft}^2\)

Solution to Problem 2

Let diagonals \(d_1 = 20 \text{ m}\), \(d_2 = 48 \text{ m}\).
Diagonals bisect each other at right angles, so half-lengths are 10 m and 24 m.
Using Pythagorean theorem on one right triangle:
\(a^2 = 10^2 + 24^2 = 100 + 576 = 676\)
\(a = \sqrt{676} = 26 \text{ m}\) (side length)

Perimeter: \(P = 4a = 4 \times 26 = 104 \text{ m}\)

Solution to Problem 3

Perimeter = 120 ft ⇒ side length \(a = 120/4 = 30 \text{ ft}\).
One diagonal = 40 ft ⇒ half diagonal = 20 ft.
Using Pythagorean theorem:
\(30^2 = 20^2 + x^2\) where \(x\) = half of other diagonal
\(900 = 400 + x^2\)
\(x^2 = 500\)
\(x = \sqrt{500} = 10\sqrt{5} \text{ ft}\)

Full diagonal: \(d_2 = 2x = 20\sqrt{5} \text{ ft}\)
Area using diagonals: \(A = \frac{1}{2} d_1 d_2 = \frac{1}{2} \times 40 \times 20\sqrt{5} = 400\sqrt{5} \text{ ft}^2\)

Additional Resources

Geometry Tutorials and Problems
Rhombus Geometry Calculator