Graph of Sine, \( a \sin(bx+c) \), Function

Graphing and sketching sine functions of the form \[ f (x) = a \sin (bx + c) \] step by step tutorial is presented.

The properties such as domain, range and intercepts of the graphs of these functions are also looked at in detail.

Once you finish the present tutorial, you may want to go through a self test on trigonometric graphs. Free graph paper is available.

Review

We first start with the graph of the basic sine function \[ f (x) = \sin (x) \] The domain of function f is the set of all real numbers. The range of f is the interval \( [-1,1] \). \[ -1 \le sin (x) \le 1 \] Also function \( f(x) = \sin(x) \) is periodic with period equal to \( 2 \pi \) The graph of f over one period can be sketched by first finding points that give important information such as x intercepts, y intercept, maxima and minima. Let us make a table of values for function \( f \) over the interval one period: \( [0 , 2 \pi] \) \[ \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0 & \dfrac{\pi}{2} & \pi & \dfrac{3\pi}{2} & 2\pi \\ \hline f(x) & 0 & 1 & 0 & -1 & 0 \\ \hline \end{array} \] The choices of the values of \( x \) in the table correspond x and y intercepts, maxima; and minima points. These are useful points to graph the sine function over one period: \( [0 , 2 \pi] \).

To graph \( f \), we first graph the points in the table then join these points. Of course you may add extra points if you wish.

But the five points used are key points. Another important point to note is that the 5 key points divide the period into 4 equal parts. See figures below.

key points of sine function

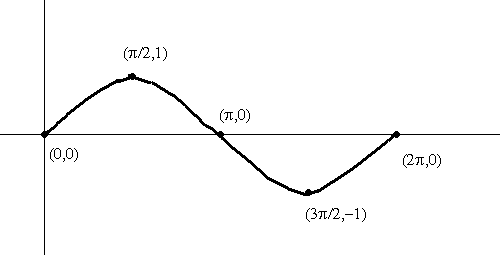
graph of sin(x)

To have a complete picture of why the graph of the sin(x) changes with x as shown above, you may want to go through an interactive tutorial on the trigonometric unit circle trigonometric unit circle.

Graphing \( f (x) = a \sin(b x + c) \)

We first need to understand how do the parameters \( a, b \) and \( c \) affect the graph of f (x)=a sin(bx+c) when compared to the graph of \( \sin(x) \) ? You may want to go through an interactive tutorial on sine functions. The domain of \( f \) is the set of all real numbers. The range of expression \( bx + c \) is the set of all real numbers. Therefore the range of \( \sin(b x + c) \) is \( [-1,1] \). Hence \[ -1 \le sin(bx+c) \le 1 \] Multiply both sides by a. If \( a \gt 0 \) then \[ -a \le a \sin(b x + c) \le a \] If \( a \lt 0 \) (change symbols of inequality) \[ -a \ge a \sin(b x + c) \ge a \] which may be written as \[ a \le a \sin(bx+c) \le - a \] We can say that parameter \( a \) affect the range of f which can be written as \[ [-|a| , |a|] \] \( | a | \) is called the amplitude of \( f \).

Period of f

Let us first assume that \( c = 0 \) and \( f (x) = a \sin (b x) \). For \( f \) to complete one cycle (period), expression \( b x \) needs to vary from \( 0 \) to \( 2\pi \) \[ 0 \leq bx \leq 2\pi \] Divide all terms in the inequality by \( b \).

If \( b > 0 \)

\[ 0 \leq x \leq \dfrac{2\pi}{b} \]

Period \( = \dfrac{2\pi}{b} - 0 = \dfrac{2\pi}{b} \)

If \( b < 0 \) (change symbols of inequalities)

\[ 0 \geq x \geq \dfrac{2\pi}{b} \]

Which is equivalent to

\[ \dfrac{2\pi}{b} \leq x \leq 0 \]

Period \( = 0 - \dfrac{2\pi}{b} = -\dfrac{2\pi}{b} \)

Using the absolute value notation, we can write the period of \( f \) as

\[ \text{Period} = \dfrac{2\pi}{|b|} \]

Phase Shift

We now consider the whole argument \( bx + c \). For \( f \) to complete one cycle (period), expression \( bx + c \) needs to vary from 0 to \( 2\pi \). \[ 0 \leq bx + c \leq 2\pi \] Assume \( b \gt 0 \) and solve for \( x \) \[ -c \leq bx \leq 2\pi - c \] Divide by \( b \) \[ \dfrac{-c}{b} \leq x \leq \dfrac{2\pi - c}{b} \] Period of \( f \) is given by: \[ \dfrac{2\pi - c}{b} - \dfrac{-c}{b} = \dfrac{2\pi}{|b|} \]. The constant \( c \) does not affect the period.

Let us now compare the cycle \([0 , \dfrac{2\pi}{b}]\) when \( c = 0 \) with the cycle \([ \dfrac{-c}{b} , \dfrac{2\pi - c}{b} ]\). This indicates that there is a shift of \( \dfrac{-c}{b} \). \[ \dfrac{-c}{b} \] is called the phase shift.

If \( \dfrac{-c}{b} \lt 0 \), the shift will be to the left.

If \( \dfrac{-c}{b} \gt 0 \), the shift will be to the right.

phase shift -c/b < 0

phase shift -c/b > 0

Example 1

f is a function given by \[ f (x) = 2 sin(3x - \pi/2 ] a - Find the domain of f and range of f.

b - Find the period and the phase shift of the graph of f.

c - Sketch the graph of function f over one period.

Solution to Example 1

a - The domain of f is the set of all real numbers .

The range is given by the interval \( [-2 , 2] \).

b - Period is: \[ \dfrac {2 \pi} {|b|} \] \[ = \dfrac {2 \pi} {3} \] Phase shift is : \[ - c / b = - (- \dfrac{\pi}{2}) / 3 \] \[= \dfrac{\pi}{6} \]

c - To sketch the graph of f over one period, we need to find the \( 5 \) key points first. Let \( 3x - \pi/2 \) vary from \( 0 to 2 \pi \) in order to have a complete period then find the values of \( f (x) \). See table below. \[ \begin{array}{|c|c|c|c|c|c|} \hline \textbf{\(3x - \dfrac{\pi}{2}\)} & 0 & \dfrac{\pi}{2} & \pi & \dfrac{3\pi}{2} & 2\pi \\ \hline \textbf{f(x)} & 0 & 2 & 0 & -2 & 0 \\ \hline \end{array} \]

We now need to find the corresponding values of \( x \). The first row in the table above gives \[ 0 \leq 3x - \dfrac{\pi}{2} \leq 2\pi \] Solve for \( x \) \[ \dfrac{\pi}{2} \leq 3x \leq 2\pi + \dfrac{\pi}{2} \] \[ \dfrac{\pi}{2} \leq 3x \leq \dfrac{5\pi}{2} \] \[ \dfrac{\pi}{6} \leq x \leq \dfrac{5\pi}{6} \] We now complete the table with the \( x \) values. Once the \( x \) values \( \dfrac{\pi}{6} \) and \( \dfrac{5\pi}{6} \), describing a whole period, are found, the other 3 points are found as follows:

The middle value is: \[ \left( \dfrac{\pi}{6} + \dfrac{5\pi}{6} \right) / 2 = \dfrac{3\pi}{6} \] Value at the first quarter: \[ \left( \dfrac{\pi}{6} + \dfrac{3\pi}{6} \right) / 2 = \dfrac{2\pi}{6} \] Value at the third quarter: \[ \left( \dfrac{3\pi}{6} + \dfrac{5\pi}{6} \right) / 2 = \dfrac{4\pi}{6} \] The fractions have not been reduced; this will make it easy to scale the \( x \)-axis in units of \( \dfrac{\pi}{6} \) and graph the points. \[ \begin{array}{|c|c|c|c|c|c|} \hline \textbf{3x - } \dfrac{\pi}{2} & 0 & \dfrac{\pi}{2} & \pi & \dfrac{3\pi}{2} & 2\pi \\ \hline f(x) & 0 & 2 & 0 & -2 & 0 \\ \hline x & \dfrac{\pi}{6} & \dfrac{2\pi}{6} & \dfrac{3\pi}{6} & \dfrac{4\pi}{6} & \dfrac{5\pi}{6} \\ \hline \end{array} \] We now draw the points given \( (x , f (x)) \) and join them by a smooth curve.

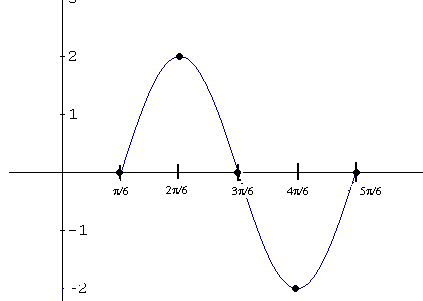
graph of f(x) = 2sin(3x-pi/2)

Matched Problem

\( f \) is a function given by \[ f (x) = (1/2)\sin(4x + \dfrac{\pi}{2} ) \] a - Find the domain of f and range of f.