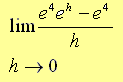 =
=
Solution
As h ----> 0
lim (e4 eh - e4) / h = (e4 e0 - e4) / 0
= 0 / 0 , indeterminate form
Another approach is needed. Let f(x) = ex. The given limit may be written as follows: as x ----> h
lim (e4 eh - e4) / h = lim (e4 + h - e4) / h = limit [ f(4+h) - f(4) ] / h
which is the definition of the first derivative of f(x) = ex at x = 4. Hence as x ---> h
lim (e4 eh - e4) / h = e 4
The graph of function g defined by

will have vertical asymptotes at
Solution
Let us first simplify, if possible, the given rational function
g(x) = (x3 + 2x2 - 3x) / (x2 + 2x - 3)
= x (x2 + 2x - 3) / (x2 + 2x - 3) = x
Function g has no vertical asymptotes
Given that

find

Solution
Using the theorem that states that the limit of a sum is equal to the sum of the limits. Hence as x ----> 0,
lim (x + 4x2 + sin x) / 3x = lim (x / 3x) + lim (4x2 / 3x) + (1/3) sin x / x
Simplify
= lim (1/3) + lim (4x) + (1/3) sin x / x
= 1/3 + 0 + (1/3)*1 = 2/3
Function f is defined by
 .
. Find df(x) / dx.
Solution
Using the theorem that states that the derivative of a sum of functions is the sum of the derivatives, we can write
d/dx [ 2x3sin(x) + (1/x)tan(x) + x sec(x) + 2 ]
= d/dx [ 2x3sin(x) ] + d/dx [ (1/x)tan(x) ] + d/dx [ x sec(x) ] + d/dx [ 2 ]
we now calculate the derivative of each term above
d/dx [ 2x3sin(x) ] = 2 [ 3x2 sin(x) + x3 cos(x) ] = 6x2 sin(x) + 2x3 cos(x)
d/dx [ (1/x)tan(x) ] = - (1/x2) tan(x) + (1/x) sec2(x))
d/dx [ x sec(x) ] = sec(x) + x sin(x) sec2(x)
d/dx [ 2 ] = 0
Hence
df/dx = 6x2 sin(x) + 2x3 cos(x) - (1/x2)tan(x) + (1/x sec2(x)) + sec(x) + x sin(x) sec2(x)
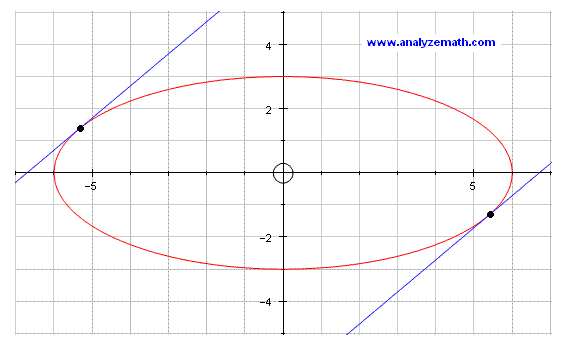
Curve C is described by the equation 0.25 x2 + y2 = 9. Determine the y coordinates of the points on curve C whose tangent lines have slope equal to 1.
Solution
Let us calculate the first derivative. Differentiate both sides of the given equation
0.25 (2x) + 2 y y ' = 0
y ' = - 0.5 x / (2 y)
We now solve the given equation 0.25 x2 + y2 = 9 for x
x = + or - sqrt [ (9 - y2) / 0.25 ]
Substitute x in y ' = - 0.5 x / (2 y) by + or - sqrt [ (9 - y2) / 0.25 ]
y ' = - 0.5 (+ or - sqrt [ (9 - y2) / 0.25 ] / (2 y)
The slope of the tangent is equal to 1. Hence
- 0.5 (+ or - sqrt [ (9 - y2) / 0.25 ] )/ (2 y) = 1
Solve the above for y. Two solutions
y = 3 sqrt(5) / 5 , y = - 3 sqrt(5) / 5
The graph of 0.25 x2 + y2 = 9 is shown below with the two tangent lines.
Find the solution to the differential equation dy/dx = cos(x) / y2 , where y(π/2) = 0.
Solution
The variable in the given differential equation may be separated as follows
y2 dy = cos(x) dx
Integrate both sides
∫ y2 dy = ∫ cos(x) dx
(1/3) y3 = sin(x) + C , constant of integration
We now use the condition y(π/2) = 0 to find the constant C
(1/3) y3(π/2) = sin(π/2) + C
0 = 1 + C
C = - 1
Substitute C by -1 in (1/3) y3 = sin(x) + C and solve for y
(1/3) y3 = sin(x) - 1
y3 = 3(sin(x) - 1)
y = (3 sin(x) - 3)1/3
Solution
Let u = cos x and therefore du/dx = - sin x. We now substitute cos x by u and sin x by -du/dx in the given integral. Hence
∫cos4(x)sin(x) dx = ∫ u4 (-du/dx) dx
= - ∫ u4du
= (-1/5)u5 + C , C constant of integration
= (-1/5)cos5(x) + C
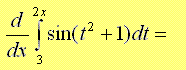
Solution
Let u = 2x and therefore du/dx = 2 or dx = du / 2. Hence the given integral becomes
d/dx ∫ 32xsin(t2 + 1) dt = 2 d/du ∫ 3usin(t2 + 1) dt
using the fundamental theorem of calculus, we obtain
= 2 sin(u2 + 1)
Substitute u by 2x
= 2 sin(4x2 + 1)
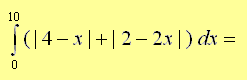
Solution
We first to analyze the signs of the expressions 4 - x and 2 - 2x between the limits of integration 0 and 10. 4 - x changes sign at x = 4 and 2 - 2x changes sign at x = 1.
for x between 0 and 4: 4 - x is positive and hence |4 - x| = 4 - x
for x between 4 and 10: 4 - x is negative and hence |4 - x| = -(4 - x)
for x between 0 and 1: 2 - 2x is positive and hence |2 - 2x| = 2 - 2x
for x between 1 and 10: 2 - 2x is negative and hence |2 - 2x| = -(2 - 2x)
We now rewrite the given integral as a sum of two integrals as follws.
∫ 010 (|4 - x|+|2 - 2x|) dx =
∫ 010 (|4 - x|) dx + ∫ 010 (|2 - 2x|) dx
We now calculate each of the individual integrals above as follows.
∫ 010 (|4 - x|) dx = ∫ 04 (4 - x) dx + ∫ 410 -(4 - x) dx = 8 + 18 = 26
and
∫ 010 (|2 - 2x|) dx = ∫ 01 (2 - 2x) dx + ∫ 110 -(2 - 2x) dx = 1 + 81 = 82
We now have
∫ 010 (|4 - x|) dx + ∫ 010 (|2 - 2x|) dx = 26 + 82 = 108
Evaluate the integral

Solution
Let u = 5 + x3/4 and therefore du/dx = (3/4) 1/x1/4 and substitute in the given integral
∫ (5 + x3/4)9 / (x1/4) dx = ∫ [ ( u9 ) / (x1/4) ] (4/3) x1/4 du
= (4/3) ∫ u9 du
= (4/3) (1/10) u10
= (2/15) (5 + x3/4)10
Given that function h is defined by
find h'(x).
Solution
Let u = arctan(x3 + 1) + 2x. Hence function h can be written as
h(x) = u4 h '(x) = 4 u3 u'
We now let v = arctan(x3 + 1) and calculate u '
u ' = (v ')( 1 / (1 + v2) )
= (3x2) / (1 + (x3 + 1)2)
= (3x2) / (x6 + 2x3 + 2)
Hence
h '(x) = 4 (arctan(x3 + 1) + 2x)3 (3x2) / (x6 + 2x3 + 2)
The graph of function h is shown below. How many zeros does the first derivative h' of h have?
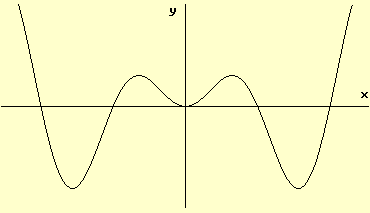
Solution
Whenever the graph of h has a local maximum or local minimum h '(x) is equal to 0. The given graph has 3 local minima and 2 local maxima and therefore h ' has 5 zeros.
The graph of a polynomial f is shown below. If f' is the first derivative of f, then the remainder of the division of f'(x) by x - b is more likely to be equal to

Solution
The graph of f has a local maximum at b and therefore f'(b) = 0. Since f is a polynomial then f ' is also a polynomial function such that f '(b) = 0 and according to the remainder theorem the division of f '(x) by x - b is equal to o.
The set of all points (ln(t - 2) , 3t), where t is a real number greater than 2, is the graph of
Solution
The given parametric equations may written as
x(t) = ln(t - 2) and y(t) = 3t
Solve y(t) = 3t for t
t = y / 3
Substitute t by y / 3 in x(t) = ln(t - 2)
x = ln(y / 3 - 2)
Solve for y
y/3 - 2 = ex y = 3 ( ex + 2 )
Let P(x) = 2 x3 + K x + 1. Find K if the remainder of the division of P(x) by x - 2 is equal to 10.
Solution
The Remainder theorem states that the division of P(x) by x - 2 is equal to P(2). Hence
P(2) = 2 (2)3 + K (2) + 1 = 10
Solve for K
K = - 7/2
Function f is defined by

where C is a constant. What must the value of C be equal to for function f to be continuous at x = 0?
Solution
For function f to be continuous at x = 0, lim f(x) as x approaches must be equal to f(0). We first find the limit of f(x) as x approaches 0. As x ---> 0,
lim [ sqrt(4x + 4) - sqrt(2x + 4) ] / 2x = 0 / 0 , indeterminate
Another approach is needed. Multiply numeartor and denominator by sqrt(4x + 4) - sqrt(2x + 4), simplify and find the limit. As x ---> 0,
lim [ sqrt(4x + 4) - sqrt(2x + 4) ] / 2x
= lim [ sqrt(4x + 4) - sqrt(2x + 4) ] [ sqrt(4x + 4) + sqrt(2x + 4) ]/ [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim [4x + 4 - 2x - 4] / [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim 2x / [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim 1 / [ sqrt(4x + 4) + sqrt(2x + 4) ]
= 1 / [ 2 + 2 ] = 1/4
In order for f to be continuous, we need to have
C = 1/4
f and g are functions such that f '(x) = g(x) and g '(x) = f(x). The second derivative of (f . g)(x) is equal to
A) f "(x) g "(x)
B) g '(x) g(x) + f(x) f '(x)
C) 4 g(x) f(x)
D) 2 g(x) f(x)
E) g(x) f(x)
Solution
First derivative of (f . g)(x)
(f . g) ' = f ' g + f g '
Second derivative of (f . g)(x)
(f . g) " = (f ' g + f g ') '
= f "g + f 'g' + f 'g' + f g" (I)
Note that since f '(x) = g(x) and g '(x) = f(x), we have
f " = g' and g " = f'
Substitute f " and g " in (I) above to obtain
(f . g) " = g 'g + f 'g' + f 'g' + f f'
We now substitute g ' by f and f ' by g to obtain
(f . g) " = fg + gf+ fg + f g = 4 fg
The average rate of change of the function f defined by f(x) = sin(x) + x on the closed interval [0 , pi] is equal to
Solution
The average rate of change of a function from a to b is defined by
(f(b) - f(a)) / (b - a)
Apply the above definition to the question above
(f(pi) - f(0)) / (pi - 0) = [ (sin(pi) + pi) - (sin(0)+ 0) ] / (pi - 0) = 1
The figure shows the graphs of y = sin(x) over half a period and the line y = 1/2. Find area of the shaded region.

Solution
The x coordinates of the points of intersection the line y = 1/2 and the graph of f are found by solving
sin(x) = 1/2 , for 0 ≤ x ≤ pi
solutions: x = pi / 6 and x = 5pi / 6
We first split the area to be calculated into 3 parts as shown below.
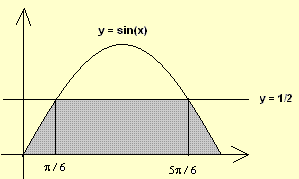
Calculate the area A adding the three parts (NOTING that the area in the middle is that of a rectangle):
A = ∫0pi/3 sin(x) dx+ 1/2(5Pi/6 - Pi/6) + ∫5pi/6pi sin(x) dx
= [ - cos(x) ]0pi/3 + pi / 3 + [- cos(x)]5pi/6pi
= 2 + pi / 3 - sqrt(3)
Functions f, g and h are defined as follow: g(x) = f(x2), f(x) = h(x3 + 1) and h'(x) = 2x + 1. g'(x) =
Solution
Let us express g(x) in terms of h
sin(x) = 1/2 , for 0 ≤ x ≤ pi
g(x) = f(x2) = h( (x2)3 + 1 )
= h(x6 + 1)
Let u = x6 + 1. Hence
g(x) = h(u) , with u = x6 + 1
Use chain rule to write
g '(x) = (du/dx) (dh/du)
If h'(x) = 2x + 1, then
dh/du = h '(u) = 2u + 1
Hence
g '(x) = 6x5 [ 2u + 1 ]
Substitute u by x6 + 1 in g '(x)
g '(x) = 6x5 [ 2(x6 + 1) + 1 ] =
= 12 x11 + 18 x5