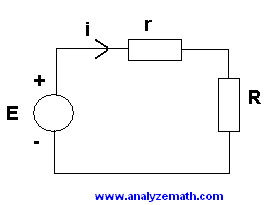
The first derivative is used to maximize (optimize) the power delivered to a load in electronic circuits.

Solution to the Problem
We first express power \(P\) in terms of \(E\), \(r\), and the variable \(R\) by substituting i = \(\dfrac{E}{(r + R)}\) into P = \(R i^2\).
\[ \text{P(R)} = \frac{R E^2}{(r + R)^2} \]
We now differentiate \(P\) with respect to the variable \(R\)
\[ \frac{dP}{dR} = \frac{E^2 [(r + R)^2 - R 2 (r + R)]}{[(r + R)^4]} = \frac{E^2 [(r + R) - 2 R]}{(r + R)^3} = \frac{E^2 (r - R)}{(r + R)^3} \]
To find out whether \(P\) has a local maximum, we need to find the critical points by setting \(\dfrac{dP}{dR} = 0\) and solve for \(R\).
Since \(r\) and \(R\) are both positive (resistances), \(\dfrac{dP}{dR}\) has only one critical point at \(R = r\). Also for \(R \lt r\), \(\dfrac{dP}{dR}\) is positive and \(P\) increases, and for \(R > r\), \(\dfrac{dP}{dR}\) is negative and \(P\) decreases. Hence \(P\) has a maximum value at \(R = r\). The maximum power is found by setting \(R = r\) in \(P(R)\)
\[ \text{P(r)} = \frac{r E^2}{(r + r)^2} = \frac{E^2}{4r} \]
So in order to have maximum power transfer from the electronic circuit to the load \(R\), the resistance of \(R\) has to be equal to \(r\).
As an example, the plot of \(P(R)\) for \(E = 5\) volts and \(r = 100\) Ohms is shown below and it clearly shows that \(P\) is maximum when \(R = 100\) Ohms = \(r\).
