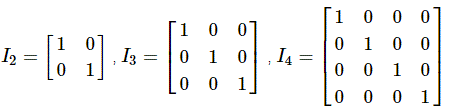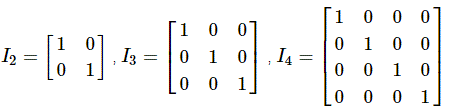逆矩阵问题及其解决方案 (Inverse Matrix Problems and Solutions)

教程包括示例和问题，以及有关如何求平方的倒数的详细解决方案矩阵采用行梯形法和辅因子法。讨论了逆矩阵的性质，并包含与逆矩阵相关的各种问题，包括一些具有挑战性的问题及其详细解决方案。

页面内容

单位矩阵的定义
矩阵逆的定义
使用行归约法求方阵的逆
使用次数、余因子和辅助求方阵的逆
2 x 2 矩阵的逆公式
逆矩阵的性质
关于逆矩阵的问题
问题解答
参考文献

定义单位矩阵 (Identity Matrix)

单位矩阵 I_n 是阶数为 n x n 的方阵，主对角线中的元素由 1 组成，所有其他元素都等于 0 。
单位矩阵的示例
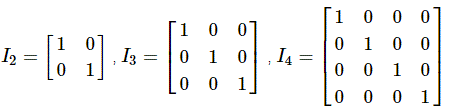
identity matrices

矩阵的逆矩阵的定义 (Definition of The Inverse of a Matrix)

令 A 为阶 n x n 的方阵。如果存在同阶矩阵 B 使得
A B = I _n = B A
其中 I _n 是阶 n x n 的单位矩阵，则 B 称为 A 的逆矩阵，矩阵 A 是 B 的逆矩阵。
示例1
验证下面给出的矩阵 A 和 B 互为逆矩阵。
2 by 2 Matrix for Example 1

解决办法
让我们找到产品AB和BA
Product of 2 by 2 Matrice for Example 1

AB = BA = I₂ 因此 A 和 B 互为逆。
方阵 A 的逆矩阵表示为 A^-1 并且是唯一的。

使用行缩减方法求方阵的逆 (Find the Inverse of a Square Matrix Using the Row Reduction Method)

这种方法也称为高斯-乔丹消去法。
我们首先写出增广矩阵 \( \) \( \) \( \) \( \) \[ [ A | I ] \] 其中 I 是与矩阵A同阶的单位矩阵，然后使用行初等运算将其重写为 \[ [ I | A^{-1} ] \] 其中 \( A^{-1} \) 是矩阵 A 的逆矩阵。
一个在线计算器包括使用行缩减找到矩阵的逆。

示例2
求矩阵 A 的逆矩阵： \[ A = \begin{bmatrix} 1&1 \\ 2&4 \end{bmatrix} \] 如果它存在。
解决办法
写出增广矩阵 \( [ A | I )\) \[ \begin{bmatrix} 1&1&|&1&0\\2&4&|&0&1 \end{bmatrix} \] 步骤1 \[ \color{red}{\begin{matrix} \\ R_2 - 2 \times R_1 \end{matrix} } \begin{bmatrix} 1&1&|&1&0\\0&2&|&-2&1 \end{bmatrix} \] 步骤 2 \[ \color{red}{\begin{matrix} \\ (1/2)R_2 \end{matrix} } \begin{bmatrix} 1&1&|&1&0\\0&1&|&-1&1/2 \end{bmatrix} \] 步骤 3 \[ \color{red}{\begin{matrix} R_1 - R_2 \\ \\ \end{matrix} } \begin{bmatrix} 1&0&|&2&-1/2\\0&1&|&-1&1/2 \end{bmatrix} \] A 的倒数是 2×2 右边的矩阵由下式给出 \[ A^{-1} = \begin{bmatrix} 2&-1/2\\-1&1/2 \end{bmatrix} \]

示例3
求矩阵 A 的逆矩阵，由下式给出
\[ A = \begin{bmatrix}-2&2&0 \\ 2&1&3\\ -2&4&-2\end{bmatrix} \] 如果它存在。
解决办法
写出增广矩阵 \( [ A | I )\) \[ \begin{bmatrix} -2&2&0&|&1&0&0\\ 2&1&3&|&0&1&0 \\ -2 & 4 & -2 &|& 0 & 0 & 1 \end{bmatrix} \] 步骤 1 \[ \color{red}{ \begin{matrix} \\ R_2 + R_1 \\ R_3 - R_1 \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 2 & -2 &|& -1 & 0 & 1 \end{bmatrix} \] 步骤 2 \[ \color{red}{ \begin{matrix} \\ \\ R_3 - (2/3) R_2 \\ \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 0 & - 4&|& -5/3 & -2/3 & 1 \end{bmatrix} \] 步骤 3 \[ \color{red}{ \begin{matrix} \\ \\ (-1/4)R_3 \\ \end{matrix}} \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] 步骤 4 \[ \color{red}{ \begin{matrix} \\ R_2 - 3\times R_3 \\ \\ \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&0&|&-1/4&1/2&3/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] 步骤 5 \[ \color{red}{ \begin{matrix} \\ (1/3) R_2 \\ \\ \end{matrix}} \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] 步骤 6 \[ \color{red}{ \begin{matrix} R_1- 2\times R_2 \\ \\ \\ \end{matrix} } \begin{bmatrix} -2&0&0&|&7/6&-1/3&-1/2\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] 步骤 7 \[ \color{red}{ \begin{matrix} (-1/2) R_1 \\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&0&|&-7/12&1/6&1/4\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] Hence \[ A^{-1} = \begin{bmatrix} -7/12&1/6&1/4\\ -1/12&1/6&1/4 \\ 5/12 & 1/6 & -1/4 \end{bmatrix} \]
有关如何使用行运算查找矩阵逆的更多示例包括在内。

使用辅因子和佐数求方阵的逆

使用数值示例来解释该方法。矩阵A如下所示。
\[ A = \begin{bmatrix} -1&0&1\\ 2&-1&2 \\ -1 & 2 & 1 \end{bmatrix} \] a) 求 A 的次要矩阵、辅因子矩阵、佐词矩阵和逆矩阵。
未成年人矩阵 (Matrix of Minors)
矩阵 A 的次数矩阵的条目 \( M_{i,j} \) 由删除 \( i^{th}\) 行和 \( j^{th}\) 所获得的行列式给出柱子。

要找到 \( M_{1,1} \)，请从矩阵 A 中删除第 1 行和第 1 列，然后找到剩余 2 x 2 矩阵的行列式，如下所示： \( M_{1,1} = Det \begin{bmatrix} .&.&.\\ .&-1&2 \\ .& 2 & 1 \end{bmatrix} = -1 - 4 = -5\)

要找到 \( M_{1,2} \)，请从矩阵 A 中删除第 1 行和第 2 列，然后找到剩余 2 x 2 矩阵的行列式，如下所示： \( M_{1,2} = Det \begin{bmatrix} .&.&.\\ 2&.&2 \\ -1 & . & 1 \end{bmatrix} = 2 -(-2) = 4 \)

要找到 \( M_{1,3} \)，请从矩阵 A 中删除第 1 行和第 3 列，然后找到剩余 2 x 2 矩阵的行列式，如下所示： \( M_{1,3} = Det \begin{bmatrix} .&.&.\\ 2&-1&. \\ -1 & 2 & . \end{bmatrix} = 4 - 1 = 3 \)

要找到 \( M_{2,1} \)，请从矩阵 A 中删除第 2 行和第 1 列，然后找到剩余 2 x 2 矩阵的行列式，如下所示： \( M_{2,1} = Det \begin{bmatrix} .&0&1\\ .&.&. \\ . & 2 & 1 \end{bmatrix} = 0 - 2 = - 2 \)
...
...
其余条目由下式给出： \( M_{2,2} = 0 \) , \( M_{2,3} = -2 \) , \( M_{3,1} = 1\) , \( M_{3,2} = -4\) , \( M_{3,3} = 1\).
未成年人 M 的矩阵由下式给出
\( M = \begin{bmatrix} -5&4&3\\ -2&0&-2\\ 1&-4&1 \end{bmatrix} \)
辅因子矩阵 (Matrix of Cofactors)
矩阵 A 的辅因子 C 矩阵的项 \( C_{i,j} \) 由下式给出 \( C_{i,j} = (-1)^{i+j}M{i,j} \)

对条目 \( C_{i,j} \) 的评估给出：
\( C_{1,1} = (-1)^{1+1} M_{1,1} = -5 \)
\( C_{1,2} = (-1)^{1+2} M_{1,2} = - 4 \)
\( C_{1,3} = (-1)^{1+3} M_{1,3} = 3 \)
\( C_{2,1} = (-1)^{2+1} M_{2,1} = 2 \)
\( C_{2,2} = (-1)^{2+2} M_{2,2} = 0 \)
\( C_{3,1} = (-1)^{3+1} M_{3,1} = 1 \)
\( C_{3,2} = (-1)^{3+2} M_{3,2} = 4 \)
\( C_{3,3} = (-1)^{3+3} M_{3,1} = 1 \)
因此，辅因子矩阵 C 由下式给出 \( C = \begin{bmatrix} -5&-4&3\\ 2&0&2\\ 1&4&1 \end{bmatrix} \)
矩阵的伴随（和伴随） (Adjugate (or adjunct) of a Matrix)
矩阵 A 的辅助（或辅助）是其辅因子 C 矩阵的转置。
\( Adjugate(A) = C^T = \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} \)
逆矩阵
我们现在需要找到矩阵 A 的行列式 D。
使用矩阵 A 的第一行和已找到的相应次要数，D 由下式给出：
\( D = det\begin{bmatrix} -1&0&1\\ 2&-1&2 \\ -1 & 2 & 1 \end{bmatrix} = A_{11}M_{1,1} - A_{1,2}M_{1,2} + A_{1,3}M_{1,3} = 8\)
矩阵 \( A \) 的逆矩阵由下式给出 \( A^{-1} = \dfrac{1}{D} C^T = \dfrac{1}{8} \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} = \begin{bmatrix} -\dfrac{5}{8}&\dfrac{1}{4}&\dfrac{1}{8}\\ -\dfrac{1}{2}&0&\dfrac{1}{2}\\ \dfrac{3}{8}&\dfrac{1}{4}&\dfrac{1}{8}\end{bmatrix}\)

2 × 2 矩阵的逆矩阵公式 (Formula for the Inverse of a 2 by 2 Matrix)

使用上述两种方法中的任何一种，都可以证明矩阵 A 的逆矩阵由下式给出： \[ A = \begin{bmatrix} a & b\\ c & d \\ \end{bmatrix} \] is given by \[ A^{-1} = \dfrac{1}{ad - bc}\begin{bmatrix} d & -b\\ -c & a \\ \end{bmatrix} \]

逆矩阵的性质 (Properties of Inverse Matrices)

具有逆矩阵的矩阵称为可逆矩阵。

如果 A 是可逆矩阵，则其逆矩阵唯一。
\( A A^{-1} = A^{-1} A = I \)
如果矩阵 A 和 B 可逆，则： \( (AB)^{-1} = B^{-1}A^{-1} \)
当且仅当其行列式不等于零时，矩阵才是可逆的。
行列式不等于零的矩阵称为非奇异矩阵。
\( (A^T)^{-1} = (A^{-1})^T \)
\( Det(A^{-1}) = \dfrac{1}{Det(A)} \)
\( (A^{-1})^{-1} = A \)

关于逆矩阵的问题 (Questions on Inverse Matrices)

问题1
使用行归约法求下列矩阵的逆矩阵：
\( A = \begin{bmatrix} -1&-1&1\\ 2&0&-2 \\ 1 & 1 & 1 \end{bmatrix} \) , \( B = \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \)
问题2
使用余因子方法求以下矩阵的逆矩阵。
\( A = \begin{bmatrix} -1&0&3\\ 3&2&2 \\ 0& 0 & 1 \end{bmatrix} \)
问题3
A、B 和 C 是 2 x 2 矩阵。矩阵 B 和 C 由下式给出：
\[ B = \begin{bmatrix} -1&-1\\ -2& 1 \end{bmatrix} , C = \begin{bmatrix} 2 & -1\\ -2 & 2 \end{bmatrix} \] 找到矩阵 A 使得 AB = C。
问题4
对于什么 k 值，下面给出的每个矩阵都是可逆的？
a) \( \begin{bmatrix} k & -1 & 4\\ 2 & 0 & 1\\ -1 & 0 & -1 \end{bmatrix} \) , b) \( \begin{bmatrix} k & -1 \\ -1 & 3 \end{bmatrix} \) , c) \( \begin{bmatrix} k & -1 & 4\\ 0 & k + 1 & 1\\ 0 & 0 & k -3 \end{bmatrix} \)
问题5
方阵 P、Q、R 和 S 具有相同维度且可逆，使得 \[ P = Q R^{-1} S \] 用\(P\)、\(Q\)和\(S\)或/和它们的矩阵逆来表达（或确定）\(R\)。
问题6
矩阵 A 由下式给出
\( A = \begin{bmatrix} a & 0 & 0 & 0\\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0\\ 0 & 0 & 0 & d \end{bmatrix} \)
如果参数 a、b、c 和 d 都不为零，则求矩阵 A 的逆矩阵公式。
问题7
使用逆矩阵来求解方程组 \( \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} = \begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} \)
问题8
求解下列方程组最有效的方法是什么？
\( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_i = B_i \)
问题9
A 和 B 是相同维数的可逆矩阵，关系式为： \( A^{-1} = A B \).
根据 A 或其逆来求 B。
问题10
1) 举一个 2 x 2 矩阵 A 和 B 不可逆的例子，但 A + B 是可逆的
2) 举一个 2 x 2 矩阵 A 和 B 不可逆的例子，但 A - B 是可逆的
问题11
使用这两种方法中的任何一种来找到 2 × 2 矩阵的逆公式。（上面已经给出了，但没有证明）。
问题12
矩阵形式的方程组
\( A X = B \)
有如下解决方案： \( X_1 = \begin{bmatrix} -1\\ 2 \\ 3 \end{bmatrix} \) for \( B_1 = \begin{bmatrix} 2\\ 13 \\ 3 \end{bmatrix} \) , \( X_2 = \begin{bmatrix} 0\\ -1 \\ 1 \end{bmatrix} \) for \( B_2 = \begin{bmatrix} 4\\ 2 \\ 2 \end{bmatrix} \) , \( X_3 = \begin{bmatrix} 1\\ 1 \\ 1 \end{bmatrix} \) for \( B_3 = \begin{bmatrix} 4\\ 5 \\ 3 \end{bmatrix} \).
查找 X 为 \( B = \begin{bmatrix} 1\\ -9 \\ -1 \end{bmatrix} \).

上述问题的解答

问题1的解答
矩阵 A 的逆矩阵
写出增广矩阵 \( [ A | I ] \) \[ \begin{bmatrix} -1&-1&1&|&1&0&0\\ 2&0&-2&|&0&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
步骤 1 \[ \color{red}{ \begin{matrix} -R_1\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 2&0&-2&|&0&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
步骤 2 \[ \color{red}{ \begin{matrix} \\ R_2-2R_1 \\ \\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&-2&0&|&2&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
步骤 3 \[ \color{red}{ \begin{matrix} \\ \\ R_3-R_1\\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&-2&0&|&2&1&0 \\ 0 & 0 & 2 &|& 1 & 0 & 1 \end{bmatrix} \]
步骤 4 \[ \color{red}{ \begin{matrix} \\ R_2=(-1/2)R_2\\ R_3=(1/2)R_3\\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
步骤 5 \[ \color{red}{ \begin{matrix} R_1+R_3\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&1&0&|&-1/2&0&1/2\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
步骤 6 \[ \color{red}{ \begin{matrix} R_1-R_2\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&0&|&1/2&1/2&1/2\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
矩阵 A 的逆矩阵是右侧的 3 x 3 矩阵。因此
\[ A^{-1} = \begin{bmatrix} 1/2&1/2&1/2\\ -1&-1/2&0 \\ 1/2 & 0 & 1/2 \end{bmatrix} \]

矩阵 B 的逆矩阵
写出增广矩阵 \( [ B | I ] \) \[ \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ -1& 1 & 2 & 0 &|&0&1&0&0 \\ -2& 0 & 1 & 2 &|& 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
步骤 1 \[ \color{red}{ \begin{matrix} \\ R_2+R_1\\ R_3+2R_1\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ 0& 1 & 3 & 2 &|&1&1&0&0 \\ 0& 0 & 3 & 6 &|& 2 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]

步骤 2 \[ \color{red}{ \begin{matrix} \\ \\ (1/3) R_3\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ 0& 1 & 3 & 2 &|&1&1&0&0 \\ 0& 0 & 1 & 2 &|& 2/3 & 0 & 1/3 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
步骤 3 \[ \color{red}{ \begin{matrix} R_1-2R_4\\ R_2-2R_4\\ R_3-2R_4\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&0 & |&1&0&0&-2\\ 0& 1 & 3 & 0 &|&1&1&0&-2 \\ 0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
步骤 4 \[ \color{red}{ \begin{matrix} R_1-R_3\\ R_2-3R_3\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&0 & |&1/3&0&-1/3&0\\ 0& 1 & 0 & 0 &|&-1&1&-1&4 \\ 0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
矩阵 B 的逆矩阵是右侧的 4 x 4 矩阵。因此
\[ B^{-1} = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \]
问题2的解答
我们首先找到未成年人。
\( M_{1,1} = Det \begin{bmatrix} .&.&.\\ .&2&2 \\ .& 0 & 1 \end{bmatrix} = 2\) , \( M_{1,2} = Det \begin{bmatrix} .&.&.\\ 3&.&2 \\ 0& . & 1 \end{bmatrix} = 3\) , \( M_{1,3} = Det \begin{bmatrix} .&.&.\\ 3&2&. \\ 0& 0 & . \end{bmatrix} = 0 \)

\( M_{2,1} = Det \begin{bmatrix} .&0&3\\ .&.&. \\ .& 0 & 1 \end{bmatrix} = 0\) , \( M_{2,2} = Det \begin{bmatrix} -1&.&3\\ . & . & . \\ 0& . & 1 \end{bmatrix} = -1\) , \( M_{2,3} = Det \begin{bmatrix} -1&0&.\\ . & . & .\\ 0& 0 & . \end{bmatrix} = 0\)

\( M_{3,1} = Det \begin{bmatrix} .&0&3\\ .&2&2 \\ . & . & . \end{bmatrix} = - 6\) , \( M_{3,2} = Det \begin{bmatrix} -1&.&3\\ 3&.&2 \\ . & . & . \end{bmatrix} = - 11\) , \( M_{3,3} = Det \begin{bmatrix} -1&0& .\\ 3&2& . \\ . & . & . \end{bmatrix} = - 2\)
辅因子矩阵 C 的条目定义为
\( C_{i,j} = (-1)^{i+j} M_{i,j} \) \[ C = \begin{bmatrix} 2&-3&0\\ 0&-1&0 \\ - 6 & 11 & -2 \end{bmatrix} \]
我们需要使用第三行找到 A 的行列式 D（它有 2 个零！）
\( D = A_{3,3} M_{3,3} = - 2 \)
矩阵 A 的逆矩阵由下式给出 \( A^{-1} = \dfrac{1}{D} C^T = -\dfrac{1}{2} \begin{bmatrix} 2&0&-6\\ -3&-1&11\\ 0&0&-2 \end{bmatrix} = \begin{bmatrix} -1&0&3\\ \dfrac{3}{2}& \dfrac{1}{2} & -\dfrac{11}{2}\\ 0&0&1\end{bmatrix}\)
问题3的解答
给定
\( A B = C \)
两边右乘以 \( B^{-1} \)
\( A B B^{-1} = C B^{-1}\)
在左侧使用关联性
\( A (B B^{-1}) = C B^{-1} \)
简化
\( A I = C B^{-1} \)
\( A = C B^{-1} \)
使用 2 x 2 矩阵的逆公式求出 B 的逆矩阵。
\( Det(B) = -3 \)
\( B^{-1} = - \dfrac{1}{3} \begin{bmatrix} 1&1\\ 2& -1 \end{bmatrix} \)

\( A = C B^{-1} = \begin{bmatrix} 2 & -1\\ -2 & 2 \end{bmatrix} (- \dfrac{1}{3}) \begin{bmatrix} 1&1\\ 2& -1 \end{bmatrix} = \begin{bmatrix} 0&-1\\ -2/3& 4/3 \end{bmatrix}\)

注意：您可以通过代入方程 \( A B = C \) 来检查矩阵 A 的答案
问题4的解答
如果矩阵的行列式不等于零，则该矩阵是可逆的。
a) 使用第二列，
Det\( \begin{bmatrix} k & -1 & 4\\ 2 & 0 & 1\\ -1 & 0 & -1 \end{bmatrix} = - 1\) 该矩阵对于任何 k 个实数都是可逆的

b) Det\( \begin{bmatrix} k & -1 \\ -1 & 3 \end{bmatrix} = 3k - 1\)
\( 3k - 1 \ne 0 \)
\( k \ne 1/3 \)
对于 k 不等于 1/3 的所有实数值，b) 部分中的矩阵是可逆的。

c) 给定矩阵是上三角矩阵，其行列式等于从左到右对角线中各项的乘积。
Det \( \begin{bmatrix} k & -1 & 4\\ 0 & k + 1 & 1\\ 0 & 0 & k -3 \end{bmatrix} k(k+1)(k-3)\)
\( k(k+1)(k-3) \ne 0 \)
如果 k 不等于 0、- 1 或 3，则给定矩阵可逆。
问题5的解答
将等式两边右乘以 \( S^{-1} \)
\( P S^{-1} = Q R^{-1} S S^{-1} \)
简化
\( P S^{-1} = Q R^{-1} I \)
\( P S^{-1} = Q R^{-1} \)
将等式两边左乘以 \( Q^{-1} \)
\( Q^{-1} P S^{-1} = Q^{-1} Q R^{-1} \)
简化
\( Q^{-1} P S^{-1} = I R^{-1}\)
\( Q^{-1} P S^{-1} = R^{-1} \)
两边取逆
\( (Q^{-1} P S^{-1})^{-1} = (R^{-1})^{-1} \)
简化
\( R = S P^{-1} Q \)
问题6的解答
写出增广矩阵 \( [ A | I ]\)

\( \begin{bmatrix} a & 0 & 0 & 0&|&1&0&0&0\\ 0 & b & 0 & 0&|&0&1&0&0 \\ 0 & 0 & c & 0 &|& 0 & 0 & 1 & 0\\ 0 & 0 & 0 & d &|& 0 & 0 & 0 & 1 \end{bmatrix} \)

将行 (1) 乘以 1/a、行 (2) 乘以 1/b、行 (3) 乘以 1/c、行 (4) 乘以 1/d 并化简

\( \begin{bmatrix} 1 & 0 & 0 & 0&|&1/a&0&0&0\\ 0 & 1 & 0 & 0&|&0&1/b&0&0 \\ 0 & 0 & 1 & 0 &|& 0 & 0 & 1/c & 0\\ 0 & 0 & 0 & 1 &|& 0 & 0 & 0 & 1/d \end{bmatrix} \)

给定矩阵的逆矩阵是

\( A^{-1} = \begin{bmatrix} 1/a&0&0&0\\ 0&1/b&0&0 \\ 0 & 0 & 1/c & 0\\ 0 & 0 & 0 & 1/d \end{bmatrix} \)
问题7的解答
该系统的形式为
A X = B with A = \( \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \) , \( B =\begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} \) and \( X = \begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} \)
将等式两边右乘以 \( A^{-1} \) 并化简。
\( A^{-1} A X = A^{-1} B \)
\( I_3 X = A^{-1} B , I_3 \) 是 3 x 3 单位矩阵
简化上面的
\( X = A^{-1} B \)
矩阵 A 的逆矩阵在问题 1 中计算，由下式给出（它是问题 1 中的矩阵 B）
\( A^{-1} = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \)
\( \begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} = A^{-1} B = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} = \begin{bmatrix}\dfrac{1}{3}\\ 10\\ -\dfrac{13}{3}\\ 2\end{bmatrix}\)
问题8的解答
由于矩阵 A 对于所有给定系统都是通用的，因此求解以下形式的方程组的最有效方法
\( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_2 = B_i \)
就是求矩阵A的逆并求解如下（见上面问题7）
\( X_1 = A^{-1} B_1 \) , \( X_2 = A^{-1} B_2 \) , \( X_3 = A^{-1} B_3 \) ... \( X_i = A^{-1} B_i \)

问题9的解答

问题10的解答
这个问题的两个部分都有很多可能的答案。
1) \(A = \begin{bmatrix} 1 & 1\\ 0 & 0 \\ \end{bmatrix} , B = \begin{bmatrix} 0 & 0\\ - 1 & 1 \\ \end{bmatrix} \) , \(A + B = \begin{bmatrix} 1 & 1\\ - 1 & 0 \\ \end{bmatrix} \)

2) \(A = \begin{bmatrix} 3 & 1\\ 0 & 0 \\ \end{bmatrix} , B = \begin{bmatrix} 0 & 0\\ - 1 & 4 \\ \end{bmatrix} \) , \(A - B = \begin{bmatrix} 3 & 1\\ 1 & - 4 \\ \end{bmatrix} \)
检查矩阵 A 和 B 的行列式是否等于 0，因此不可逆。检查 A + B 和 A - B 的行列式不等于 0，因此可逆。
问题11的解答
让 \(A = \begin{bmatrix} a & b\\ c & d \\ \end{bmatrix} \)
我们将使用辅因子的方法。我们首先计算未成年人
\( M_{1,1} = d\) , \( M_{1,2} = c\) , \( M_{2,1} = b\) , \( M_{2,2} = a\)
Then the cofactors using the formula: \( C_{i,j} = (-1)^{i+j}M_{i,j} \)
\( C_{1,1} = d\) , \( C_{1,2} = - c\) , \( C_{2,1} = - b\) , \( C_{2,2} = a\)
A 的行列式是
\( D = a d - b c \)
\( A^{-1} = \dfrac{1}{a d - b c} \begin{bmatrix} d & - c\\ - d & a \\ \end{bmatrix}^T = \dfrac{1}{a d - b c} \begin{bmatrix} d & - d\\ - c & a \\ \end{bmatrix} \)
问题12的解答
解可以写成矩阵形式如下
\( A \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix} \)
which gives
\( A = \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix} \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix}^{-1} \)
这给出了
\( A^{-1} = \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix}^{-1} \)
解 X 由下式给出
\( X = A^{-1} B = \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix}^{-1} \begin{bmatrix} 1\\ -9 \\ -1 \end{bmatrix} = \begin{bmatrix} 1\\ -2 \\ -1 \end{bmatrix} \)