Exponential Functions: Questions with Solutions
This page presents carefully selected questions on
exponential functions,
along with detailed, step-by-step solutions and clear explanations.
Properties of Exponential Functions
For all real numbers \(x\) and \(y\), and for any base \(a > 0\) with \(a \neq 1\):
-
\[
a^x a^y = a^{x+y}
\]
Example:
\[
2^3 \cdot 2^5 = 2^8
\]
-
\[
(a^x)^y = a^{xy}
\]
Example:
\[
(4^2)^5 = 4^{10}
\]
-
\[
(ab)^x = a^x b^x
\]
Example:
\[
(3 \times 7)^3 = 3^3 \cdot 7^3
\]
-
\[
\left(\frac{a}{b}\right)^x = \frac{a^x}{b^x}
\]
Example:
\[
\left(\frac{3}{5}\right)^3 = \frac{3^3}{5^3}
\]
-
\[
\frac{a^x}{a^y} = a^{x-y}
\]
Example:
\[
\frac{5^7}{5^4} = 5^3
\]
Questions with Detailed Solutions
Question 1
Simplify the following expression:
\[
2^x - 2^{x+1}
\]
Solution
-
Use the property \(a^{x+y} = a^x a^y\) to rewrite:
\[
2^{x+1} = 2^x \cdot 2
\]
-
Substitute:
\[
2^x - 2^x \cdot 2
\]
-
Factor out \(2^x\):
\[
2^x(1 - 2)
\]
-
Simplify:
\[
-2^x
\]
Question 2
Find constants \(A\) and \(k\) such that \(f(1)=1\) and \(f(2)=2\), where
\[
f(x) = A e^{kx}
\]
Solution
-
From \(f(1)=1\):
\[
A e^k = 1
\]
-
From \(f(2)=2\):
\[
A e^{2k} = 2
\]
-
Rewrite:
\[
A e^k e^k = 2
\]
-
Using \(A e^k = 1\):
\[
e^k = 2
\]
-
Take the natural logarithm:
\[
k = \ln(2)
\]
-
Substitute into \(A e^k = 1\):
\[
A = \frac{1}{2}
\]
-
Final form:
\[
f(x) = \frac{1}{2} e^{x\ln(2)} = 2^{x-1}
\]
Check:
\[
f(1) = 2^{0} = 1, \quad f(2) = 2^{1} = 2
\]
Question 3
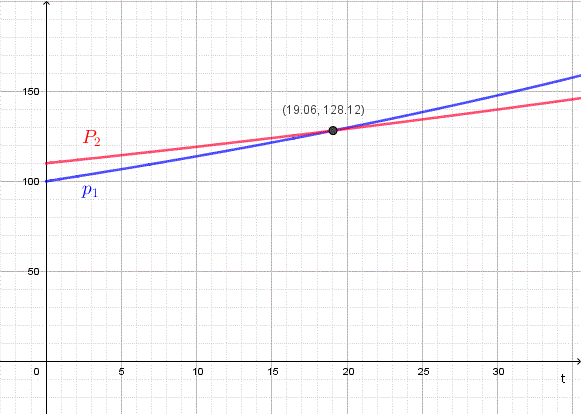
Two cities have populations (in thousands) given by:
\[
P_1(t) = 100 e^{0.013t}, \qquad
P_2(t) = 110 e^{0.008t}
\]
Here, \(t\) is time in years since 2004. When will the populations be equal,
and what will that population be?
Solution
-
Set \(P_1(t) = P_2(t)\):
\[
100 e^{0.013t} = 110 e^{0.008t}
\]
-
Divide by \(100 e^{0.008t}\):
\[
e^{0.005t} = 1.1
\]
-
Take the natural logarithm:
\[
0.005t = \ln(1.1)
\]
-
Solve:
\[
t = \frac{\ln(1.1)}{0.005} \approx 19
\]
-
Year:
\[
2004 + 19 = 2023
\]
-
Population:
\[
P_1(19) = 100 e^{0.013 \cdot 19} \approx 128
\]
thousand.
Graphical check:
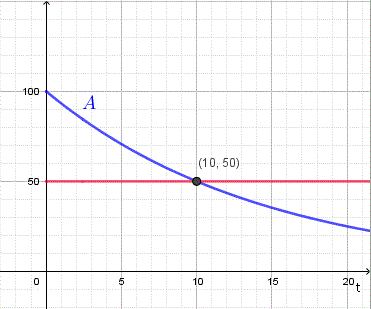
Question 4
A radioactive substance decays according to:
\[
A(t) = A_0 e^{rt}
\]
The half-life is 10 days. Find \(r\) to three decimal places.
Solution
-
At half-life:
\[
A_0 e^{10r} = \frac{A_0}{2}
\]
-
Simplify:
\[
e^{10r} = \frac{1}{2}
\]
-
Take ln:
\[
10r = \ln\left(\frac{1}{2}\right)
\]
-
Solve:
\[
r = 0.1 \ln\left(\frac{1}{2}\right) \approx -0.069
\]
More References

