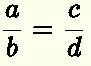We present examples on equivalent fractions and their solutions. More questions and their answers are included at the bottom of the page.
What are Equivalent Fractions?
Equivalent fractions represent the same part of the whole and may be written with different numerators and denominators.
The images below represent the same quantity in red: half of the whole. However, using fraction they may be written as:
image a):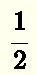
image b):
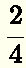image c):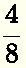
Because they represent the same quantity, we call them equivalent fractions and write that
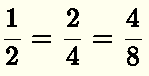
If two fractions
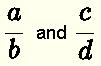are equivalent we write the following equality
\( \)\( \)\( \)
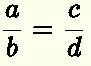
Multiply the left side and the right side by the product \( b \times d \)
\[ \color{red}{b \times d} \times \dfrac{a}{b} = \color{red}{b \times d} \times \dfrac{c}{d} \]
On the left side \( b \) is a common factor to the numerator and the denominator and may therefore be simplified. On the right side \( d \) is a common factor to the numerator and the denominator and may therefore be simplified. Hence we obtain the equality
\[ a \times d = b \times c \]
In general, equivalent fractions are written as
\[ \dfrac{a}{b} = \dfrac{c}{d} \quad\quad \text{ if and only if} \quad\quad a \times d = b \times c\]
The equality \( \quad a \times d = b \times c\) is called the cross product of the two fractions and may be used to check if two given fractions are equivalent.
The cross multiplication is symbolized by
\[ \displaystyle {\dfrac{a}{b} \color{red}{\rlap{\nearrow}{\searrow}} \dfrac{c}{d}} \]
Example 1
Which of the following pairs of fractions are equivalent?
a) \( \dfrac{2}{5} \) and \( \dfrac{3}{10} \)
b) \( \dfrac{3}{4} \) and \( \dfrac{12}{16} \)
c) \( \dfrac{5}{7} \) and \( \dfrac{3}{10} \)
d) \( \dfrac{2}{15} \) and \( \dfrac{14}{105} \)
e) \( \dfrac{-8}{7} \) and \( \dfrac{24}{-21} \)
Solution to Example 1
Apply the cross product rule given above
a)
\( \dfrac{2}{5} \rlap{\nearrow}{\searrow} \dfrac{3}{10} \)
\( 2 \times 10 \stackrel{?}{=} 5 \times 3 \)
simplify left and right sides
\( 20 \stackrel{?}{=} 15 \)
No, the two fractions are not equivalent.
b)
\( \dfrac{3}{4} \rlap{\nearrow}{\searrow} \dfrac{12}{16} \)
\( 3 \times 16 \stackrel{?}{=} 4 \times 12 \)
simplify
\( 48 \stackrel{?}{=} 48 \)
Yes, the two fractions are equivalent.
c)
\( \dfrac{5}{7} \rlap{\nearrow}{\searrow} \dfrac{3}{10} \)
\( 5 \times 10 \stackrel{?}{=} 7 \times 3 \)
simplify
\( 50 \stackrel{?}{=} 21 \)
The two fractions are not equivalent.
d)
\( \dfrac{2}{15} \rlap{\nearrow}{\searrow} \dfrac{14}{105} \)
\( 2 \times 105 \stackrel{?}{=} 15 \times 14 \)
simplify
\( 210 \stackrel{?}{=} 210 \)
Yes, the two fractions are equivalent.
e)
\( \dfrac{-8}{7} \rlap{\nearrow}{\searrow} \dfrac{24}{-21} \)
\( (-8) \times (-21) \stackrel{?}{=} 7 \times 24 \)
simplify
\( 168 \stackrel{?}{=} 168 \)
Yes, the two fractions are equivalent.
Example 2
Find the unknown given the following pairs of equivalent fractions
a) \( \dfrac{2}{5} \) = \( \dfrac{x}{10} \)
b) \( \dfrac{3}{y} \) = \( \dfrac{9}{15} \)
c) \( \dfrac{y}{-3} \) = \( \dfrac{6}{9} \)
d) \( \dfrac{14}{z} \) = \( \dfrac{-7}{2} \)
Solution to Example 2
Since the fractions are equivalent, we apply the cross product rule given above
a)
\( \dfrac{2}{5} \rlap{\nearrow}{\searrow} \dfrac{x}{10} \)
\( 2 \times 10 = 5 \times x \)
Simplify and solve for \( x \)
\( 20 = 5x \)
\( x = 20 / 5 = 4\)
b)
\( \dfrac{3}{y} \rlap{\nearrow}{\searrow} \dfrac{9}{15} \)
\( 3 \times 15 = y \times 9 \)
Simplify and solve for \( y \)
\( 45 = 9 y \)
\( y = 45 / 9 = 5\)
c)
\( \dfrac{y}{-3} \rlap{\nearrow}{\searrow} \dfrac{6}{9} \)
\( y \times 9 = (-3) \times 6 \)
Simplify and solve for \( y \)
\( 9y = -18 \)
\( y = -18 / 9 = -2\)
d)
\( \dfrac{14}{z} \rlap{\nearrow}{\searrow} \dfrac{-7}{2} \)
\( 14 \times 2 = z \times (-7) \)
Simplify and solve for \( y \)
\( 28 = - 7z \)
\( z = 28 / (-7) = - 4\)
Making Equivalent Fractions
You can make an equivalent fraction by dividing or multiplying both the numerator and denominator of the given fraction by the same integer number \( k \) not equal to ZERO:
\( \quad \quad \quad \dfrac{a}{b} = \dfrac{a \div k}{b \div k} \)
Example 3
Write an equivalent fraction, by multiplication, to each of the given fractions. There are many possible answers
a) \( \dfrac{3}{7} \)
b) \( \dfrac{2}{-9} \)
c) \( \dfrac{1}{5} \)
d) \( \dfrac{-3}{2} \)
e) \( \dfrac{-2}{-7} \)
Solution to Example 3
a)
Multiply numerator and denominator by any integer not equal to zero, \( 3 \) for example.
\( \dfrac{3}{7} = \dfrac{3 \times 3}{7 \times 3 } = \dfrac{9}{21} \)
b)
Multiply numerator and denominator by any integer not equal to zero, \( -2 \) for example.
\( \dfrac{2}{-9} = \dfrac{2 \times (-2) }{-9 \times (- 2) } = \dfrac{-4}{18} \)
c)
Multiply numerator and denominator by \( 5 \)
\( \dfrac{1}{5} = \dfrac{1}{5} = \dfrac{1 \times 5}{5 \times 5} = \dfrac{5}{25}\)
Example 4
Make an equivalent fraction, by division, to each of the given fractions.
a) \( \dfrac{8}{6} \)
b) \( \dfrac{3}{12} \)
c) \( \dfrac{-2}{10} \)
d) \( \dfrac{-3}{-9} \)
e) \( \dfrac{5}{-15} \)
Solution to Example 4
a)
Find the common factor of the numerator \( 8 \) and the denominator \( 6 \) which is \( 2 \), then divide the numerator and the denominator by this factor.
\( \dfrac{8}{6} = \dfrac{8 \div 2}{6 \div 2} = \dfrac{4}{3} \)
b)
Find the common factor of the numerator \( 3 \) and the denominator \( 12 \) which is \(3 \), then divide the numerator and the denominator by this factor.
\( \dfrac{3}{12} = \dfrac{3 \div 3 }{12 \div 3 } = \dfrac{1}{4} \)
c)
Find the common factor of the numerator \( -2 \) and the denominator \( 10 \) which is \( 2 \), then divide the numerator and the denominator by this factor.
\( \dfrac{-2}{10} = \dfrac{-2 \div 2}{10 \div 2} = \dfrac{-1}{5} \)
d)
Find the common factor of the numerator \( - 3 \) and the denominator \( - 9 \) which is \( 3 \) , then divide the numerator and the denominator by this factor.
\( \dfrac{-3}{-9} = \dfrac{-3 \div 3 }{-9 \div 3} = \dfrac{-1}{-3}\)
e)
Find the common factor of the numerator \( 5 \) and the denominator \( - 15 \) which is \( 5 \), then divide the numerator and the denominator by this factor.
\( \dfrac{5}{-15} = \dfrac{5 \div 5}{-15 \div 5} = \dfrac{1}{- 3} \)
Example 5
Given a fraction, find the one that is equivalent.
1) Given \( \dfrac{1}{3} \)
which of the following is equivalent to the given fraction?
a) \( \dfrac{2}{9} \) b) \( \dfrac{4}{15} \) c) \( \dfrac{3}{9} \) d) \( \dfrac{9}{3} \)
2) Given \( \dfrac{5}{9} \)
which of the following is equivalent to the given fraction?
a) \( \dfrac{9}{5} \) b) \( \dfrac{10}{27} \) c) \( \dfrac{-10}{18} \) d) \( \dfrac{10}{18} \)
3) Given \( \dfrac{-5}{7} \)
which of the following is equivalent to the given fraction?
a) \( \dfrac{15}{-21} \) b) \( \dfrac{-15}{14} \) c) \( \dfrac{10}{14} \) d) \( \dfrac{-4}{7} \)
4) Given \( \dfrac{-3}{-8} \)
which of the following is equivalent to the given fraction?
a) \( \dfrac{-3}{8} \) b) \( \dfrac{-6}{16} \) c) \( \dfrac{6}{-16} \) d) \( \dfrac{3}{8} \)
Solution to Example 5
One way to answer this question is to use the cross multiplication which we have already used in example 1. Another way, is to show that one fraction is obtained from the second by multiplication or division of the numerator and the denominator by the same integer.
1)
The given fraction \( \dfrac{1}{3} \) is equivalent to the fraction \( \dfrac{3}{9} \) in part c) because the cross product of the two fractions \( 1 \times 9 = 3 \times 3 \) produces a true statement after computation: \( 9 = 9 \)
Another way to explain that the fractions are equivalent: if both the numerator and the denominator of the given fraction \( \dfrac{1}{3} \) are multiplied by \( 3 \), we obtain \( \dfrac{3}{9} \).
2)
The given fraction \( \dfrac{5}{9} \) is equivalent to the fraction \( \dfrac{10}{18} \) in part d) because the cross product of the two fractions \( 5 \times 18 = 9 \times 10 \) produces a true statement after computation: \( 90 = 90 \).
If both the numerator and the denominator of the given fraction \( \dfrac{5}{9} \) are multiplied by \( 2 \), we obtain \( \dfrac{10}{18} \).
3)
The given fraction \( \dfrac{-5}{7} \) is equivalent to the fraction \( \dfrac{-15}{21} \) in part a) because the cross product of the two fractions \( -5 \times 21 = 7 \times (-15) \) produces a true statement after computation: \( -105 = -105 \)
If both the numerator and the denominator of the given fraction \( \dfrac{-5}{7} \) are multiplied by \( 3 \), we obtain \( \dfrac{-15}{21} \).
4)
The given fraction \( \dfrac{-3}{-8} \) is equivalent to the fraction \( \dfrac{3}{8} \) in part d) because the cross product of the two fractions \( - 3 \times 8 = -8 \times 3 \) produces a true statement after computation: \( -24 = -24 \)
If both the numerator and the denominator of the given fraction \( \dfrac{-3}{-8} \) are multiplied by \( -1 \), we obtain \( \dfrac{3}{8} \).
Questions
Which of the following pairs of fractions are equivalent?
\( \dfrac{1}{10} \) and \( \dfrac{2}{20} \)
\( \dfrac{7}{3} \) and \( \dfrac{14}{8} \)
\( \dfrac{2}{7} \) and \( \dfrac{10}{70} \)
\( \dfrac{3}{15} \) and \( \dfrac{1}{15} \)
\( \dfrac{9}{17} \) and \( \dfrac{18}{34} \)
Find the unknown given the following pairs of equivalent fractions
\( \dfrac{1}{4} \) = \( \dfrac{x}{16} \)
\( \dfrac{7}{y} \) = \( \dfrac{-21}{15} \)
\( \dfrac{y}{-6} \) = \( \dfrac{6}{9} \)
\( \dfrac{3}{z} \) = \( \dfrac{15}{75} \)
Answers to the Above Questions
\( \dfrac{1}{10} = \dfrac{2}{20} \)
\( \dfrac{7}{3} \ne \dfrac{14}{8} \)
\( \dfrac{2}{7} \ne \dfrac{10}{70} \)
\( \dfrac{3}{15} \ne \dfrac{1}{15} \)
\( \dfrac{9}{17} = \dfrac{18}{34} \)
Find the unknown given the following pairs of equivalent fractions
image b): 
image c): 
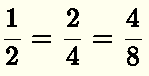
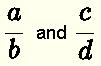are equivalent we write the following equality
