Équation d'un cercle
Contenu de la page
Équation d'un cercle sous forme standard
Un cercle de centre C donné par ses coordonnées C(h,k) est illustré ci-dessous. Par définition, tous les points M(x,y) du cercle sont à égale distance du centre. En d'autres termes, un cercle de centre C est l'ensemble de tous les points qui sont à égale distance du point C . Cette distance entre C et n'importe quel point du cercle est appelée rayon et a une longueur r dans le graphique ci-dessous.

La distance du centre C(h,k) à un point M(x,y) sur le cercle est donnée par
 Pour trouver l'équation, on utilise la définition pour écrire que la distance CM est égale au rayon r
Pour trouver l'équation, on utilise la définition pour écrire que la distance CM est égale au rayon r
 Travailler avec la racine carrée ajoute des difficultés supplémentaires qui peuvent être évitées. La racine carrée de l'équation ci-dessus peut être éliminée en mettant au carré les deux côtés de l'équation pour obtenir
Travailler avec la racine carrée ajoute des difficultés supplémentaires qui peuvent être évitées. La racine carrée de l'équation ci-dessus peut être éliminée en mettant au carré les deux côtés de l'équation pour obtenir
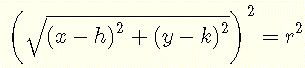 Simplifiez pour obtenir l'équation standard d'un cercle de centre C(h,k) et de rayon r
Simplifiez pour obtenir l'équation standard d'un cercle de centre C(h,k) et de rayon r
\( \) \( \) \( \) \( \)
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Exemples
Exemple 1
Trouver l'équation standard du cercle de centre C(2,5) et de rayon r = 2
Solution de l'exemple 1
Étant donné le centre et le rayon, l’équation standard du cercle est donnée par :
\( (x - 2)^2 + (y - 5)^2 = 2^2 \)
Points sur, à l'intérieur ou à l'extérieur d'un cercle
Pour savoir si un point donné se trouve sur un cercle, à l'intérieur d'un cercle ou à l'extérieur d'un cercle, on compare le carré de la distance du centre du cercle au point donné au carré du rayon. On utilise le carré de la distance au lieu de la distance pour éviter d'utiliser la racine carrée.
Pour un cercle de centre \( C(h,k) \) et de rayon \( r \), point \( P \) de coordonnées \( (x_0 , y_0) \)
1) est sur le cercle, si l'égalité suivante est satisfaite :
\[ (x_0 - h)^2 + (y_0 - k)^2 = r^2 \]
2) est à l’intérieur du cercle, si l’inégalité suivante est satisfaite :
\[ (x_0 - h)^2 + (y_0 - k)^2 \lt r^2 \]
3) est en dehors du cercle, si l’inégalité suivante est satisfaite :
\[ (x_0 - h)^2 + (y_0 - k)^2 \gt r^2 \]
Exemple 2
Equation d'un cercle et de points à l'intérieur, à l'extérieur ou sur le cercle
Lequel des points suivants \( P_1(1,5) \) , \( P_2(2,3) \) et \( P_3(4,7) \) se trouve à l'intérieur, à l'extérieur ou sur le cercle donné dans l'exemple 1 ?
Solution de l'exemple 2
Le centre du cercle dans l'exemple 1 est à \( C(2,5) \) et a un rayon \( r = 2 \)
Trouvez le carré de la distance entre le centre du cercle et chacun des points donnés et comparez-le au carré du rayon
le carré de la distance de \( C \) à \( P_1 \) est donné par : \( (2-1)^2 + (5-5)^2 = 1\) qui est plus petit que \( r^2 = 4\). Donc le point \( P_1 \) est à l’intérieur du cercle.
le carré de distance de \( C \) à \( P_2 \) est donné par : \( (2-2)^2 + (5-3)^2 = 4\) qui est égal à \( r^2 = 4\). Donc le point \( P_1 \) est sur le cercle.
le carré de la distance de \( C \) à \( P_3 \) est donné par : \( (2-4)^2 + (5-7)^2 = 8\) qui est plus grand que \( r^2 = 4\). Donc le point \( P_3 \) est à l’extérieur du cercle.
Le cercle et les trois points sont indiqués ci-dessous et nous pouvons facilement vérifier la réponse trouvée ci-dessus.

Ligne tangente à un cercle
L'une des propriétés importantes d'une ligne tangente à un cercle est qu'elle est perpendiculaire à la ligne passant par le centre \( C \) et le point de tangence \( M \), comme indiqué ci-dessous.

Exemple 3 Equation d'un cercle et de points à l'intérieur, à l'extérieur ou sur le cercle
Trouvez l'équation de la tangente au cercle avec l'équation \( (x + 2)^2 + (y - 2)^2 = 5 \) au point \( M(-4, 3) \).
Solution de l'exemple 3
En comparant l'équation donnée à l'équation standard générale donnée ci-dessus, nous en déduisons que le centre est en \( C(-2,2) \).
La pente \( m_1 \) de la droite passant par \( C M \) est donnée par
\( m_1 = \dfrac{3-2}{-4-(-2)} = -\dfrac{1}{2} \)
Soit \( m_2 \) la pente de la tangente. Puisque la tangente et \( C M \) sont perpendiculaires, les pentes \( m_1 \) et \( m_2 \) sont liées par
\( m_1 \times m_2 = -1 \)
qui donne
\( (-\dfrac{1}{2}) \times m_2 = -1 \)
résoudre pour \( m_2 \) pour obtenir
\( m_2 = 2 \)
nous connaissons maintenant la pente \( m_2 \) et \( M(-4,3) \) le point de tangence par lequel passe la ligne tangente, nous utilisons la formule de pente du point pour trouver l'équation de la ligne tangente à la donnée cercle
\( y - 3 = 2 (x - (-4)) \)
\( y = 2 x + 11 \)
A titre d'exercice, tracez le cercle donné et l'équation de la tangente trouvée ci-dessus et vérifiez graphiquement qu'ils sont tangents au point (-4,3).
Forme générale de l'équation d'un cercle
Commençons par l'équation standard d'un cercle
\( (x - h)^2 + (y - k)^2 = r^2 \)
Développer
\(x^2 - 2 h x + h^2 + y^2 - 2 k y + k^2 = r^2 \)
Laisser
\( A = - 2 h\), \( B = - 2 k \) et \( C = h^2 + k^2 - r^2\)
Remplacez dans l'équation développée pour obtenir la forme générale de l'équatine d'un cercle.
\(x^2 + y^2 + A x + B y + C = 0 \)
Exemple 4 Trouver l'équation d'un cercle étant donné trois points
Trouvez l'équation du cercle passant par les points \( P_1(6,4) \), \( P_2(-1,5) \) et \( P_3(2,-4) \).
Solution de l'exemple 4
Les coordonnées d'un point sur un cercle doivent satisfaire à l'équation du cercle. On écrit que les coordonnées de chacun des points donnés satisfont l'équation du cercle sous la forme générale : \( x^2 + y^2 + A x + B y + C = 0 \).
Le point \( P_1(6,4) \) est sur le cercle ; remplacer \( x \) par \( 6 \) et \( y \) par \( 4 \) dans l'équation, donc : \( 6^2 + 4^2 + 6 A + 4 B + C = 0 \ )
Le point \( P_2(-1,5) \) est sur le cercle ; remplacer \( x \) par \( -1 \) et \( y \) par \( 5 \) dans l'équation, donc : \( (-1)^2 + 5^2 - A + 5 B + C = 0 \)
Le point \( P_3(2,-4) \) est sur le cercle ; remplacer \( x \) par \( 2 \) et \( y \) par \( -4 \) dans l'équation, d'où : \( 2^2 + (-4)^2 + 2 A - 4 B + C = 0\)
Résoudre le pour (A,B,C) le système d'équations obtenu ci-dessus et présenté ci-dessous sous forme standard
\( \begin{cases} 6 A + 4 B + C = -52\\ - A + 5 B + C = - 26 \\ 2 A - 4 B + C = -20 \end{cases} \)
Utilisez n’importe quelle méthode pour obtenir la solution
\( A = -4\) , \( B = -2 \), \( C = -20 \)
Nous remplaçons maintenant \( A \), \( B \) et \( C \) par leurs valeurs et écrivons l'équation du cercle comme suit :
\(x^2 + y^2 - 4 x - 2 y - 20 = 0 \)
Le cercle trouvé ci-dessus et les trois points sont représentés dans le graphique ci-dessous.

Exemple 5 Réécrivez l'équation générale d'un cercle sous forme standard.
Réécrivez l'équation du cercle donnée par \( x^2 + y^2 + 6x - 2y + 5 = 0 \) et trouvez son centre et son rayon.
Solution de l'exemple 5
Mettez, entre parenthèses, les termes de \( x\) et \( x^2 \) ensemble et les termes de \( y \) et \( y^2\) ensemble
\( (x^2 + 6x) + (y^2 - 2y) + 5 = 0 \)
compléter le carré de chaque binôme entre les parehthèses
\( (x^2 + 3)^2 - 3^2 + (y^2 - 1)^2 - (-1)^2 + 5 = 0 \)
Écrire sous forme standard
\( (x + 3)^2 + (y - 1)^2 = 5 \)
Comparez l'équation ci-dessus à l'équation standard \( (x - h)^2 + (y - k)^2 = r^2\) et identifiez les coordonnées \( h \) et \( k \) du centre de le cercle et le rayon \( r \).
\( h = - 3\) , \( k = 1\) et \( r^2 = 5 \)
Le centre du cercle a les coordonnées : \( (-3 , 1) \) et le rayon \( r = \sqrt 5 \)
D'autres tutoriels sur l'équation du cercle sont inclus dans ce site.
Tutoriels interactifs pour explorer l'équation d'un cercle
L'exploration s'effectue en modifiant les paramètres h, k et r inclus dans l'équation standard \( (x - h)^2 + (y - k)^2 = r^2\).
Il s'agit d'une application HTML5 permettant d'explorer l'équation d'un cercle et les propriétés du cercle.
1 - cliquez sur le bouton au dessus "dessiner" pour commencer. Utilisez les boutons + et - dans le panneau de gauche pour effectuer un zoom avant et arrière.
2 - Utilisez les curseurs et/ou les zones de saisie pour définir les paramètres h et k à zéro et le paramètre r à 1. Vérifiez que le cercle affiché a le centre à (0,0) et le rayon égal à 1.
3 - Cas particulier : Utilisez les curseurs et/ou les cases de saisie pour mettre r à zéro et les paramètres h et k à des valeurs différentes, le graphique du cercle est un point, Expliquez.
(Indice : résolvez l'équation \( (x - h)^2 + (y - k)^2 = 0^2\))
4 - Gardez r égal à 1 et déplacez le cercle en changeant h et k. Vérifiez que le centre du cercle est en (h , k).
5 - Gardez h et k constants et modifiez r. Vérifiez que le cercle a un rayon r.
6 - Réglez h, k et r sur 1. Le cercle a un point d'intersection avec l'axe des x et un point d'intersection avec l'axe des y. C'est ce qu'on appelle les interceptions x et y. Trouvez ces points analytiquement en utilisant l'équation du cercle.
\[ (x - h)^2 + (y - k)^2 = r^2\]
(Indice : pour trouver les interceptions $x$, définissez y = 0 dans l'équation et résolvez x. Pour trouver les ordonnées à l'origine, définissez x = 0 dans l'équation et résolvez y.)
7- Réglez r à 2 et h à une certaine valeur. Changez k de -1,8 à 1,8 (|h| < r). Combien y a-t-il d’ordonnées à l’origine x ? Réglez k sur 2 (le rayon). Combien y a-t-il d'intersections x ? Réglez k sur -2, combien y a-t-il d’intersections x ? Fixez k à des valeurs supérieures à 2 (le rayon), combien y a-t-il d'intersections x ? Définissez k sur des valeurs inférieures à -2, combien y a-t-il d'intersections x ? Expliquez de manière analytique.
8- Essayez la même exploration qu'en 7 ci-dessus avec les ordonnées à l'origine en changeant la valeur de h.
9- Exercice : Trouver (analytiquement) les valeurs de h, k et r telles que le cercle associé à ces valeurs n'a pas d'ordonnée à l'origine x ou y. Vérifiez votre réponse graphiquement.
Références et liens
Feuilles d'exercices mathématiques étape par étape Solveurs
Trouver les coordonnées à l'origine x et y des cercles - Calculatrice
Tutoriel sur l'équation du cercle
Problèmes mathématiques et autotests en ligne.
Page d'accueil

 Pour trouver l'équation, on utilise la définition pour écrire que la distance CM est égale au rayon r
Pour trouver l'équation, on utilise la définition pour écrire que la distance CM est égale au rayon r
 Travailler avec la racine carrée ajoute des difficultés supplémentaires qui peuvent être évitées. La racine carrée de l'équation ci-dessus peut être éliminée en mettant au carré les deux côtés de l'équation pour obtenir
Travailler avec la racine carrée ajoute des difficultés supplémentaires qui peuvent être évitées. La racine carrée de l'équation ci-dessus peut être éliminée en mettant au carré les deux côtés de l'équation pour obtenir
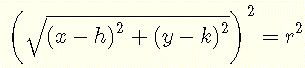 Simplifiez pour obtenir l'équation standard d'un cercle de centre C(h,k) et de rayon r
Simplifiez pour obtenir l'équation standard d'un cercle de centre C(h,k) et de rayon r


